- 2021-06-20 发布 |
- 37.5 KB |
- 7页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高考数学专题复习:《导数及其应用》单元测试题5
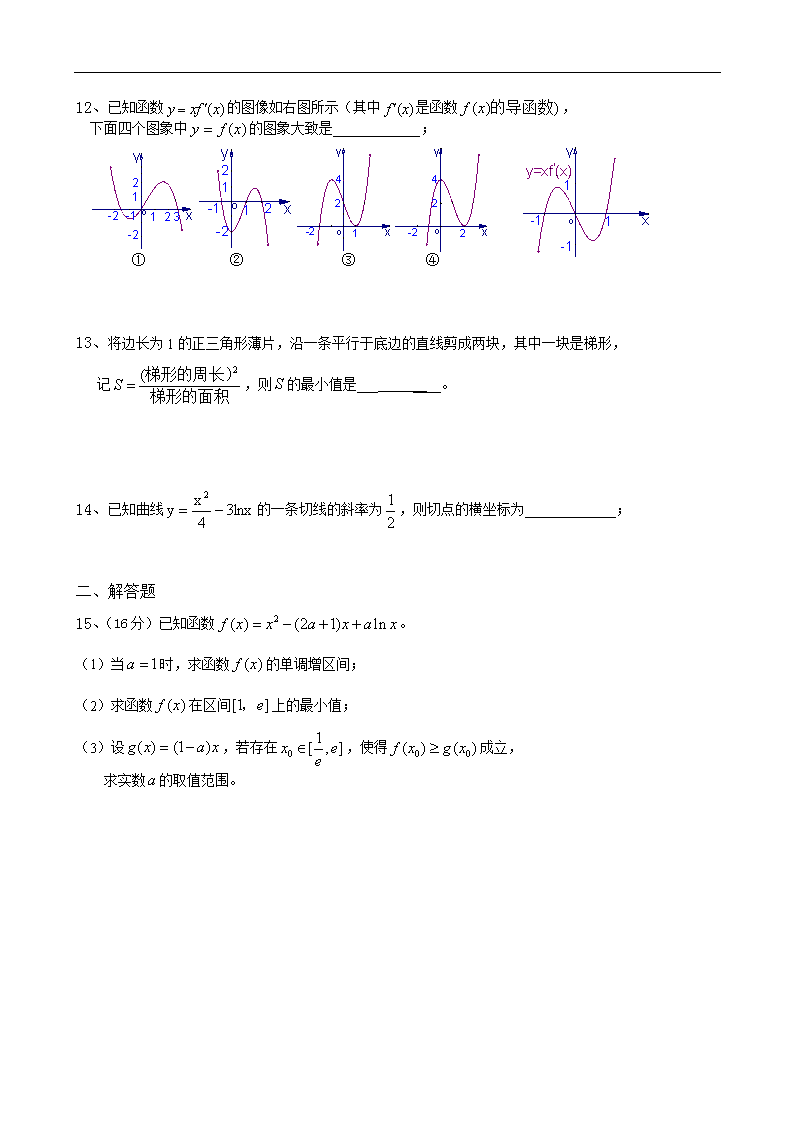
《导数及其应用》单元测试题5 一、填空题 1、已知函数在区间上的最大值与最小值分别为, 则___________; 2、曲线在点处的切线斜率_________ ___; 3、函数的单调减区间为_________ __ _____; 4、设,若,则__________ ______; 5、函数的极大值是___________; 6、曲线在点处的切线方程是________________; 7、函数,已知在时取得极值,则=_______ __; 8、设曲线在点(1,)处的切线与直线平行,则____________; 9、函数的导数 ; 10、曲线在点处的切线与x轴、直线所围成的三角形的面积为 ; 11、设曲线在点处的切线与直线垂直,则 ; 12、已知函数的图像如右图所示(其中是函数, 下面四个图象中的图象大致是______ ______; ① ② ③ ④ 13、将边长为1的正三角形薄片,沿一条平行于底边的直线剪成两块,其中一块是梯形, 记,则的最小值是___ ____。 14、已知曲线的一条切线的斜率为,则切点的横坐标为_____________; 二、解答题 15、(16分)已知函数。 (1)当时,求函数的单调增区间; (2)求函数在区间上的最小值; (3)设,若存在,使得成立, 求实数的取值范围。 16、(14分)已知函数。 (1)求函数的单调递减区间; (2)若函数在区间[-2,2]上的最大值为20,求它在该区间上的最小值。 17、(14分)设函数,已知是奇函数。 (1)求、的值。 (2)求函数的单调区间与极值。 18、(15分)已知函数的图象过点,且在点 处的切线方程为. (1)求函数的解析式; (2)求函数在区间上的最值。 19、(15分)用长为18 m的钢条围成一个长方体形状的框架,要求长方体的长与宽之比 为2:1,问该长方体的长、宽、高各为多少时,其体积最大?最大体积是多少? 20、(16分)设,函数。 (1)若是函数的极值点,求的值; (2)若函数,在处取得最大值,求的取值范围。 以下是答案 一、填空题 1、32 2、1 3、_ 4、 5、2 6、 7、5 8、1 9、 10、 11、2 12、③ ① ② ③ ④ 13、 14、3 二、解答题 15、解:(1)单调增区间 (2)当时,; 当时,; 当时, (3) 16、解:(1)单调减区间 (2)-7 17、解:(1), (2)单调增区间 单调减区间 当时,取极大值, 当时,取极大值, 18、解:(1) (2)最大值,最小值-43. 19、解:当长为2 m,宽为1 m,高为1.5 m时,体积最大,最大体积为3 m3 20、解:(1)1; (2)查看更多