- 2021-06-20 发布 |
- 37.5 KB |
- 6页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
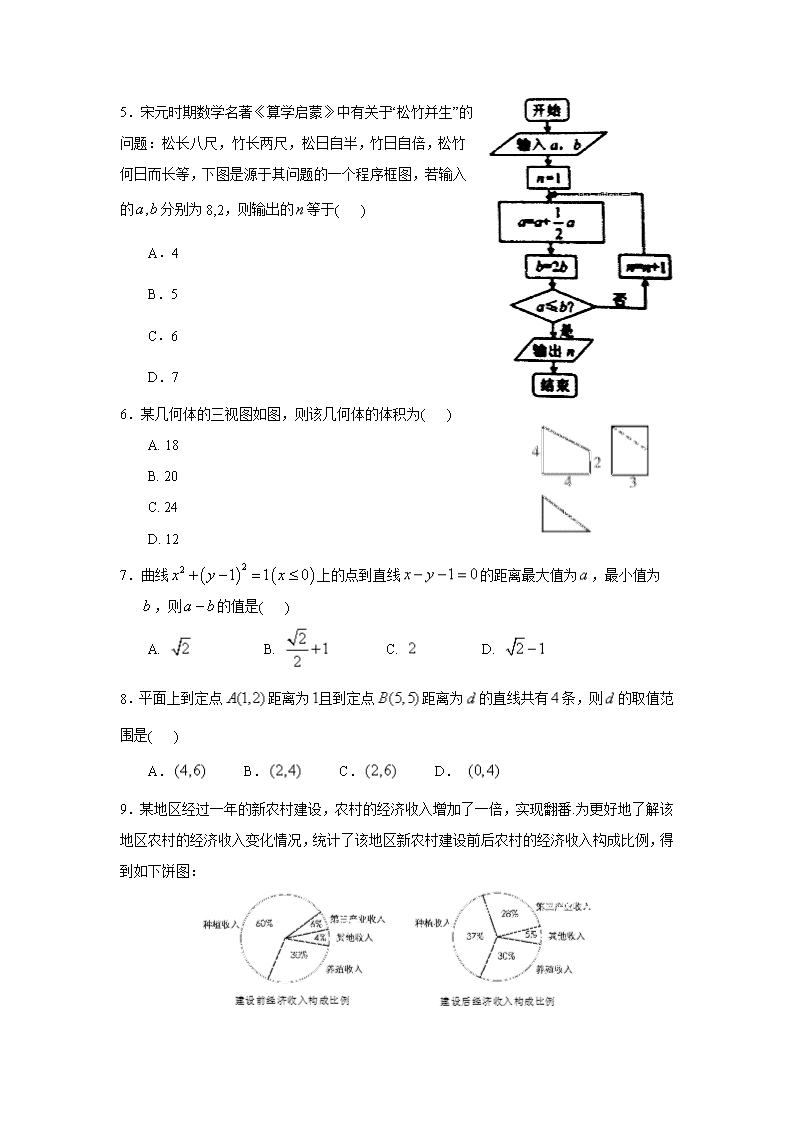
湖北省黄陂六中2018-2019学年高二上学期武汉市部分学校10月月考数学试卷+Word版缺答案
武汉市部分学校高二年级10月考 数学试题 ★祝考试顺利★ 考试时间:120分钟 满分:150分 注意事项: 1.答卷前,考生务必将自己的姓名、考号、班级填写在试题卷和答题卷上。 2.选择题的作答:每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。答在试题卷、草稿纸上无效。 3.非选择题作答:用签字笔直接答在答题卡上对应的答题区域内。答在试题卷、草稿纸上无效。 4.考生必须保持答题卡的整洁。考试结束后,请将答题卡上交。 一、选择题(每小题5分) 1.为了适应新高考改革,尽快推行不分文理教学,对比学生考试情况,采用分层抽样的方法从文科生900人,理科生1800人,教师人中抽取150人进行问卷分析,已知文科生抽取的人数为45人,那么教师被抽取的人数为( ) A.12人 B.15人 C.21人 D.24人 2.若直线l1和l2是异面直线,l1在平面α内,l2在平面β内,l是平面α与平面β的交线,则下列命题正确的是( ) A.l与l1,l2都不相交 B. l与l1,l2都相交 C.l至多与l1,l2中的一条相交 D.l至少与l1,l2中的一条相交 3.若下面框图所给的程序运行结果为,那么判断框中应填入的关于的条件是( ) A. B. C. D. 4.直线l经过A(2,1),B(1,m2)(m∈R)两点,那么直线l的倾斜角α的取值范围是( ). A. B. C. D. 5.宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题:松长八尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等,下图是源于其问题的一个程序框图,若输入的分别为8,2,则输出的等于( ) A.4 B.5 C.6 D.7 6.某几何体的三视图如图,则该几何体的体积为( ) A. 18 B. 20 C. 24 D. 12 7.曲线上的点到直线的距离最大值为,最小值为,则的值是( ) A. B. C. D. 8.平面上到定点距离为且到定点距离为的直线共有条,则的取值范围是( ) A. B. C. D. 9.某地区经过一年的新农村建设,农村的经济收入增加了一倍,实现翻番.为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例,得到如下饼图: 则下面结论中不正确的是( ) A.新农村建设后,种植收入减少 B.新农村建设后,其他收入增加了一倍以上 C.新农村建设后,养殖收入增加了一倍 D.新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半 10.已知实数、满足条件,则的最大值为( ) A. B. C. D.1 11.若直线始终平分圆: 的的周长,则的最小值为( ) A. B. 5 C. D. 10 12.若关于的方程有且只有两个不同的实数根,则实数的取值范围是 A. B. C. D. 二、填空题(每小题5分) 13.过点P(1,2),并且在两轴上的截距互为相反数的直线方程是__________. 14.为了解某地区某种农产品的年产量(单位:吨)对价格(单位:千元/吨)的影响,对近五年该农产品的年产量和价格统计如下表: 1 2 3 4 5 7.0 6.5 3.8 2.2 已知和具有线性相关关系,且回归方程为,那么表中的值为 . 15.已知,直线:和直线:分别与圆:相交于、和、,则四边形的面积为 . 16.已知圆C1:x2+y2-2ax+a2-9=0 和圆C2:x2+y2+2by-4+b2=0恰有三条公切线,若a∈R,b∈,令t=a+b,则t的取值范围是_________. 三、解答题(共6小题,解答应写出相应的文字说明、证明过程或演算步骤). 17.(10分)在平行四边形ABCD中,A(1,1)、B(7,3)、D(4,6),点M是线段AB的中点线段CM与BD交于点P. (1)求直线CM的方程; (2)求点P的坐标. 18.(12分)某种产品的广告费支出x与销售额y(单位:万元)之间有如下对应数据: x 2 4 5 6 8 y 30 40 60 50 70 (1)若用线性回归模型拟合y与x的关系,请用相关系数说明拟合效果; (2)求线性回归方程,并预测广告费支出为10万元时,销售额为多大? 附: ≈1.414 相关系数: r= 回归方程为=x+,其中 19.(12分)如图,四边形为正方形,分别为的中点,以为折痕把折起,使点到达点的位置,且. (1)证明:平面平面; (2)求与平面所成角的正弦值. 20.(12分)在平面直角坐标系xoy中,曲线与坐标轴的交点都在圆C上. (1)求圆C的方程; (2)若圆C与直线交于A,B两点,且OA⊥OB,求a的值. 21.(12分)某市政府为了节约生活用电,计划在本市试行居民生活用电定额管理,即确定一个居民月用电量标准,用电量不超过的部分按平价收费,超出的部分按议价收费.为此,政府调查了100户居民的月平均用电量(单位:度),以,,,,,,分组的频率分布直方图如图所示. (1)求直方图中的值; (2)求月平均用电量的众数和中位数; (3)如果当地政府希望使左右的居民每月的用电量不超出标准,根据样本估计总体的思想,你认为月用电量标准应该定为多少合理? 22.(12分)已知直线l:4x+3y+10=0,半径为2的圆C与l相切,圆心C在x轴上且在直线l的右上方. (1)求圆C的方程; (2)过点M(1,0)的直线与圆C交于A,B两点(A在x轴上方),问在x轴正半轴上是否存在定点N,使得x轴平分∠ANB?若存在,请求出点N的坐标;若不存在,请说明理由.查看更多