2014高一数学（人教A版）必修2能力强化提升：1-3-2 球的体积和表面积

2014高一数学（人教A版）必修2能力强化提升：1-3-2 球的体积和表面积

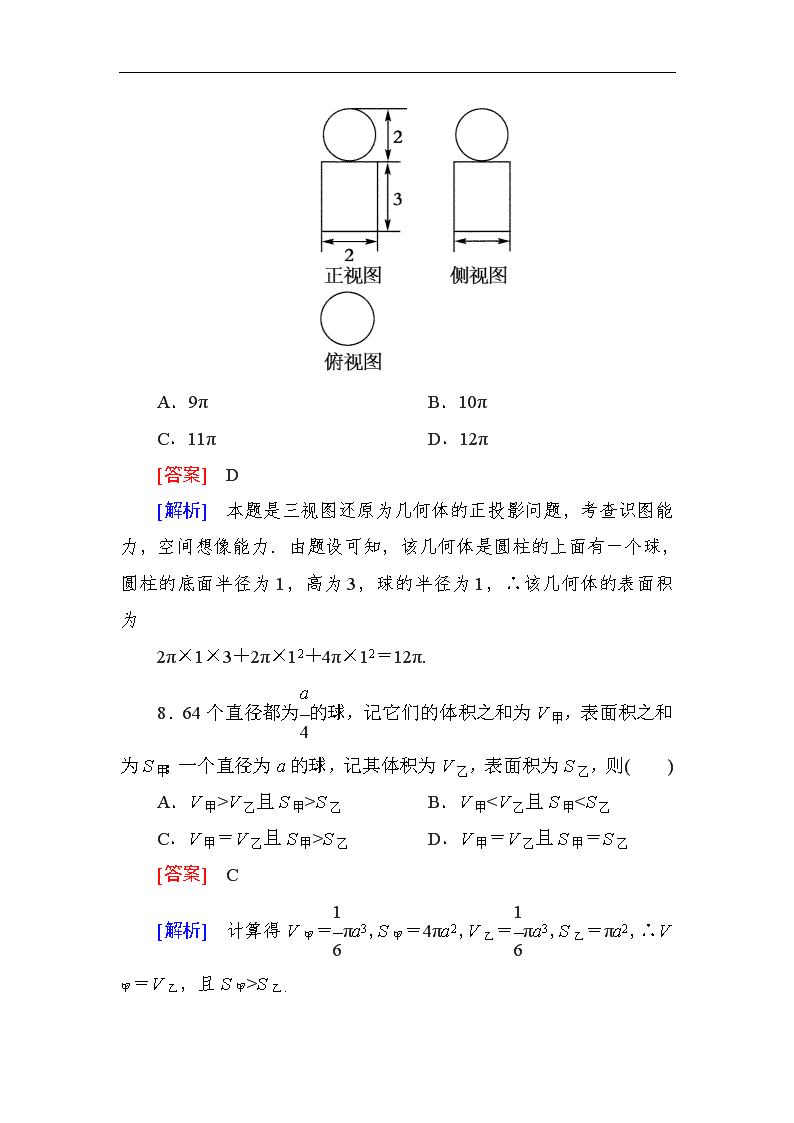
一、选择题 ‎1．球的体积与其表面积的数值相等，则球的半径等于 (　　)‎ A.　　　　B．‎1　‎　　　C．2　　　　D．3‎ ‎[答案]　D ‎2．半径为R的球内接一个正方体，则该正方体的体积是(　　)‎ A．2R3 B.πR3‎ C.R3 D.R3‎ ‎[答案]　C ‎3．把3个半径为R的铁球熔成一个底面半径为R的圆柱，则圆柱的高为(　　)‎ A．R B．2R C．3R D．4R ‎[答案]　D ‎4．一个正方体与一个球表面积相等，那么它们的体积比是(　　)‎ A. B. C. D. ‎[答案]　A ‎[解析]　由‎6a2＝4πR2得＝，∴＝＝3＝.‎ ‎5．已知轴截面是正方形的圆柱的高与球的直径相等，则圆柱的全面积与球的表面积的比是(　　)‎ A．6:5 B．5:4‎ C．4:3 D．3:2‎ ‎[答案]　D ‎[解析]　设球的半径为R，则圆柱的高h＝2R，底面的半径也为R，∴＝＝.‎ ‎6．(2012～2013山东临清中学高一第三次月考试题)已知长方体一个顶点上三条棱的长分别是3、4、5，且它的顶点都在同一球面上，则这个球的表面积是(　　)‎ A．20 B．25 C．50π D．200π ‎[答案]　C ‎[解析]　长方体的体对角线即为球的直径，∴2R＝，∴R＝，S球＝4πR2＝50π.‎ ‎7．下图是一个几何体的三视图，根据图中数据，可得该几何体的表面积是(　　)‎ A．9π B．10π C．11π D．12π ‎[答案]　D ‎[解析]　本题是三视图还原为几何体的正投影问题，考查识图能力，空间想像能力．由题设可知，该几何体是圆柱的上面有一个球，圆柱的底面半径为1，高为3，球的半径为1，∴该几何体的表面积为 ‎2π×1×3＋2π×12＋4π×12＝12π.‎ ‎8．64个直径都为的球，记它们的体积之和为V甲，表面积之和为S甲；一个直径为a的球，记其体积为V乙，表面积为S乙，则(　　)‎ A．V甲>V乙且S甲>S乙 B．V甲S乙 D．V甲＝V乙且S甲＝S乙 ‎[答案]　C ‎[解析]　计算得V甲＝πa3，S甲＝4πa2，V乙＝πa3，S乙＝πa2，∴V甲＝V乙，且S甲>S乙．‎ 二、填空题 ‎9．用过球心的平面将一个球平均分成两个半球，则两个半球的表面积和是原来整球表面积的________倍．‎ ‎[答案]　 ‎[解析]　S球＝4πR2,2S半＝(2πR2＋πR2)×2＝6πR2，‎ ＝＝.‎ ‎10．若圆柱、圆锥的底面直径和高都等于球的直径，则圆柱、圆锥、球的体积的比为________．‎ ‎[答案]　3:1:2‎ ‎[解析]　V柱＝πR2×2R＝2πR3，‎ V锥＝πR2×2R＝R3，‎ V球＝πR3.‎ V柱:V锥:V球＝3:1:2.‎ ‎11．已知棱长为2的正方体的体积与球O的体积相等，则球O的半径为________．‎ ‎[答案]　 ‎[解析]　设球O的半径为r，则πr3＝23，‎ 解得r＝ ‎12．(2010·湖北高考)圆柱形容器内盛有高度为‎8 cm的水，若放入三个相同的球(球的半径与圆柱的底面半径相同)后，水恰好淹没最上面的球(如图所示)，则球的半径是________cm.‎ ‎[答案]　4‎ ‎[解析]　设球的半径为r，则圆柱形容器的高为6r，容积为πr2×6r＝6πr3，高度为‎8 cm的水的体积为8πr2,3个球的体积和为3×πr3＝4πr3，由题意6πr3－8πr2＝4πr3，解得r＝4.‎ 三、解答题 ‎13．(2012～2013·福建厦门高一检测)如图是一个几何体的三视图，根据图中数据，求该几何体的表面积和体积．‎ ‎[解析]由三视图可知此几何体是半径为2的半球．‎ S＝×4πR2＋πR2＝12π，‎ V＝πR3×＝π.‎ ‎14．一试管的上部为圆柱形，底部为与圆柱底面半径相同的半球形．圆柱形部分的高为h cm，半径为r cm.试管的容量为108π cm3，半球部分容量为全试管容量的.‎ ‎(1)求r和h；‎ ‎(2)若将试管垂直放置，并注水至水面离管口‎4 cm处，求水的体积．‎ ‎[解析]　(1)∵半球部分容量为全试管容量的，‎ ‎∴半球部分与圆柱体部分容量比为，‎ 即＝ ‎∴h＝r，πr3×＝108π× ‎∴r＝3(cm)，h＝10(cm)．‎ ‎(2)V＝πr3×＋πr2×(h－4)‎ ‎＝π×33×＋π×32×6＝72π(cm3)．‎ ‎15．体积相等的正方体、球、等边圆柱(轴截面为正方形)的全面积分别是S1、S2、S3，试比较它们的大小．‎ ‎[解析]　设正方体的棱长为a，球的半径为R，等边圆柱的底面半径为r，则S1＝‎6a2，S2＝4πR2，S3＝6πr2.‎ 由题意知，πR3＝a3＝πr2·2r，‎ ‎∴R＝a，r＝a，‎ ‎∴S2＝4π2＝4π·a2＝a2，‎ S3＝6π2＝6π·a2＝a2，‎ ‎∴S2‎3a2＝a2，即S1>S3.‎ ‎∴S1、S2、S3的大小关系是S2

查看更多