数学（职教班）卷·2019届河北省衡水市安平中学高二上学期第二次月考（2017-10）

数学（职教班）卷·2019届河北省衡水市安平中学高二上学期第二次月考（2017-10）

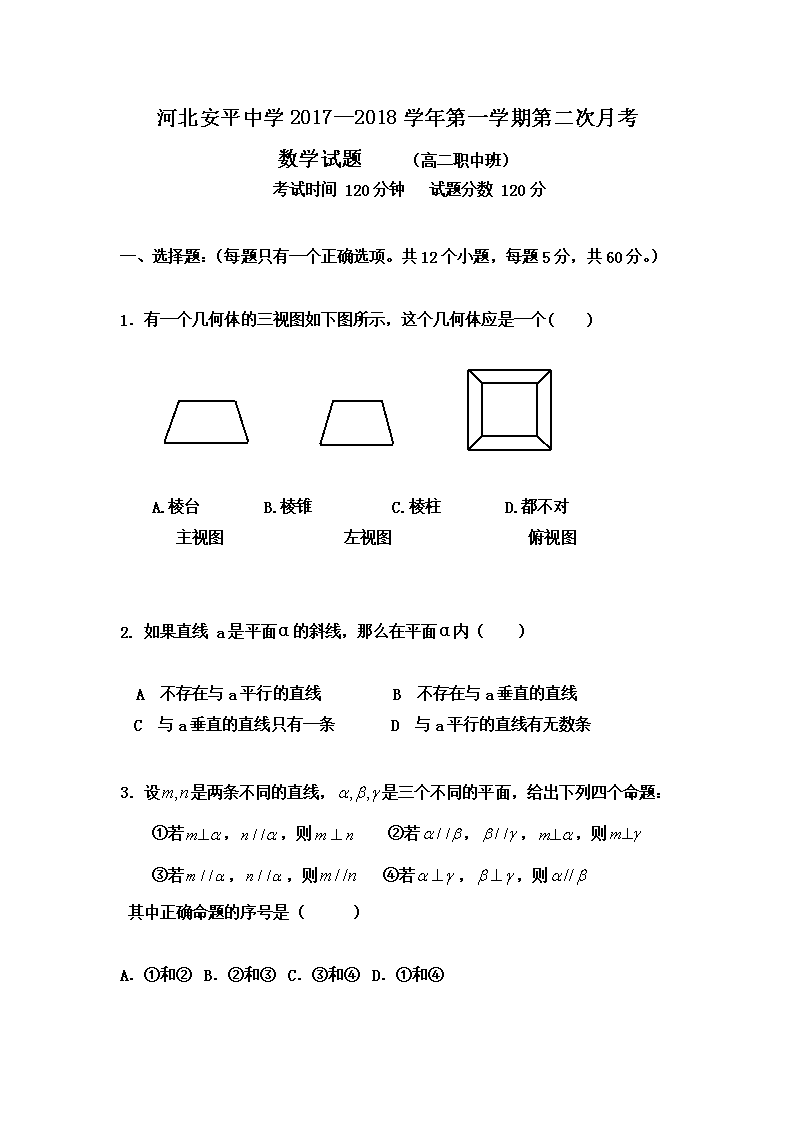
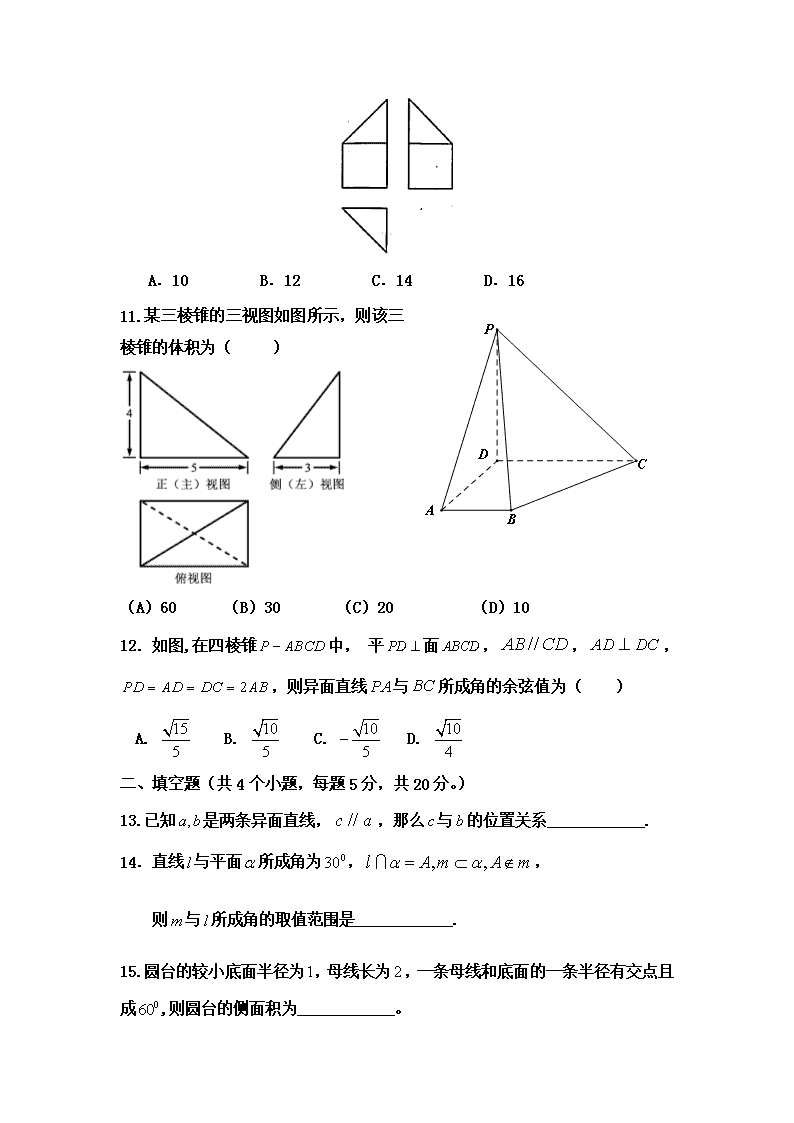
河北安平中学2017—2018学年第一学期第二次月考 数学试题 （高二职中班）‎ 考试时间 120分钟 试题分数 120分 ‎ ‎ ‎ 一、 选择题：（每题只有一个正确选项。共12个小题，每题5分，共60分。）【来源：全,品…中&高*考+网】‎ ‎1．有一个几何体的三视图如下图所示，这个几何体应是一个( )‎ A.棱台 B.棱锥 C.棱柱 D.都不对 ‎ 主视图 左视图 俯视图 2. 如果直线 a是平面α的斜线，那么在平面α内（ ）‎ ‎ A 不存在与a平行的直线 B 不存在与a垂直的直线 C 与a垂直的直线只有一条 D 与a平行的直线有无数条 ‎3．设是两条不同的直线，是三个不同的平面，给出下列四个命题：‎ ‎ ①若，，则 ②若，，，则 ‎ ③若，，则 ④若，，则 ‎ 其中正确命题的序号是 ( )‎ A． ‎①和② B．②和③ C．③和④ D．①和④‎ ‎ 4．若平面α外两直线a,b在α上的射影是两相交直线，则a与b的位置关系是（ ）‎ ‎ A 相交 B 相交或异面 C 异面 D 相交或平行 ‎ 主视图 左视图 俯视图 ‎5．如果一个水平放置的图形的斜二测直观图是一个底面为，‎ 腰和上底均为的等腰梯形，那么原平面图形的面积是（ ）‎ A． B． C． D． ‎ ‎6．已知直线，与平面，下列命题正确的是（ ）【来源：全,品…中&高*考+网】‎ A、若//，，则// B、若//，//，则//‎ C、若//，，则// D、若//，，则//或 7． 一个正方体的顶点都在球面上，它的棱长为，则球的表面积是（　 　）‎ Ａ．　　Ｂ．　　Ｃ．　　 Ｄ．‎ 8. 正四棱锥的侧棱长与底面边长都是1，则侧棱与底面所成的角为（ ）‎ A. B. C. D. ‎ ‎9．棱长都是的三棱锥的表面积为（ ）‎ A. B. C. D. ‎ ‎10．某多面体的三视图如图所示，其中正视图和左视图都由正方形和等腰直角三角形组成，正方形的边长为2，俯视图为等腰直角三角形.该多面体的各个面中有若干个是梯形，这些梯形的面积之和为（ ）‎ A．10 B．‎12 ‎ C．14 D．16‎ ‎11.某三棱锥的三视图如图所示，则该三棱锥的体积为（ ）‎ ‎（A）60 （B）30 （C）20 （D）10‎ ‎12．如图,在四棱锥中， 平面，，，，则异面直线与所成角的余弦值为（ ）‎ A. B. C. D. ‎ 二、填空题（共4个小题，每题5分，共20分。）‎ ‎13.已知是两条异面直线，，那么与的位置关系____________.‎ ‎14．直线与平面所成角为，，‎ 则与所成角的取值范围是____________.‎ ‎15.圆台的较小底面半径为，母线长为，一条母线和底面的一条半径有交点且成,则圆台的侧面积为____________。 ‎ ‎16．下列命题中：‎ ‎（1）、平行于同一直线的两个平面平行；‎ ‎（2）、平行于同一平面的两个平面平行；‎ ‎（3）、垂直于同一直线的两直线平行；‎ ‎（4）、垂直于同一平面的两直线平行. 其中正确的个数有_____________。‎ 三、 解答题：（解答题应写出必要的文字说明和演算步骤）‎ ‎17．已知为空间四边形的边上的点，且．求证：. ‎ ‎18． 如图：是平行四边形平面外一点，分别是上的点，且= ， 求证：平面.‎ ‎19.如图，在四棱锥P-ABCD中，AB//CD，且．‎ ‎（1）证明：平面PAB⊥平面PAD；‎ ‎（2）若PA=PD=AB=DC，，且四棱锥P-ABCD的体积为，求该四棱锥的侧面积．‎ ‎20．（本小题12分）在如图所示的四棱锥 中，已知 PA⊥平面ABCD，‎ ‎，，，为的中．‎ ‎（Ⅰ）求证：MC∥平面PAD； ‎ ‎（Ⅱ）求证：平面PAC⊥平面PBC.‎ ‎ ‎ 数学答案 （高二职中班）‎ 选择题 AAABA DBCAB DB 填空题 13.异面或相交 14. 15. 16.‎ 解答题 ‎　17、(本题满分10分)‎ 证明：‎ ‎18、(本题满分10分)‎ ‎19.(本题满分10分)　【来源：全,品…中&高*考+网】‎ ‎（2）在平面内作，垂足为．‎ 由（1）知，平面，故，可得平面．‎ 设，则由已知可得，．【来源：全,品…中&高*考+网】‎ 故四棱锥的体积．‎ 由题设得，故．‎ 从而，，．‎ 可得四棱锥的侧面积为．‎ ‎20.(本题满分10分)‎ 解：（Ⅰ ）如图，取PA的中点E，连接ME，DE，∵M为PB的中点，‎ ‎∴EM//AB,且EM= AB. 又∵，且，‎ ‎∴EM//DC，且EM=DC ∴四边形DCME为平行四边形, ‎ 则MC∥DE，又平面PAD, 平面PAD 所以MC∥平面PAD ‎ ‎（Ⅱ）∵PA⊥平面ABCD，∴PA⊥BC ，‎ 又,∴BC⊥平面PAC，又平面PBC,所以，平面PAC⊥平面PBC； ‎ ‎（Ⅲ）取PC中点N，则MN∥BC 由（Ⅱ）知BC⊥平面PAC，则MN⊥平面PAC 所以，为直线MC与平面PAC所成角，‎ ‎， 【来源：全,品…中&高*考+网】‎ ‎ ‎