- 2021-06-19 发布 |
- 37.5 KB |
- 9页

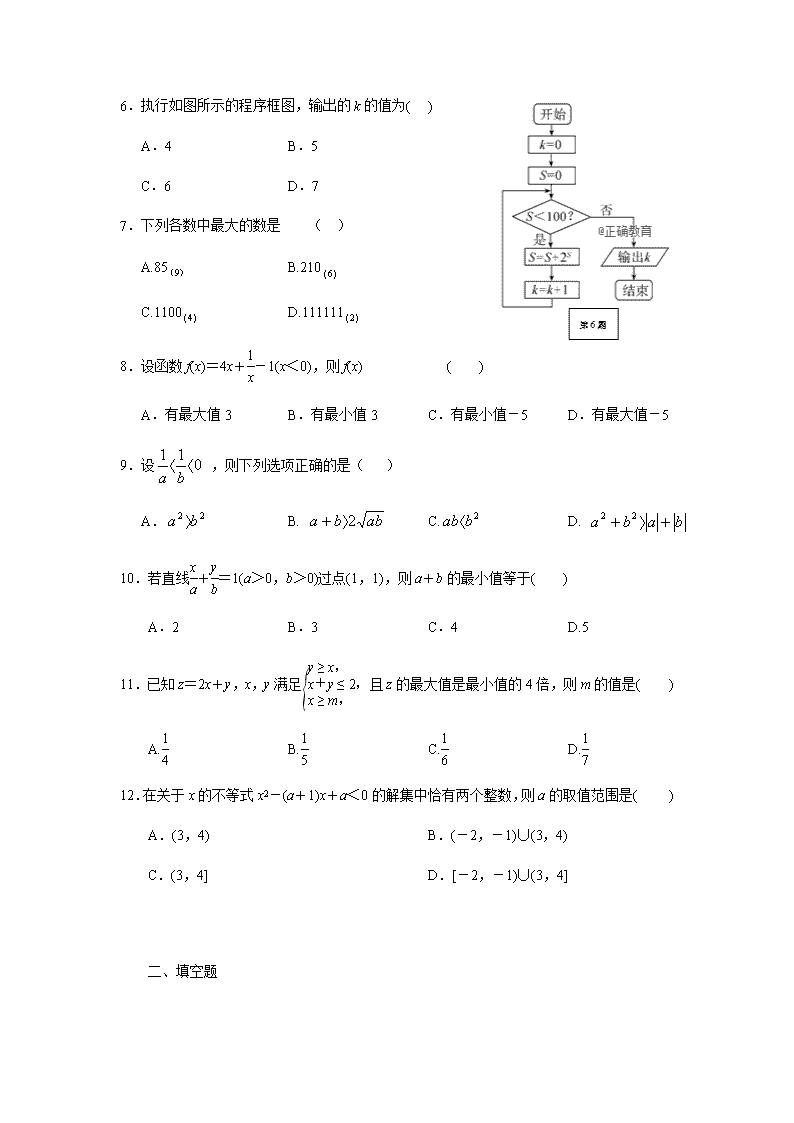

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2018-2019学年甘肃省张掖二中高二上学期10月月考数学试题(英才、育才)(Word版)
张掖二中 2018—2019 学年度第一学期月考试卷(10 月) 高二数学(英才、育才) 命题人:张志霞 1.一个年级有 12 个班,每个班有 50 名同学,随机编号为 1~50 号,为了了解他们在课外 的兴趣爱好,要求每班的 33 号学生留下来参加阅卷调查,这里运用的抽样方法是( ) A.分层抽样法 B.抽签法 C.随机数表法 D.系统抽样法 2、若角α,β满足-π 2 <α<β<π,则α-β的取值范围是( ) A. -3π 2 ,3π 2 B. -3π 2 ,0 C. 0,3π 2 D. -π 2 ,0 3.函数 f(x)=log2(x2+2x-3)的定义域是( ) A.[-3,1] B.(-3,1) C.(-∞,-3]∪[1,+∞) D.(-∞,-3)∪(1,+∞) 4.阅读如图所示的程序框图,运行相应的程序,若输入 x 的值为 1, 则输出 y 的值为( ) A.2 B.7 C.8 D.128 5.已知集合 P={x|x2-2x≥0},Q={x|1<x≤2},则 ∩Q=( ) A.[0,1) B.(0,2] C.(1,2) D.[1,2] 6.执行如图所示的程序框图,输出的 k 的值为( ) A.4 B.5 C.6 D.7 7.下列各数中最大的数是 ( ) A.85 )(9 B.210 )6( C.1100 )4( D.111111 )2( 8.设函数 f(x)=4x+1 x -1(x<0),则 f(x) ( ) A.有最大值 3 B.有最小值 3 C.有最小值-5 D.有最大值-5 9.设 011 ba ,则下列选项正确的是( ) A. 22 ba B. abba 2 C. 2bab D. baba 22 10.若直线x a +y b =1(a>0,b>0)过点(1,1),则 a+b 的最小值等于( ) A.2 B.3 C.4 D.5 11.已知 z=2x+y,x,y 满足 y≥x, x+y≤2, x≥m, 且 z 的最大值是最小值的 4 倍,则 m 的值是( ) A.1 4 B.1 5 C.1 6 D.1 7 12.在关于 x 的不等式 x2-(a+1)x+a<0 的解集中恰有两个整数,则 a 的取值范围是( ) A.(3,4) B.(-2,-1)∪(3,4) C.(3,4] D.[-2,-1)∪(3,4] 二、填空题 13.若 ,x y 满足约束条件 0, 2 6, 2, x y x y x y 则 3z x y 的最小值是______。 14.若不等式 ax2-ax-2≤0 的解集是 R ,则 a 的取值范围是 15.已知 x>0,y>0,且2 x +1 y =1,若 x+2y>m2+2m 恒成立,则实数 m 的取值范围是 . 16.已知 a∈R,函数 2 2 2 2 0 2 2 0 x x a xf x x x a x , , , .若对任意 x∈[–3,+ ),f(x)≤ x 恒成 立,则 a 的取值范围是__________. 三、解答题 17.各项都为正数的等比数列 na 中, 1 5 31 4a a a , . (1)求 na 的通项公式; (2)记 nS 为 na 的前 n项和.若 63mS ,求 m . 18.在△ABC 中,角 A,B,C 的对边分别为 a,b,c.已知 CBCB coscos41)cos(2 (1)求角 A 的大小; (2)若 72a ,△ABC 的面积为 32 ,求 cb . 19.某车间 20 名工人年龄数据如下表: 年龄(岁) 工人数(人) 19 1 28 3 29 3 30 5 31 4 32 3 40 1 合计 20 (1)求这 20 名工人年龄的众数与极差; (2)以十位数为茎,个位数为叶,作出这 20 名工人年龄的茎叶图; (3)求这 20 名工人年龄的方差. 20.某城市 100 户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220), [220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图. (1) 求直方图中 x 的值; (2) 求月平均用电量的中位数; (3) 在月平均用电量为[220,240),[240,260),[260,280),[280,300]的四组用户中,用分 层抽 样的方法抽取 11 户居民,则月平均用电量在[220,240)的用户中应抽取多少户? 21.某项研究表明:在考虑行车安全的情况下,某路段车流量 F(单位时间内经过测量点的 车辆数,单位:辆/小时)与车流速度 v(假设车辆以相同速度 v 行驶,单位:米/秒)、平 均车长 l(单位:米)的值有关,其公式为 F= 76 000v v2+18v+20l. ①如果不限定车型,l=6.05,则最大车流量为________辆/小时; ②如果限定车型,l=5,则最大车流量比(1)中的最大车流量增加________辆/小时. 22.已知二次函数 ( )f x 满足 ( 1) 0f ,且 21( ) ( 1)2x f x x 对一切实数 x 恒成立. (1) 求 (1)f ; (2) 求 ( )f x 的解析式; (3) 求证: 1 1 2 ( ) 2 n i n f k n ( ).n N 张掖二中 2018—2019 学年度第一学期月考试卷(10 月) 高二数学(英才、育才)答案 1-5:DBDCC 6-10:ACDCC 11-12:AD 13. -2 14. [-8,0] 15. (-4,2) 16.[ 1 8 ,2] 17. 解:(1)设{ }na 的公比为 q ,由题设得 1n na q .由已知得 4 24q q ,解得 0q (舍 去), 2q .故 12n na . (2)由 63mS 得若 12n na ,则 2 1n nS .由 63mS 得 2 64m ,解得 6m .综上, 6m 18. 19.【解】 (1)由题可知,这 20 名工人年龄的众数是 30,极差是 40-19=21. (2)这 20 名工人年龄的茎叶图如图所示: (3)这 20 名工人年龄的平均数为 x = 1 20(19+3×28+3×29+5×30+4×31+3×32+40)= 30, ∴这 20 名工人年龄的方差为 s2= 1 20 20 1i (xi- x )2=112+6×22+7×12+5×02+102 20 =252 20 20.【解】 (1)由(0.002+0.009 5+0.011+0.012 5+x+0.005+0.002 5)×20=1 得: x=0.007 5,所以直方图中 x 的值是 0.007 5. (2)因为(0.002+0.009 5+0.011)×20=0.45<0.5,所以月平均用电量的中位数在[220,240) 内, 设中位数为 a,由(0.002+0.009 5+0.011)×20+0.012 5×(a-220)=0.5 得:a=224,所以月平均用电量的中位数是 224. (3)月平均用电量为[220,240]的用户有 0.012 5×20×100=25 户,月平均用电量为[240,260) 的 用户有 0.007 5×20×100=15 户,月平均用电量为[260,280)的用户有 0.005×20×100=10 户, 月平均用电量为[280,300]的用户有 0.002 5×20×100=5 户,抽取比例= 11 25+15+10+5 = 1 5 , 所以月平均用电量在[220,240)的用户中应抽取 25×1 5 =5 户. 21.【解析】①若 l=6.05,则 F= 76 000v v2+18v+20l = 76 000v v2+18v+121 = 76 000 v+121 v +18 . ∵v>0,∴v+121 v +18≥2 121+18=40,∴F≤76 000 40 =1 900. ②若 l=5,则 F= 76 000v v2+18v+20l = 76 000v v2+18v+100 = 76 000 v+100 v +18 . ∵v>0,∴v+100 v +18≥38,∴F≤76 000 38 =2 000. ∴此时最大车流辆比(1)中的最大车流量增加 100 辆/小时. 22. 解:(1)由已知令 1x 得: 211 (1) (1 1) 12f (1) 1.f (2)令 2( ) ( 0)f x ax bx c a 由 1)1(,0)1( ff 得: 0 1 a b c a b c 1 1,2 2b c a 即 2 1 1( ) 2 2f x ax x a 则 21( ) ( 1)2x f x x 对任意实数 x 恒成立就是 2 2 1 1 02 2 (1 2 ) 2 0 ax x a a x x a 对任意实数恒成立,即: 2 1 2 2 0,1 2 0 1(2 ) 02 (4 1) 0 a a a a 1 1,4 4a c 则 21 1 1( ) 4 2 4f x x x (3)由(2)知 21( ) ( 1)4f x x 故 2 1 4 4 ( ) ( 1)( 2)( 1)f k k kk 1 14( )1 2k k 1 1 1 1 1 1 14(( ) 2 3 3 4 1 n i f k n 1 )2n 2 2 n n 故原不等式成立.查看更多