- 2021-06-19 发布 |
- 37.5 KB |
- 7页

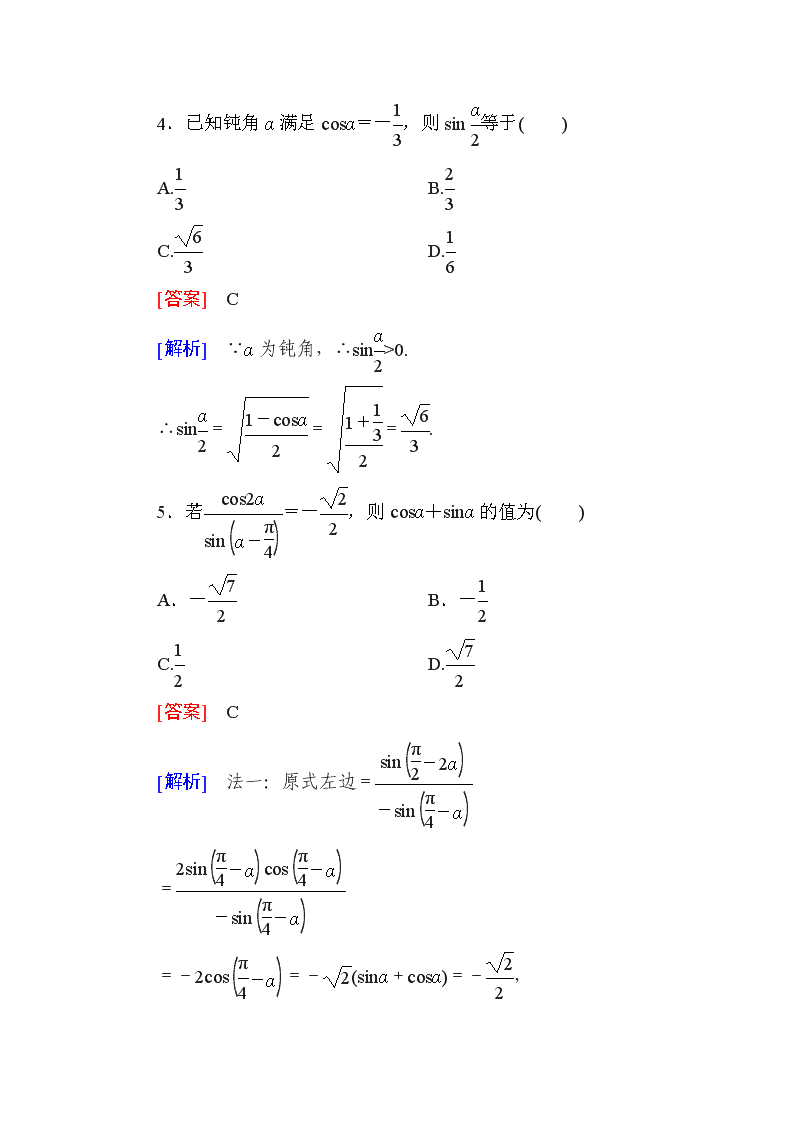

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高一数学(人教A版)必修4能力提升:3-2-1 三角恒等变换
能 力 提 升 一、选择题 1.函数y=sin2xcos2x是( ) A.周期为的奇函数 B.周期为的偶函数 C.周期为的奇函数 D.周期为的偶函数 [答案] A [解析] y=sin4x,T==. 又f(-x)=sin(-4x)=-sin4x=-f(x),它是奇函数. 2.若f(tanx)=sin2x,则f(-1)=( ) A.-2 B.-1 C.0 D.1 [答案] B [解析] f(-1)=f[tan(-+kπ)]=sin2(-+kπ)=sin(-+2kπ)=-1. 3.·等于( ) A.tanα B.tan2α C.1 D. [答案] B [解析] 原式====tan2α. 4.已知钝角α满足cosα=-,则sin等于( ) A. B. C. D. [答案] C [解析] ∵α为钝角,∴sin>0. ∴sin===. 5.若=-,则cosα+sinα的值为( ) A.- B.- C. D. [答案] C [解析] 法一:原式左边= = =-2cos=-(sinα+cosα)=-, ∴sinα+cosα=,故选C. 法二:原式= = =-(sinα+cosα)=-, ∴cosα+sinα=,故选C. 6.(2012·全国高考山东卷)若θ∈,sin2θ=,则sinθ=( ) A. B. C. D. [答案] D [解析] 由θ∈可得2θ∈,cos2θ=-=-,sinθ==,答案应选D. 另解:由θ∈及sin2θ=可得 sinθ+cosθ=====+, 而当θ∈时sinθ>cosθ, 结合选项即可得sinθ=,cosθ=.答案应选D. 二、填空题 7.已知tan=,则cosα=________. [答案] [解析] ∵tan=±, ∴tan2=. ∴=,解得cosα=. 8.函数f(x)=2cos2+sinx的最小正周期是________. [答案] 2π [解析] 化简得f(x)=1+sin(x+), ∴T==2π. 9.若sin=,则tan2x=________. [答案] 4 [解析] sin=-cos2x=sin2x-cos2x ===, 解得tan2x=4. 三、解答题 10.已知sinα=,sin(α+β)=,α、 β均为锐角,求cos的值. [解析] ∵0<α<,sinα=, ∴cosα==. 又∵0<α<,0<β<,∴0<α+β<π. 若0<α+β<, ∵>,即sinα>sin(α+β), ∴α+β<α不可能.∴<α+β<π. 又∵sin(α+β)=,∴cos(α+β)=-. ∴cosβ=cos[(α+β)-α] =cos(α+β)cosα+sin(α+β)sinα =-×+×=. 而0<β<,0<<, ∴cos==. 11.已知向量m=(cosθ,sinθ)和n=(-sinθ,cosθ),θ∈(π,2π),且|m+n|=,求cos(+)的值. [解析] m+n=(cosθ-sinθ+,cosθ+sinθ), ∵π<θ<2π,∴<+<. ∴cos(+)<0. 由已知|m+n|=,得 |m+n|= = = ==2 =2 =-2cos(+)=, ∴cos(+)=-. 12.(2013山东潍坊高一期末)已知cos(π-α)=, α∈(-π,0). (Ⅰ)求sinα. (Ⅱ)求cos2(-)+sin(3π+)·sin(π-)的值. [解析] (Ⅰ)∵cos(π-α)=-cosα=, ∴cosα=-, 又∵α∈(-π,0), ∴sinα=-=-. (Ⅱ)cos2(-)+sin(3π+)·sin(-) =[1+cos(-α)]+(-sin)·(-cos) =+sinα+sin·cos =+sinα+sinα =+sinα =+(-)=.查看更多