- 2021-06-19 发布 |
- 37.5 KB |
- 11页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2019高三数学(北师大版理科)一轮:单元质检卷十+算法初步、统计与统计案例
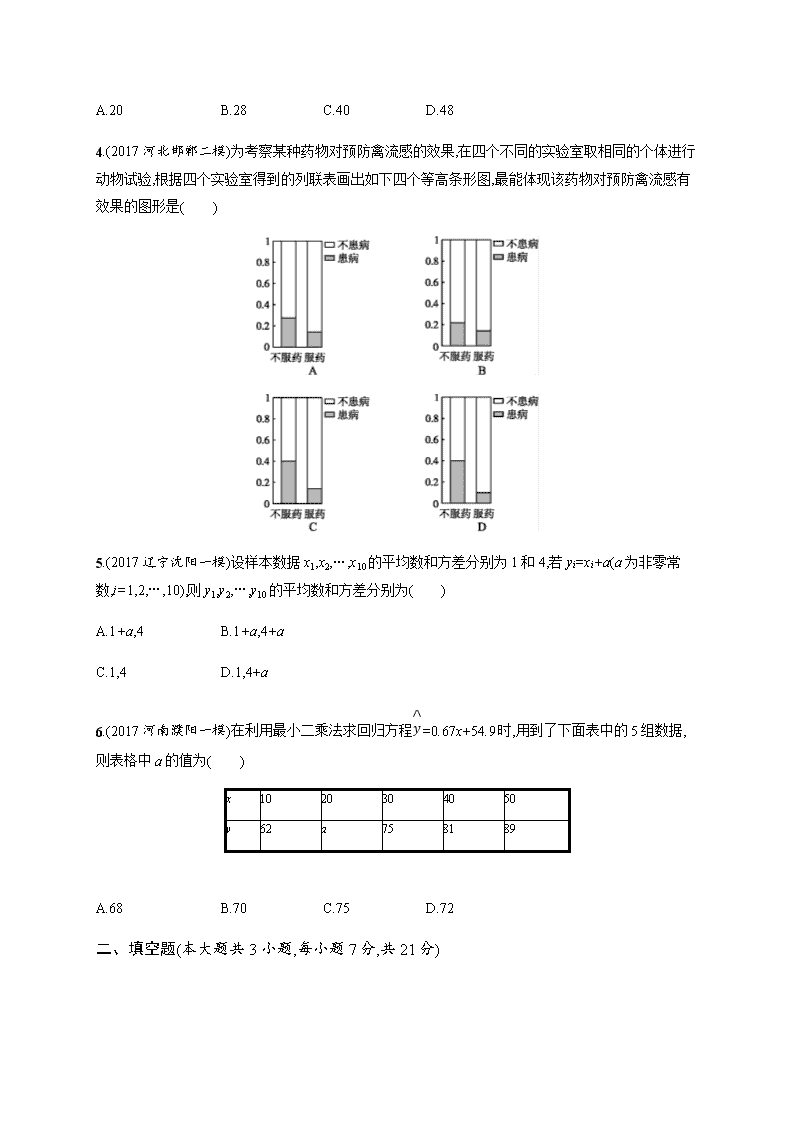
单元质检卷十 算法初步、统计与统计案例 (时间:45分钟 满分:100分) 一、选择题(本大题共6小题,每小题7分,共42分) 1.(2017江西鹰潭一模拟,理6)如图的算法框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”.执行该算法框图,若输入a,b,i的值分别为6,8,0,则输出a和i的值分别为( ) A.2,4 B.2,5 C.0,4 D.0,5 2.某大学对1 000名学生的自主招生水平测试成绩进行统计,得到样本频率分布直方图(如图),则这1 000名学生在该次自主招生水平测试中成绩不低于70分的学生人数是( ) A.300 B.400 C.500 D.600〚导学号21500650〛 3.(2017山东烟台一模,理4)用0,1,2,…,299给300名高三学生编号,并用系统抽样的方法从中抽取15名学生的数学成绩进行质量分析,若第一组抽取的学生的编号为8,则第三组抽取的学生的编号为( ) A.20 B.28 C.40 D.48 4.(2017河北邯郸二模)为考察某种药物对预防禽流感的效果,在四个不同的实验室取相同的个体进行动物试验,根据四个实验室得到的列联表画出如下四个等高条形图,最能体现该药物对预防禽流感有效果的图形是( ) 5.(2017辽宁沈阳一模)设样本数据x1,x2,…,x10的平均数和方差分别为1和4,若yi=xi+a(a为非零常数,i=1,2,…,10),则y1,y2,…,y10的平均数和方差分别为( ) A.1+a,4 B.1+a,4+a C.1,4 D.1,4+a 6.(2017河南濮阳一模)在利用最小二乘法求回归方程y^=0.67x+54.9时,用到了下面表中的5组数据,则表格中a的值为( ) x 10 20 30 40 50 y 62 a 75 81 89 A.68 B.70 C.75 D.72 二、填空题(本大题共3小题,每小题7分,共21分) 7.(2017河北衡水金卷一)在高三某次数学测试中,40名优秀学生的成绩如图所示.若将成绩由低到高编为1~40号,再用系统抽样的方法从中抽取8人,则其中成绩在区间[123,134]上的学生人数为 . 8.某高校进行自主招生,先从报名者中筛选出400人参加笔试,再按笔试成绩择优选出100人参加面试.现随机调查了24名笔试者的成绩,如下表所示: 分数段 [60,65) [65,70) [70,75) [75,80) [80,85) [85,90] 人数 2 3 4 9 5 1 据此估计允许参加面试的分数线大约是 分. 9.(2017北京西城区一模,理11)执行如图所示的算法框图,输出的S的值为 . 〚导学号21500651〛 三、解答题(本大题共3小题,共37分) 10.(12分)电视传媒公司为了解某地区电视观众对某类体育节目的收视情况,随机抽取了100名观众进行调查.下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图: 将日均收看该体育节目时间不低于40分的观众称为“体育迷”. (1)根据已知条件完成下面的2×2列联表,并据此资料你是否有95%的把握认为“体育迷”与性别有关? 非体育迷 体育迷 合计 男 女 10 55 合计 (2)将上述调查所得到的频率视为概率.现在从该地区大量电视观众中,采用随机抽样方法每次抽取1名观众,抽取3次,记被抽取的3名观众中的“体育迷”人数为X.若每次抽取的结果是相互独立的,求X的分布列,期望EX和方差DX. 附:χ2=n(ad-bc)2(a+b)(c+d)(a+c)(b+d). 11.(12分)(2017湖南衡阳三模,理17)全世界人们越来越关注环境保护问题,某监测站点于2016年8月某日起连续n天监测空气质量指数(AQI),数据统计如下: 区间 空气 质量指 数(μg/m3) [0,50) [50,100) [100,150) [150,200) [200,250] 空气质量等级 空气优 空气良 轻度污染 中度污染 重度污染 天 数 20 40 m 10 5 (1)根据所给统计表和频率分布直方图中的信息求出n,m的值,并完成频率分布直方图; (2)由频率分布直方图求该组数据的平均数与中位数; (3)在空气质量指数分别属于[50,100)和[150,200)的监测数据中,用分层抽样的方法抽取5天,再从中任意选取2天,求事件A“两天空气都为良”发生的概率. 12.(13分)(2017宁夏石嘴山三中三模,理18)某单位共有10名员工,他们某年的收入如下表: 员工编号 1 2 3 4 5 6 7 8 9 10 年薪(万元) 4 4.5 6 5 6.5 7.5 8 8.5 9 51 (1)求该单位员工当年年薪的平均值和中位数; (2)从该单位中任选2人,此2人中年薪收入高于7万的人数记为X,求X的分布列和期望; (3)已知员工年薪收入与工作年限成正相关关系,某员工工作第1年至第4年的年薪分别为4万元、5.5万元、6万元、8.5万元,预测该员工第5年的年薪为多少? 附:线性回归方程y=bx+a中的系数计算公式分别为: b=∑i=1n(xi-x)(yi-y)∑i=1n(xi-x)2,a=y-bx,其中x,y为样本均值. 参考答案 单元质检卷十 算法初步、 统计与统计案例 1.A 执行算法框图,可得a=6,b=8,i=0,i=1,不满足a>b,不满足a=b,b=8-6=2;i=2,满足a>b,a=6-2=4;i=3,满足a>b,a=4-2=2;i=4,不满足a>b,满足a=b,输出a的值为2,i的值为4,故选A. 2.D 依题意得,题中的1 000名学生在该次自主招生水平测试中成绩不低于70分的学生人数是1 000×(0.035+0.015+0.010)×10=600,故选D. 3.D ∵用系统抽样的方法从300名高三学生中抽取15个样本,∴组距是20. ∵第一组抽取的学生的编号为8, ∴第三组抽取的学生的编号为8+40=48.故选D. 4.D 根据四个列联表中的等高条形图知,图形D中不服药与服药时患禽流感的差异最大,它最能体现该药物对预防禽流感有效果.故选D. 5.A 由题意知yi=xi+a,则y=110(x1+x2+…+x10+10a)=110(x1+x2+…+x10)+a=x+a=1+a, 方差s2=110[(x1+a-x-a)2+(x2+a-x-a)2+…+(x10+a-x-a)2] =110[(x1-x)2+(x2-x)2+…+(x10-x)2]=4.故选A. 6.A 由题意可得x=15(10+20+30+40+50)=30,y=15(62+a+75+81+89)=15(a+307), 因为回归直线方程y=0.67x+54.9过样本点的中心,所以15(a+307)=0.67×30+54.9,解得a=68. 7.3 根据茎叶图,成绩在区间[123,134]上的学生有15人, 所以用系统抽样的方法从40人中抽取8人, 成绩在区间[123,134]上的学生人数为8×1540=3. 8.80 因为参加笔试的400人中择优选出100人参加面试,所以每个人被择优选出的概率P=100400=14.因为随机调查24名笔试者的成绩,所以估计能够参加面试的人数为24×14=6,观察题中表格可知,分数在[80,85)的有5人,分数在[85,90]的有1人,故面试的分数线大约为80分. 9.6 S=20,k=1, k=2,S=18; k=4,S=14; k=8,S=6. 此时满足k>5,输出S=6. 10.解 (1)由频率分布直方图可知,在抽取的100人中,“体育迷”有25人,从而2×2列联表如下: 非体育迷 体育迷 合计 男 30 15 45 女 45 10 55 合计 75 25 100 将2×2列联表中的数据代入公式计算,得 χ2=100×(30×10-45×15)275×25×45×55=10033≈3.030. 因为3.030<3.841,所以没有95%的把握认为“体育迷”与性别有关. (2)由频率分布直方图知抽到“体育迷”的频率为0.25,将频率视为概率,即从观众中抽取一名“体育迷”的概率为14. 由题意X~B3,14,从而X的分布列为 X 0 1 2 3 P 2764 2764 964 164 EX=np=3×14=34, DX=np(1-p)=3×14×34=916. 11.解 (1)0.004×50=20n,解得n=100.20+40+m+10+5=100,解得m=25, 40100×50=0.008,25100×50=0.005,10100×50=0.002,5100×50=0.001. 完成频率分布直方图如下图. (2)由频率分布直方图知该组数据的平均数为: x=25×0.004×50+75×0.008×50+125×0.005×50+175×0.002×50+225×0.001×50=95. ∵[0,50)的频率为0.004×50=0.2,[50,100)的频率为0.008×50=0.4, ∴该组数据的中位数为:50+0.5-0.20.4×50=87.5. (3)空气质量指数为[50,100)和[150,200)的监测天数中分别抽取4天和1天, 则基本事件总数为C52=10,事件A“两天空气都为良”有C42=6种, 故事件A“两天空气都为良”发生的概率P(A)=610=35. 12.解 (1)平均值为11万元,中位数为7万元. (2)年薪高于7万的有5人,低于或等于7万的有5人;X的取值为0,1,2. P(X=0)=C52C102=29,P(X=1)=C51C51C102=59,P(X=2)=C52C102=29, 所以X的分布列为 X 0 1 2 P 29 59 29 数学期望为EX=0×29+1×59+2×29=1. (3)设xi,yi(i=1,2,3,4)分别表示员工工作年限及相应年薪,则x=2.5,y=6, ∑i=14(xi-x)2=2.25+0.25+0.25+2.25=5, ∑i=14(xi-x)(yi-y)=(-1.5)×(-2)+(-0.5)×(-0.5)+0.5×0+1.5×2.5=7, b=∑i=14(xi-x)(yi-y)∑i=14(xi-x)2=75=1.4, a=y-bx=6-1.4×2.5=2.5, 得线性回归方程y=1.4x+2.5. 当x=5时,y=1.4×5+2.5=9.5(万元). 可预测该员工第5年的年薪收入为9.5万元.查看更多