新疆维吾尔自治区喀什第二中学2019-2020学年高一4月月考数学试题（含答案）

新疆维吾尔自治区喀什第二中学2019-2020学年高一4月月考数学试题（含答案）

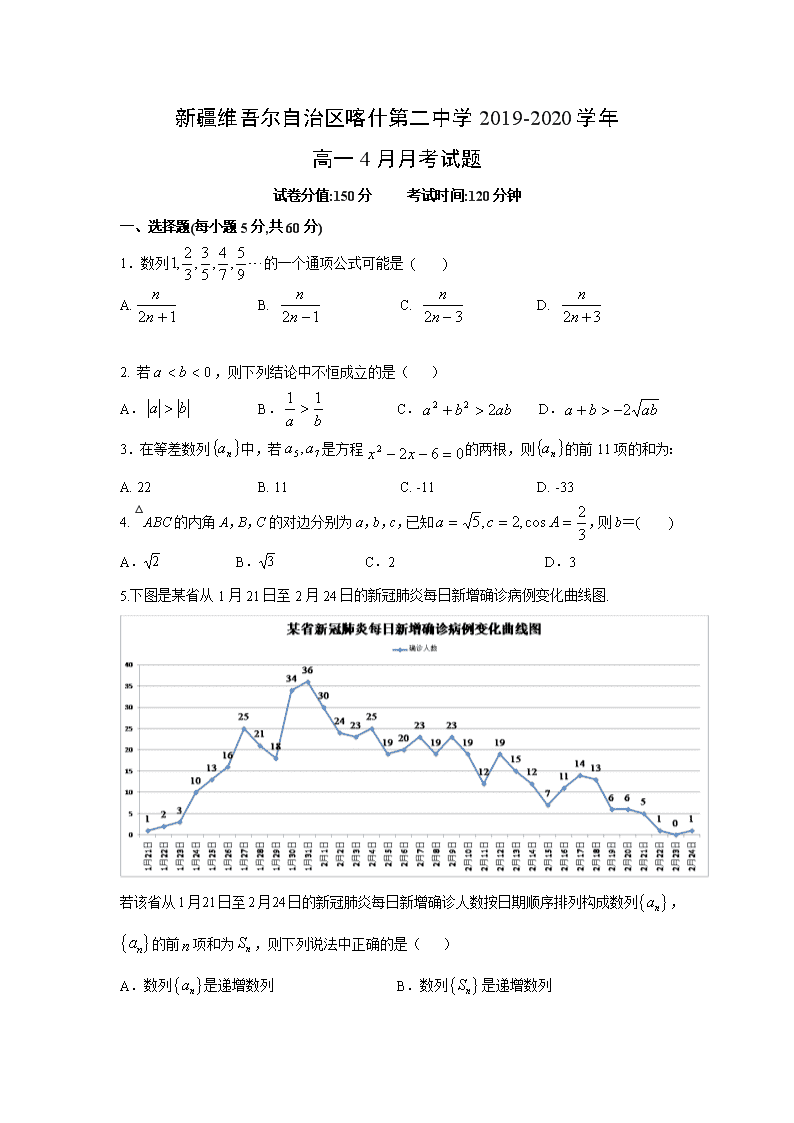
新疆维吾尔自治区喀什第二中学2019-2020学年 高一4月月考试题 试卷分值:150分 考试时间:120分钟 ‎ 一、选择题(每小题5分,共60分)‎ ‎1．数列的一个通项公式可能是 ( 　)‎ A. B. C. D. ‎ ‎2. 若，则下列结论中不恒成立的是（ ）‎ A． B． C． D．‎ ‎3．在等差数列中，若是方程的两根，则的前11项的和为：‎ A. 22 B. 11 C. -11 D. -33‎ ‎4. △ABC的内角A，B，C的对边分别为a，b，c，已知，则b＝(　　)‎ A． B． C．2 D．3‎ ‎5.下图是某省从1月21日至2月24日的新冠肺炎每日新增确诊病例变化曲线图.‎ 若该省从1月21日至2月24日的新冠肺炎每日新增确诊人数按日期顺序排列构成数列，的前项和为，则下列说法中正确的是（ ）‎ A．数列是递增数列 B．数列是递增数列 C．数列的最大项是 D．数列的最大项是 ‎6．设的内角A，B，C所对边分别为a，b，c若，则B=( )‎ A. B. C. 或 D. ‎ ‎7.下列函数中，最小值是4的函数是(　　)‎ A．y＝x＋ B．y＝sin x＋(0＜x＜π) ‎ C．y＝ex＋4e－x D．y＝log3x＋logx81‎ ‎8．已知实数，若，则的最小值是（ ）‎ A． B． C． 4 D．8‎ ‎9.设x，y满足约束条件，则z=x+y的最大值为（　　）‎ A. 3 B. 2 C. 1 D. 0‎ ‎10. 等差数列‎{an}‎的前n项和为，且，则　( 　)‎ A. -30 B. -15 C. 10 D. 25‎ ‎11．已知数列满足: ，设数列的前项和为，则（）‎ A．1007 B．1008 C．1009.5 D．1010 ‎ ‎12．在中，角A、B、C所对的边分别为a、b、c，且若，则的形状是(　　)‎ A.等腰三角形 B. 直角三角形 C. 等边三角形 D. 等腰直角三角形 二、填空题(每小题5分,共20分)‎ ‎13．不等式的解是___________ ‎ ‎14. 已知数列‎{an}‎的前n项和，则__________‎ ‎15．在中,角A，B，C的对边分别为a，b，c，若，则B=‎_________‎ ‎16. 在中，角A、B、C的对边分别为a，b，c，已知则下列结论正确的是_____________‎ ‎①一定是钝角三角形；    ②被唯一确定；‎ ‎③ ④若,则的面积为 三、解答题(17题10分,18-22题各12分,共70分)‎ ‎17．已知不等式x2-2x-3＜0的解集为A，不等式x2+x-6＜0的解集为B．‎ ‎（1）求A∩B；‎ ‎（2）若不等式x2+ax+b＜0的解集为A∩B，求a，b的值．‎ ‎18. 已知数列是公比为2的等比数列，且成等差数列．‎ ‎(1)求数列的通项公式；‎ ‎(2)记，求数列的前n项和Tn．‎ ‎19. 已知公差不为零的等差数列满足：，且是与的等比中项．‎ ‎(1)求数列的通项公式；‎ ‎(2)设数列满足，求数列的前n项和．‎ ‎20.已知a，b，c分别是内角A，B，C的对边，且满足．‎ ‎(1)求角A的大小；‎ ‎(2)若，求的面积．‎ ‎21.已知关于x的一元二次不等式的解集为R.‎ (1) 求实数m的取值范围； ‎ (2) 求函数的最小值；‎ (3) 解关于x的一元二次不等式.‎ ‎22．△ABC的内角A，B，C的对边分别为a，b，c，已知a＝bcos C＋csinB．‎ ‎(1)求B；‎ ‎(2)若b＝2，求△ABC面积的最大值。‎ 参考答案 一、选择题(每小题5分,共60分)‎ ‎1-6 BDBDCA，7-12 CDABDC　‎ 二、填空题 ‎13． 14. 15． 16. ①③‎ 三、解答题 ‎17．解：（1）∵x2-2x-3＜0，∴（x-3）（x+1）＜0，解得：-1＜x＜3，∴A={x|-1＜x＜3}，‎ ‎∵x2+x-6＜0，∴（x+3）（x-2）＜0，解得：-3＜x＜2，∴B={x|-3＜x＜2}， ‎ ‎∴A∩B={x|-1＜x＜2}；‎ ‎（2）由（1）得：-1，2为方程x2+ax+b=0的两根，∴，∴．‎ ‎18. 解：（I）由题意可得，即，解得：, ∴数列的通项公式为； （II）​， ​ ​ =．‎ ‎19.解：（1）设等差数列{an}的公差为d， ∵a3+a8=20，且a5是a2与a14的等比中项， ∴，解得a1=1，d=2， ∴an=1+2（n-1）=2n-1． （2）bn==（）， ∴Sn=b1+b2+b3+…+bn =（1-+-+…+） ​ =（1-） ​ =．‎ ‎20.解：（1）∵（b-c）2=a2-bc，可得：b2+c2-a2=bc， ∴由余弦定理可得：cosA===， 又∵A∈（0，π），∴A=； （2）由sinC=2sinB及正弦定理可得c=2b，‎ ‎∵a=3，A=，∴由余弦定理可得a2=b2+c2-2bccosA=b2+c2-bc=3b2，‎ ‎∴解得：b=，c=2， ∴S△ABC=bcsinA​==.‎ ‎21..答案：（1）‎ ‎（2）当时，的最小值为 ‎（3）‎ ‎22．解：(1)由已知及正弦定理得，‎ sin A＝sin Bcos C＋sin CsinB ①‎ 又A＝π－(B＋C)，‎ 故sin A＝sin(B＋C)＝sin Bcos C＋cos Bsin C．②‎ 由①②和C∈(0，π)得sin B＝cosB．又B∈(0，π)，所以B＝．‎ ‎(2)△ABC的面积S＝acsin B＝ac．‎ 由已知及余弦定理得4＝a2＋c2－2accos．‎ 又a2＋c2≥2ac，故ac≤＝4＋2，当且仅当a＝c时等号成立．‎ 因此△ABC面积的最大值为(4＋2)＝＋1．‎