- 2021-06-19 发布 |
- 37.5 KB |
- 8页


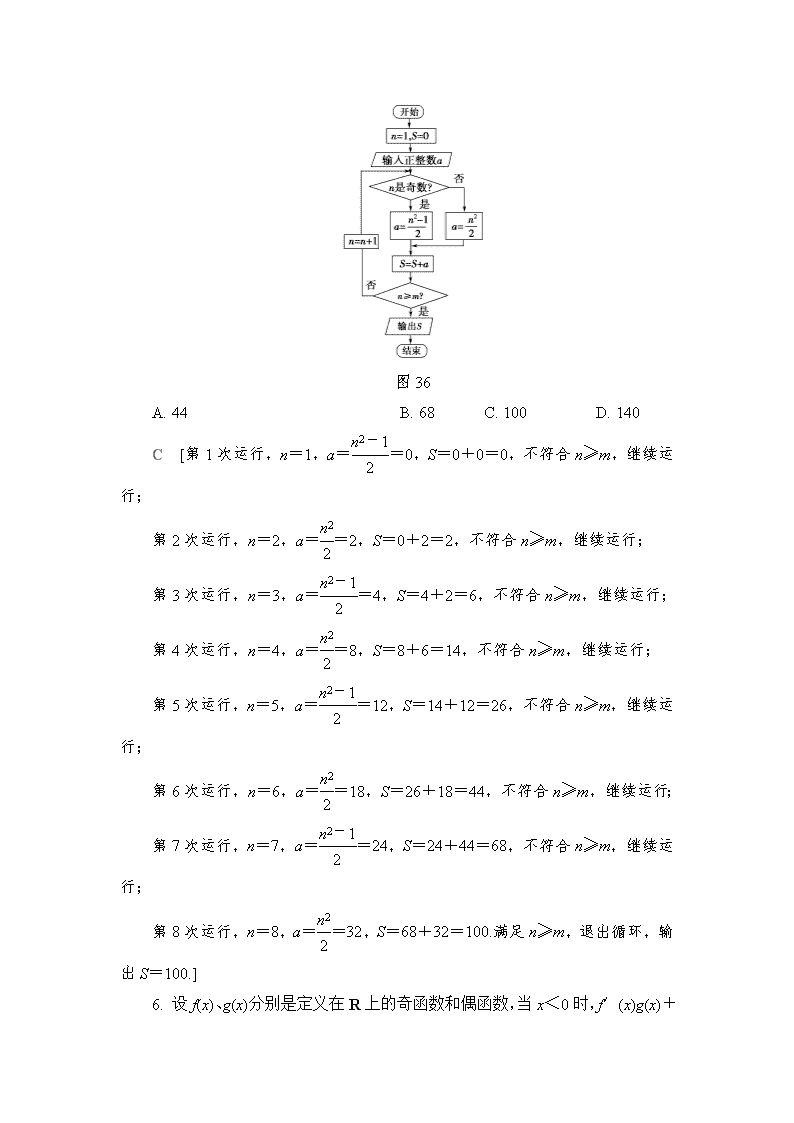
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2019届二轮复习小题分层练6 中档小题保分练(2)作业(全国通用)
小题分层练(六) 中档小题保分练(2) (建议用时:40分钟) 一、选择题 1.设等差数列{an}的前n项和为Sn,若S9=54,则2a6+a3=( ) A. 9 B. 15 C. 18 D. 36 C [S9=(a1+a9)=×2a5=9a5=54,∴a5=6. ∵2a6+a3=2(a1+5d)+a1+2d=3(a1+4d)=3a5=18,故选C.] 2.(2018·贵州二模)已知函数f(x)=是R上的偶函数,则g(3)=( ) A. 5 B. -5 C. 7 D. -7 B [∵函数f(x)=是R上的偶函数, ∴g(3)=f(-3)=-6+1=-5.] (教师备选) 已知函数f(x)=ax3+x2+x+1(a∈R),下列选项中不可能是函数f(x)图象的是( ) A B C D D [∵f(x)=ax3+x2+x+1(a∈R), ∴f′(x)=ax2+x+1. 当a=0时,f′(x)=x+1,易得f(x)在(-∞,-1)上为减函数,在(-1,+∞)上为增函数,故A正确; 当a≥时,Δ≤0,f′(x)≥0,f(x)为增函数,故B可能; 当a<0时,Δ>0,f′(x)有两个不相等且互为异号的实数根,f(x)先递减再递增然后再递减,故C正确; 当0<a<时,Δ>0,f′(x)有两个不相等的负实数根,f(x )先递增再递减然后再递增,故D错误. 故选D.] 3.已知抛物线C:y2=4x的焦点为F,点A(0,-).若线段FA与抛物线C相交于点M,则|MF|=( ) A. B. C. D. A [线段AF:y=x-(0≤x≤1).联立方程组解得M,所以|MF|=+1=,选A.] 4.将函数f(x)=cos 2x-sin 2x的图象向右平移θ个单位长度后得到的图象关于直线x=对称,则θ的最小正值为( ) A. B. C. D. C [将函数f(x)=cos 2x-sin 2x=2cos的图象向右平移θ个单位长度后,可得y=2cos2x-2θ+的图象.再根据得到的图象关于直线x=对称,可得-2θ+=kπ,k∈Z,即θ=-+,k∈Z,则θ的最小正值为,故选C.] 5.习总书记在十九大报告中指出:坚定文化自信,推动社会主义文化繁荣兴盛.“大衍数列”:0,2,4,8,12来源于《乾坤谱》中对《易传》“大衍之数五十”的推论,主要用于解释中国传统文化中的太极衍生过程中曾经经历过的两仪数量总和.如图36是求大衍数列前n项和的程序框图.执行该程序框图,输入m=8,则输出的S=( ) 图36 A. 44 B. 68 C. 100 D. 140 C [第1次运行,n=1,a==0,S=0+0=0,不符合n≥m,继续运行; 第2次运行,n=2,a==2,S=0+2=2,不符合n≥m,继续运行; 第3次运行,n=3,a==4,S=4+2=6,不符合n≥m,继续运行; 第4次运行,n=4,a==8,S=8+6=14,不符合n≥m,继续运行; 第5次运行,n=5,a==12,S=14+12=26,不符合n≥m,继续运行; 第6次运行,n=6,a==18,S=26+18=44,不符合n≥m,继续运行; 第7次运行,n=7,a==24,S=24+44=68,不符合n≥m,继续运行; 第8次运行,n=8,a==32,S=68+32=100.满足n≥m,退出循环,输出S=100.] 6. 设f(x)、g(x)分别是定义在R上的奇函数和偶函数,当x<0时,f′(x)g(x)+f(x)g′(x)>0.且g(3)=0.则不等式f(x)g(x)<0的解集是( ) A.(-∞,-3)∪(0,3) B.(-3,0)∪(0,3) C.(-∞,-3)∪(3,+∞) D.(-3,0)∪(3,+∞) A [因f′(x)g(x)+f(x)g′(x)>0,即[f(x)g(x)]′>0, 故f(x)g(x)在(-∞,0)上递增, 又∵f(x),g(x)分别是定义R上的奇函数和偶函数, ∴f(x)g(x)为奇函数,关于原点对称,所以f(x)g(x)在(0,+∞)上也是增函数. ∵f(3)g(3)=0,∴f(-3)g(-3)=0, 所以f(x)g(x)<0的解集为:x<-3或0<x<3.] (教师备选) 设x,y满足不等式若M=3x+y,N=x-,则M-N的最小值为( ) A. B.- C.1 D.-1 A [作出不等式组所表示的平面区域,如图中阴影部分所示,易求得A(-1,2),B(3,2),当直线3x+y-M=0经过点A(-1,2)时,目标函数M=3x+y取得最小值-1.又由平面区域知-1≤x≤3,所以函数N=x-在x=-1处取得最大值-,由此可得M-N的最小值为-1-=.] 7.(2018·江门一模)某几何体的三视图如图37所示,则该几何体的体积V=( ) 图37 A. B. C.3 D. B [由三视图可得,该几何体为直三棱柱截去一个三棱锥后所得的部分, 其中直三棱柱的底面是直角边为2的等腰直角三角形,高为2; 三棱锥的底面与棱柱的底面相同,高为1. 故几何体的体积为V=V柱-V锥=×22×2-××1=.选B.] 8.(2018·齐齐哈尔三模)如图38,四边形ABCD为正方形, G为线段BC的中点,四边形AEFG与四边形DGHI也为正方形,连接EB,CI,则向多边形AEFGHID中投掷一点,该点落在阴影部分内的概率为( ) 图38 A. B. C. D. A [设正方形ABCD的边长为1,S总=3,S阴影=2×××=1,所以概率为P=,故选A. ] (教师备选) (2018·陕西咸阳高三二模)已知甲、乙、丙三人中,一人是军人,一人是工人,一人是农民.若乙的年龄比农民的年龄大;丙的年龄和工人的年龄不同;工人的年龄比甲的年龄小,则下列判断正确的是( ) A. 甲是军人,乙是工人,丙是农民 B. 甲是农民,乙是军人,丙是工人 C. 甲是农民,乙是工人,丙是军人 D. 甲是工人,乙是农民,丙是军人 A [丙的年龄和工人的年龄不同,工人的年龄比甲的年龄小,则甲丙均不是工人,故乙是工人,乙的年龄比农民的年龄大,即工人的年龄比农民的年龄大,而工人的年龄比甲的年龄小,故甲不是农民,则丙是农民;最后可确定甲是军人.] 9.(2018·焦作三模)在三棱锥PABC中,AB=BC=,∠ABC=∠BCP=∠PAB=90°,cos∠CPA=,则三棱锥PABC外接球的表面积为( ) A.5π B.13π C.6π D.14π A [如图所示,作PE⊥平面ABC于E点,连接EA,EC, 因为BC⊥CP,PA⊥AB,易得EC⊥CB,EA⊥AB, 四边形EABC为矩形,PA2=1+PE2,PC2=3+PE2, 在△PAC中,由余弦定理PA2+PC2-2PA·PCcos∠CPA=4, 代入整理得PE=1,设三棱锥PABC外接球的半径为R, 由PE=1得2R=,即R=,所以球的表面积为S=4πR2=5π,故选A.] 二、填空题 10.(2018·包头一模)已知f(x)为奇函数,当x≤0时,f(x)=-x2-3x,则曲线y=f(x)在点(1,-2)处的切线方程为________. x+y+1=0 [由题意,当x>0时,则-x<0, 因为函数f(x)为奇函数,所以f(x)=-f(-x)=-[-(-x)2-3(-x)]=x2-3x, 所以当x>0时,f′(x)=2x-3,所以f′(1)=2×1-3=-1, 即切线的斜率为k=-1,所以在点(1,-2)的切线方程为y-(-2)=-1×(x-1),即x+y+1=0.] 11.若直线l:+=1与x轴、y轴分别相交于A,B两点,O为坐标原点,则△OAB的内切圆的方程为________. (x-1)2+(y-1)2=1 [由题意,设圆心为(a,a),则有=a,解得a=1或a=6(舍去),所以所求圆的方程为(x-1)2+(y-1)2=1.] (教师备选) 1.(2018·衡阳二模)在△ABC中,内角A,B,C所对的边分别是a,b,c,若=2sin C,则∠C的大小为________. [因为=2sin C,所以由正弦定理得=2sin C. ∴=2sin C,∴2abcos C=2absin C,∴tan C=1,∵C∈(0,π),∴C=.] 2.已知x,y满足约束条件其中k>0,若使得z=取得最小值的解(x,y)有无穷多个,则k的值为________. 2 [作出可行域如图:可得当z= 取得最小值的解有无穷多个时,满足点(-3,-2)在直线x-ky-1=0上可知-3+2k-1=0 解得k=2.]查看更多