- 2021-06-19 发布 |
- 37.5 KB |
- 28页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2014年江苏省高考数学试卷
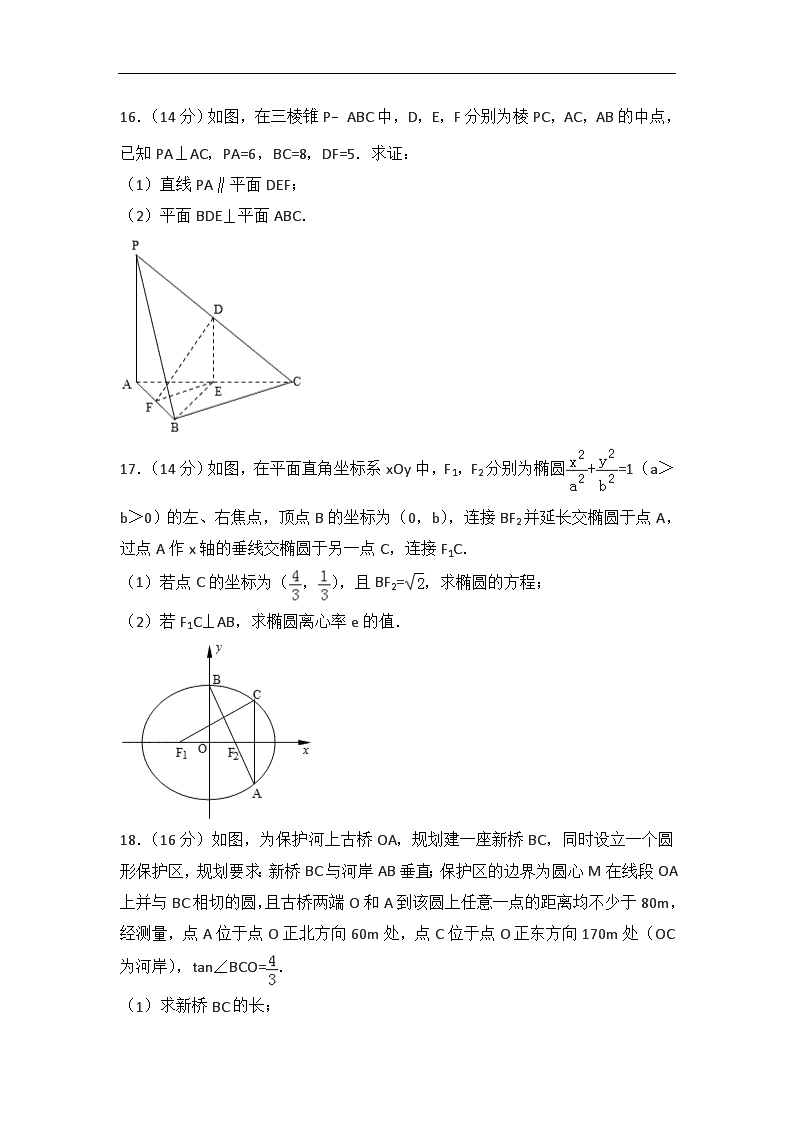
2014年江苏省高考数学试卷 一、填空题(本大题共14小题,每小题5分,共计70分) 1.(5分)已知集合A={﹣2,﹣1,3,4},B={﹣1,2,3},则A∩B= . 2.(5分)已知复数z=(5+2i)2(i为虚数单位),则z的实部为 . 3.(5分)如图是一个算法流程图,则输出的n的值是 . 4.(5分)从1,2,3,6这4个数中一次随机抽取2个数,则所取2个数的乘积为6的概率是 . 5.(5分)已知函数y=cosx与y=sin(2x+φ)(0≤φ<π),它们的图象有一个横坐标为的交点,则φ的值是 . 6.(5分)为了了解一片经济林的生长情况,随机抽测了其中60株树木的底部周长(单位:cm),所得数据均在区间[80,130]上,其频率分布直方图如图所示,则在抽测的60株树木中,有 株树木的底部周长小于100cm. 7.(5分)在各项均为正数的等比数列{an}中,若a2=1,a8=a6+2a4,则a6 的值是 . 8.(5分)设甲、乙两个圆柱的底面积分别为S1,S2,体积分别为V1,V2,若它们的侧面积相等,且=,则的值是 . 9.(5分)在平面直角坐标系xOy中,直线x+2y﹣3=0被圆(x﹣2)2+(y+1)2=4截得的弦长为 . 10.(5分)已知函数f(x)=x2+mx﹣1,若对于任意x∈[m,m+1],都有f(x)<0成立,则实数m的取值范围是 . 11.(5分)在平面直角坐标系xOy中,若曲线y=ax2+(a,b为常数)过点P(2,﹣5),且该曲线在点P处的切线与直线7x+2y+3=0平行,则a+b的值是 . 12.(5分)如图,在平行四边形ABCD中,已知AB=8,AD=5,=3,•=2,则•的值是 . 13.(5分)已知f(x)是定义在R上且周期为3的函数,当x∈[0,3)时,f(x)=|x2﹣2x+|,若函数y=f(x)﹣a在区间[﹣3,4]上有10个零点(互不相同),则实数a的取值范围是 . 14.(5分)若△ABC的内角满足sinA+sinB=2sinC,则cosC的最小值是 . 二、解答题(本大题共6小题,共计90分) 15.(14分)已知α∈(,π),sinα=. (1)求sin(+α)的值; (2)求cos(﹣2α)的值. 16.(14分)如图,在三棱锥P﹣ABC中,D,E,F分别为棱PC,AC,AB的中点,已知PA⊥AC,PA=6,BC=8,DF=5.求证: (1)直线PA∥平面DEF; (2)平面BDE⊥平面ABC. 17.(14分)如图,在平面直角坐标系xOy中,F1,F2分别为椭圆+=1(a>b>0)的左、右焦点,顶点B的坐标为(0,b),连接BF2并延长交椭圆于点A,过点A作x轴的垂线交椭圆于另一点C,连接F1C. (1)若点C的坐标为(,),且BF2=,求椭圆的方程; (2)若F1C⊥AB,求椭圆离心率e的值. 18.(16分)如图,为保护河上古桥OA,规划建一座新桥BC,同时设立一个圆形保护区,规划要求:新桥BC与河岸AB垂直;保护区的边界为圆心M在线段OA上并与BC相切的圆,且古桥两端O和A到该圆上任意一点的距离均不少于80m,经测量,点A位于点O正北方向60m处,点C位于点O正东方向170m处(OC为河岸),tan∠BCO=. (1)求新桥BC的长; (2)当OM多长时,圆形保护区的面积最大? 19.(16分)已知函数f(x)=ex+e﹣x,其中e是自然对数的底数. (1)证明:f(x)是R上的偶函数; (2)若关于x的不等式mf(x)≤e﹣x+m﹣1在(0,+∞)上恒成立,求实数m的取值范围; (3)已知正数a满足:存在x0∈[1,+∞),使得f(x0)<a(﹣x03+3x0)成立,试比较ea﹣1与ae﹣1的大小,并证明你的结论. 20.(16分)设数列{an}的前n项和为Sn,若对任意的正整数n,总存在正整数m,使得Sn=am,则称{an}是“H数列”. (1)若数列{an}的前n项和为Sn=2n(n∈N*),证明:{an}是“H数列”; (2)设{an}是等差数列,其首项a1=1,公差d<0,若{an}是“H数列”,求d的值; (3)证明:对任意的等差数列{an},总存在两个“H数列”{bn}和{cn},使得an=bn+cn(n∈N*)成立. 三、附加题(本大题包括选做题和必做题两部分)(一)选择题(本题包括21、22、23、24四小题,请选定其中两个小题作答,若多做,则按作答的前两个小题评分)【选修4-1:几何证明选讲】 21.(10分)如图,AB是圆O的直径,C,D是圆O上位于AB异侧的两点,证明:∠OCB=∠D. 【选修4-2:矩阵与变换】 22.(10分)已知矩阵A=,B=,向量=,x,y为实数,若A=B,求x+y的值. 【选修4-3:极坐标及参数方程】 23.在平面直角坐标系xOy中,已知直线l的参数方程为(t为参数),直线l与抛物线y2=4x相交于A,B两点,求线段AB的长. 【选修4-4:不等式选讲】 24.已知x>0,y>0,证明(1+x+y2)(1+x2+y)≥9xy. (二)必做题(本部分包括25、26两题,每题10分,共计20分) 25.(10分)盒中共有9个球,其中有4个红球,3个黄球和2个绿球,这些球除颜色外完全相同. (1)从盒中一次随机取出2个球,求取出的2个球颜色相同的概率P; (2)从盒中一次随机取出4个球,其中红球、黄球、绿球的个数分别记为x1,x2,x3,随机变量X表示x1,x2,x3中的最大数,求X的概率分布和数学期望E(X). 26.(10分)已知函数f0(x)=(x>0),设fn(x)为fn﹣1(x)的导数,n∈N*. (1)求2f1()+f2()的值; (2)证明:对任意n∈N*,等式|nfn﹣1()+fn()|=都成立. 2014年江苏省高考数学试卷 参考答案与试题解析 一、填空题(本大题共14小题,每小题5分,共计70分) 1.(5分)(2014•江苏)已知集合A={﹣2,﹣1,3,4},B={﹣1,2,3},则A∩B= {﹣1,3} . 【分析】根据集合的基本运算即可得到结论. 【解答】解:∵A={﹣2,﹣1,3,4},B={﹣1,2,3}, ∴A∩B={﹣1,3}, 故答案为:{﹣1,3} 2.(5分)(2014•江苏)已知复数z=(5+2i)2(i为虚数单位),则z的实部为 21 . 【分析】根据复数的有关概念,即可得到结论. 【解答】解:z=(5+2i)2=25+20i+4i2=25﹣4+20i=21+20i, 故z的实部为21, 故答案为:21 3.(5分)(2014•江苏)如图是一个算法流程图,则输出的n的值是 5 . 【分析】算法的功能是求满足2n>20的最小的正整数n的值,代入正整数n验证可得答案. 【解答】解:由程序框图知:算法的功能是求满足2n>20的最小的正整数n的值, ∵24=16<20,25=32>20, ∴输出n=5. 故答案为:5. 4.(5分)(2014•江苏)从1,2,3,6这4个数中一次随机抽取2个数,则所取2个数的乘积为6的概率是 . 【分析】首先列举并求出“从1,2,3,6这4个数中一次随机抽取2个数”的基本事件的个数再从中找到满足“所取2个数的乘积为6”的事件的个数,利用概率公式计算即可. 【解答】解:从1,2,3,6这4个数中一次随机抽取2个数的所有基本事件有(1,2),(1,3),(1,6),(2,3),(2,6),(3,6)共6个, 所取2个数的乘积为6的基本事件有(1,6),(2,3)共2个, 故所求概率P=. 故答案为:. 5.(5分)(2014•江苏)已知函数y=cosx与y=sin(2x+φ)(0≤φ< π),它们的图象有一个横坐标为的交点,则φ的值是 . 【分析】由于函数y=cosx与y=sin(2x+φ),它们的图象有一个横坐标为的交点,可得=.根据φ的范围和正弦函数的单调性即可得出. 【解答】解:∵函数y=cosx与y=sin(2x+φ),它们的图象有一个横坐标为的交点, ∴=. ∵0≤φ<π,∴, ∴+φ=, 解得φ=. 故答案为:. 6.(5分)(2014•江苏)为了了解一片经济林的生长情况,随机抽测了其中60株树木的底部周长(单位:cm),所得数据均在区间[80,130]上,其频率分布直方图如图所示,则在抽测的60株树木中,有 24 株树木的底部周长小于100cm. 【分析】根据频率=小矩形的面积=小矩形的高×组距底部求出周长小于100cm的频率,再根据频数=样本容量×频率求出底部周长小于100cm的频数. 【解答】解:由频率分布直方图知:底部周长小于100cm的频率为(0.015+0.025)×10=0.4, ∴底部周长小于100cm的频数为60×0.4=24(株). 故答案为:24. 7.(5分)(2014•江苏)在各项均为正数的等比数列{an}中,若a2=1,a8=a6+2a4,则a6的值是 4 . 【分析】利用等比数列的通项公式即可得出. 【解答】解:设等比数列{an}的公比为q>0,a1>0. ∵a8=a6+2a4, ∴, 化为q4﹣q2﹣2=0,解得q2=2. ∴a6===1×22=4. 故答案为:4. 8.(5分)(2014•江苏)设甲、乙两个圆柱的底面积分别为S1,S2,体积分别为V1,V2,若它们的侧面积相等,且=,则的值是 . 【分析】设出两个圆柱的底面半径与高,通过侧面积相等,推出高的比,然后求解体积的比. 【解答】解:设两个圆柱的底面半径分别为R,r;高分别为H,h; ∵=, ∴,它们的侧面积相等, ∴, ∴===. 故答案为:. 9.(5分)(2014•江苏)在平面直角坐标系xOy中,直线x+2y﹣3=0被圆(x﹣2)2+(y+1)2=4截得的弦长为 . 【分析】求出已知圆的圆心为C(2,﹣1),半径r=2.利用点到直线的距离公式,算出点C到直线直线l的距离d,由垂径定理加以计算,可得直线x+2y﹣3=0被圆截得的弦长. 【解答】解:圆(x﹣2)2+(y+1)2=4的圆心为C(2,﹣1),半径r=2, ∵点C到直线直线x+2y﹣3=0的距离d==, ∴根据垂径定理,得直线x+2y﹣3=0被圆(x﹣2)2+(y+1)2=4截得的弦长为2=2= 故答案为:. 10.(5分)(2014•江苏)已知函数f(x)=x2+mx﹣1,若对于任意x∈[m,m+1],都有f(x)<0成立,则实数m的取值范围是 (﹣,0) . 【分析】由条件利用二次函数的性质可得 ,由此求得m的范围. 【解答】解:∵二次函数f(x)=x2+mx﹣1的图象开口向上, 对于任意x∈[m,m+1],都有f(x)<0成立,∴, 即 ,解得﹣<m<0, 故答案为:(﹣,0). 11.(5分)(2014•江苏)在平面直角坐标系xOy中,若曲线y=ax2+(a,b为常数)过点P(2,﹣5),且该曲线在点P处的切线与直线7x+2y+3=0平行,则a+b的值是 ﹣3 . 【分析】由曲线y=ax2+(a,b为常数)过点P(2,﹣5),且该曲线在点P处的切线与直线7x+2y+3=0平行,可得y|x=2=﹣5,且y′|x=2=,解方程可得答案. 【解答】解:∵直线7x+2y+3=0的斜率k=, 曲线y=ax2+(a,b为常数)过点P(2,﹣5),且该曲线在点P处的切线与直线7x+2y+3=0平行, ∴y′=2ax﹣, ∴, 解得:, 故a+b=﹣3, 故答案为:﹣3 12.(5分)(2014•江苏)如图,在平行四边形ABCD中,已知AB=8,AD=5,=3,•=2,则•的值是 22 . 【分析】由=3,可得=+,=﹣,进而由AB=8,AD=5,=3,•=2,构造方程,进而可得答案. 【解答】解:∵=3, ∴=+,=﹣, 又∵AB=8,AD=5, ∴•=(+)•(﹣)=||2﹣•﹣||2=25﹣•﹣12=2, 故•=22, 故答案为:22. 13.(5分)(2014•江苏)已知f(x)是定义在R上且周期为3的函数,当x∈[0,3)时,f(x)=|x2﹣2x+|,若函数y=f(x)﹣a在区间[﹣3,4]上有10个零点(互不相同),则实数a的取值范围是 (0,) . 【分析】在同一坐标系中画出函数的图象与直线y=a的图象,利用数形结合判断a的范围即可. 【解答】解:f(x)是定义在R上且周期为3的函数,当x∈[0,3)时,f(x)=|x2﹣2x+|,若函数y=f(x)﹣a在区间[﹣3,4]上有10个零点(互不相同),在同一坐标系中画出函数f(x)与y=a的图象如图:由图象可知. 故答案为:(0,). 14.(5分)(2014•江苏)若△ABC的内角满足sinA+sinB=2sinC,则cosC的最小值是 . 【分析】根据正弦定理和余弦定理,利用基本不等式即可得到结论. 【解答】解:由正弦定理得a+b=2c,得c=(a+b), 由余弦定理得cosC=== =≥=, 当且仅当时,取等号, 故≤cosC<1,故cosC的最小值是. 故答案为:. 二、解答题(本大题共6小题,共计90分) 15.(14分)(2014•江苏)已知α∈(,π),sinα=. (1)求sin(+α)的值; (2)求cos(﹣2α)的值. 【分析】(1)通过已知条件求出cosα,然后利用两角和的正弦函数求sin(+α)的值; (2)求出cos2α,然后利用两角差的余弦函数求cos(﹣2α)的值. 【解答】解:α∈(,π),sinα=.∴cosα=﹣= (1)sin(+α)=sincosα+cossinα==﹣; ∴sin(+α)的值为:﹣. (2)∵α∈(,π),sinα=.∴cos2α=1﹣2sin2α=,sin2α=2sinαcosα=﹣ ∴cos(﹣2α)=coscos2α+sinsin2α==﹣ . cos(﹣2α)的值为:﹣. 16.(14分)(2014•江苏)如图,在三棱锥P﹣ABC中,D,E,F分别为棱PC,AC,AB的中点,已知PA⊥AC,PA=6,BC=8,DF=5.求证: (1)直线PA∥平面DEF; (2)平面BDE⊥平面ABC. 【分析】(1)由D、E为PC、AC的中点,得出DE∥PA,从而得出PA∥平面DEF; (2)要证平面BDE⊥平面ABC,只需证DE⊥平面ABC,即证DE⊥EF,且DE⊥AC即可. 【解答】证明:(1)∵D、E为PC、AC的中点,∴DE∥PA, 又∵PA⊄平面DEF,DE⊂平面DEF, ∴PA∥平面DEF; (2)∵D、E为PC、AC的中点,∴DE=PA=3; 又∵E、F为AC、AB的中点,∴EF=BC=4; ∴DE2+EF2=DF2, ∴∠DEF=90°, ∴DE⊥EF; ∵DE∥PA,PA⊥AC,∴DE⊥AC; ∵AC∩EF=E,∴DE⊥平面ABC; ∵DE⊂平面BDE,∴平面BDE⊥平面ABC. 17.(14分)(2014•江苏)如图,在平面直角坐标系xOy中,F1,F2分别为椭圆+=1(a>b>0)的左、右焦点,顶点B的坐标为(0,b),连接BF2并延长交椭圆于点A,过点A作x轴的垂线交椭圆于另一点C,连接F1C. (1)若点C的坐标为(,),且BF2=,求椭圆的方程; (2)若F1C⊥AB,求椭圆离心率e的值. 【分析】(1)根据椭圆的定义,建立方程关系即可求出a,b的值. (2)求出C的坐标,利用F1C⊥AB建立斜率之间的关系,解方程即可求出e的值. 【解答】解:(1)∵C的坐标为(,), ∴,即, ∵, ∴a2=()2=2,即b2=1, 则椭圆的方程为+y2=1. (2)设F1(﹣c,0),F2(c,0), ∵B(0,b), ∴直线BF2:y=﹣x+b,代入椭圆方程+=1(a>b>0)得()x2﹣ =0, 解得x=0,或x=, ∵A(,),且A,C关于x轴对称, ∴C(,﹣), 则=﹣=, ∵F1C⊥AB, ∴×()=﹣1, 由b2=a2﹣c2得, 即e=. 18.(16分)(2014•江苏)如图,为保护河上古桥OA,规划建一座新桥BC,同时设立一个圆形保护区,规划要求:新桥BC与河岸AB垂直;保护区的边界为圆心M在线段OA上并与BC相切的圆,且古桥两端O和A到该圆上任意一点的距离均不少于80m,经测量,点A位于点O正北方向60m处,点C位于点O正东方向170m处(OC为河岸),tan∠BCO=. (1)求新桥BC的长; (2)当OM多长时,圆形保护区的面积最大? 【分析】(1)在四边形AOCB中,过B作BE⊥OC于E,过A作AF⊥BE于F,设出AF,然后通过解直角三角形列式求解BE,进一步得到CE,然后由勾股定理得答案; (2)设BC与⊙M切于Q,延长QM、CO交于P,设OM=xm,把PC、PQ用含有x的代数式表示,再结合古桥两端O和A到该圆上任意一点的距离均不少于80m列式求得x的范围,得到x取最小值时圆的半径最大,即圆形保护区的面积最大. 【解答】解:(1)如图, 过B作BE⊥OC于E,过A作AF⊥BE于F, ∵∠ABC=90°,∠BEC=90°, ∴∠ABF=∠BCE, ∴. 设AF=4x(m),则BF=3x(m). ∵∠AOE=∠AFE=∠OEF=90°, ∴OE=AF=4x(m),EF=AO=60(m), ∴BE=(3x+60)m. ∵, ∴CE=(m). ∴(m). ∴, 解得:x=20. ∴BE=120m,CE=90m, 则BC=150m; (2)如图, 设BC与⊙M切于Q,延长QM、CO交于P, ∵∠POM=∠PQC=90°, ∴∠PMO=∠BCO. 设OM=xm,则OP=m,PM=m. ∴PC=m,PQ=m. 设⊙M半径为R, ∴R=MQ=m=m. ∵A、O到⊙M上任一点距离不少于80m, 则R﹣AM≥80,R﹣OM≥80, ∴136﹣﹣(60﹣x)≥80,136﹣﹣x≥80. 解得:10≤x≤35. ∴当且仅当x=10时R取到最大值. ∴OM=10m时,保护区面积最大. 19.(16分)(2014•江苏)已知函数f(x)=ex+e﹣x ,其中e是自然对数的底数. (1)证明:f(x)是R上的偶函数; (2)若关于x的不等式mf(x)≤e﹣x+m﹣1在(0,+∞)上恒成立,求实数m的取值范围; (3)已知正数a满足:存在x0∈[1,+∞),使得f(x0)<a(﹣x03+3x0)成立,试比较ea﹣1与ae﹣1的大小,并证明你的结论. 【分析】(1)根据函数奇偶性的定义即可证明f(x)是R上的偶函数; (2)利用参数分离法,将不等式mf(x)≤e﹣x+m﹣1在(0,+∞)上恒成立,进行转化求最值问题即可求实数m的取值范围; (3)构造函数,利用函数的单调性,最值与单调性之间的关系,分别进行讨论即可得到结论. 【解答】解:(1)∵f(x)=ex+e﹣x, ∴f(﹣x)=e﹣x+ex=f(x),即函数:f(x)是R上的偶函数; (2)若关于x的不等式mf(x)≤e﹣x+m﹣1在(0,+∞)上恒成立, 即m(ex+e﹣x﹣1)≤e﹣x﹣1, ∵x>0, ∴ex+e﹣x﹣1>0, 即m≤在(0,+∞)上恒成立, 设t=ex,(t>1),则m≤在(1,+∞)上恒成立, ∵=﹣=﹣,当且仅当t=2时等号成立, ∴m. (3)令g(x)=ex+e﹣x﹣a(﹣x3+3x), 则g′(x)=ex﹣e﹣x+3a(x2﹣1), 当x>1,g′(x)>0,即函数g(x)在[1,+∞)上单调递增, 故此时g(x)的最小值g(1)=e+﹣2a, 由于存在x0∈[1,+∞),使得f(x0)<a(﹣x03+3x0)成立, 故e+﹣2a<0, 即a>(e+), 令h(x)=x﹣(e﹣1)lnx﹣1, 则h′(x)=1﹣, 由h′(x)=1﹣=0,解得x=e﹣1, 当0<x<e﹣1时,h′(x)<0,此时函数单调递减, 当x>e﹣1时,h′(x)>0,此时函数单调递增, ∴h(x)在(0,+∞)上的最小值为h(e﹣1), 注意到h(1)=h(e)=0, ∴当x∈(1,e﹣1)⊆(0,e﹣1)时,h(e﹣1)≤h(x)<h(1)=0, 当x∈(e﹣1,e)⊆(e﹣1,+∞)时,h(x)<h(e)=0, ∴h(x)<0,对任意的x∈(1,e)成立. ①a∈((e+),e)⊆(1,e)时,h(a)<0,即a﹣1<(e﹣1)lna,从而ea﹣1<ae﹣1, ②当a=e时,ae﹣1=ea﹣1, ③当a∈(e,+∞)⊆(e﹣1,+∞)时,当a>e﹣1时,h(a)>h(e)=0,即a﹣1>(e﹣1)lna,从而ea﹣1>ae﹣1. 20.(16分)(2014•江苏)设数列{an}的前n项和为Sn ,若对任意的正整数n,总存在正整数m,使得Sn=am,则称{an}是“H数列”. (1)若数列{an}的前n项和为Sn=2n(n∈N*),证明:{an}是“H数列”; (2)设{an}是等差数列,其首项a1=1,公差d<0,若{an}是“H数列”,求d的值; (3)证明:对任意的等差数列{an},总存在两个“H数列”{bn}和{cn},使得an=bn+cn(n∈N*)成立. 【分析】(1)利用“当n≥2时,an=Sn﹣Sn﹣1,当n=1时,a1=S1”即可得到an,再利用“H”数列的意义即可得出. (2)利用等差数列的前n项和即可得出Sn,对∀n∈N*,∃m∈N*使Sn=am,取n=2和根据d<0即可得出; (3)设{an}的公差为d,构造数列:bn=a1﹣(n﹣1)a1=(2﹣n)a1,cn=(n﹣1)(a1+d),可证明{bn}和{cn}是等差数列.再利用等差数列的前n项和公式及其通项公式、“H”的意义即可得出. 【解答】解:(1)当n≥2时,an=Sn﹣Sn﹣1=2n﹣2n﹣1=2n﹣1, 当n=1时,a1=S1=2. 当n=1时,S1=a1. 当n≥2时,Sn=an+1. ∴数列{an}是“H”数列. (2)Sn==, 对∀n∈N*,∃m∈N*使Sn=am,即, 取n=2时,得1+d=(m﹣1)d,解得, ∵d<0,∴m<2, 又m∈N*,∴m=1,∴d=﹣1. (3)设{an}的公差为d,令bn=a1﹣(n﹣1)a1=(2﹣n)a1, 对∀n∈N*,bn+1﹣bn=﹣a1, cn=(n﹣1)(a1+d), 对∀n∈N*,cn+1﹣cn=a1+d, 则bn+cn=a1+(n﹣1)d=an,且数列{bn}和{cn}是等差数列. 数列{bn}的前n项和Tn=, 令Tn=(2﹣m)a1,则. 当n=1时,m=1;当n=2时,m=1. 当n≥3时,由于n与n﹣3的奇偶性不同,即n(n﹣3)为非负偶数,m∈N*. 因此对∀n∈N*,都可找到m∈N*,使Tn=bm成立,即{bn}为H数列. 数列{cn}的前n项和Rn=, 令cm=(m﹣1)(a1+d)=Rn,则m=. ∵对∀n∈N*,n(n﹣3)为非负偶数,∴m∈N*. 因此对∀n∈N*,都可找到m∈N*,使Rn=cm成立,即{cn}为H数列. 因此命题得证. 三、附加题(本大题包括选做题和必做题两部分)(一)选择题(本题包括21、22、23、24四小题,请选定其中两个小题作答,若多做,则按作答的前两个小题评分)【选修4-1:几何证明选讲】 21.(10分)(2014•江苏)如图,AB是圆O的直径,C,D是圆O上位于AB异侧的两点,证明:∠OCB=∠D. 【分析】利用OC=OB,可得∠OCB=∠B,利用同弧所对的圆周角相等,即可得出结论. 【解答】证明:∵OC=OB, ∴∠OCB=∠B, ∵∠B=∠D, ∴∠OCB=∠D. 【选修4-2:矩阵与变换】 22.(10分)(2014•江苏)已知矩阵A=,B=,向量=,x,y为实数,若A=B,求x+y的值. 【分析】利用矩阵的乘法,结合A=B,可得方程组,即可求x,y的值,从而求得x+y的值. 【解答】解:∵矩阵A=,B=,向量=,A=B, ∴, ∴x=﹣,y=4, ∴x+y= 【选修4-3:极坐标及参数方程】 23.(2014•江苏)在平面直角坐标系xOy中,已知直线l的参数方程为(t为参数),直线l与抛物线y2=4x相交于A,B两点,求线段AB的长. 【分析】直线l的参数方程化为普通方程,与抛物线y2=4x联立,求出A,B的坐标,即可求线段AB的长. 【解答】解:直线l的参数方程为,化为普通方程为x+y=3, 与抛物线y2=4x联立,可得x2﹣10x+9=0, ∴交点A(1,2),B(9,﹣6), ∴|AB|==8. 【选修4-4:不等式选讲】 24.(2014•江苏)已知x>0,y>0,证明(1+x+y2)(1+x2+y)≥9xy. 【分析】由均值不等式可得1+x+y2≥3,1+x2+y≥,两式相乘可得结论. 【解答】证明:由均值不等式可得1+x+y2≥3,1+x2+y≥ 分别当且仅当x=y2=1,x2=y=1时等号成立, ∴两式相乘可得(1+x+y2)(1+x2+y)≥9xy. (二)必做题(本部分包括25、26两题,每题10分,共计20分) 25.(10分)(2014•江苏)盒中共有9个球,其中有4个红球,3个黄球和2个绿球,这些球除颜色外完全相同. (1)从盒中一次随机取出2个球,求取出的2个球颜色相同的概率P; (2)从盒中一次随机取出4个球,其中红球、黄球、绿球的个数分别记为x1,x2,x3,随机变量X表示x1,x2,x3中的最大数,求X的概率分布和数学期望E(X). 【分析】(1)先求出取2个球的所有可能,再求出颜色相同的所有可能,最后利用概率公式计算即可; (2)先判断X的所有可能值,在分别求出所有可能值的概率,列出分布列,根据数学期望公式计算即可. 【解答】解(1)一次取2个球共有=36种可能,2个球颜色相同共有=10种可能情况 ∴取出的2个球颜色相同的概率P=. (2)X的所有可能值为4,3,2,则P(X=4)=,P(X=3)= 于是P(X=2)=1﹣P(X=3)﹣P(X=4)=, X的概率分布列为 X 2 3 4 P 故X数学期望E(X)=. 26.(10分)(2014•江苏)已知函数f0(x)=(x>0),设fn(x)为fn﹣1(x)的导数,n∈N*. (1)求2f1()+f2()的值; (2)证明:对任意n∈N*,等式|nfn﹣1()+fn()|=都成立. 【分析】(1)由于求两个函数的相除的导数比较麻烦,根据条件和结论先将原函数化为:xf0(x)=sinx,然后两边求导后根据条件两边再求导得:2f1(x)+xf2(x)=﹣sinx,把x=代入式子求值; (2)由(1)得,f0(x)+xf1(x)=cosx和2f1(x)+xf2(x)=﹣sinx,利用相同的方法再对所得的式子两边再求导,并利用诱导公式对所得式子进行化简、归纳,再进行猜想得到等式,用数学归纳法进行证明等式成立,主要利用假设的条件、诱导公式、求导公式以及题意进行证明,最后再把x=代入所给的式子求解验证. 【解答】解:(1)∵f0(x)=,∴xf0(x)=sinx, 则两边求导,[xf0(x)]′=(sinx)′, ∵fn(x)为fn﹣1(x)的导数,n∈N*, ∴f0(x)+xf1(x)=cosx, 两边再同时求导得,2f1(x)+xf2(x)=﹣sinx, 将x=代入上式得,2f1()+f2()=﹣1, (2)由(1)得,f0(x)+xf1(x)=cosx=sin(x+), 恒成立两边再同时求导得,2f1(x)+xf2(x)=﹣sinx=sin(x+π), 再对上式两边同时求导得,3f2(x)+xf3(x)=﹣cosx=sin(x+), 同理可得,两边再同时求导得,4f3(x)+xf4(x)=sinx=sin(x+2π), 猜想得,nfn﹣1(x)+xfn(x)=sin(x+)对任意n∈N*恒成立, 下面用数学归纳法进行证明等式成立: ①当n=1时,成立,则上式成立; ②假设n=k(k>1且k∈N*)时等式成立,即, ∵[kfk﹣1(x)+xfk(x)]′=kfk﹣1′(x)+fk(x)+xfk′(x) =(k+1)fk(x)+xfk+1(x) 又 ===, ∴那么n=k+1(k>1且k∈N*)时.等式也成立, 由①②得,nfn﹣1(x)+xfn(x)=sin(x+)对任意n∈N*恒成立, 令x=代入上式得,nfn﹣1()+fn()=sin(+)=±cos=±, 所以,对任意n∈N*,等式|nfn﹣1()+fn()|=都成立. 参与本试卷答题和审题的老师有:maths;清风慕竹;whgcn;沂蒙松;qiss;caoqz;豫汝王世崇;742048;sxs123;刘长柏;gongjy(排名不分先后) 2017年2月3日查看更多