2017-2018学年辽宁省大连渤海高级中学高二上学期第一次月考数学（文）试题 缺答案

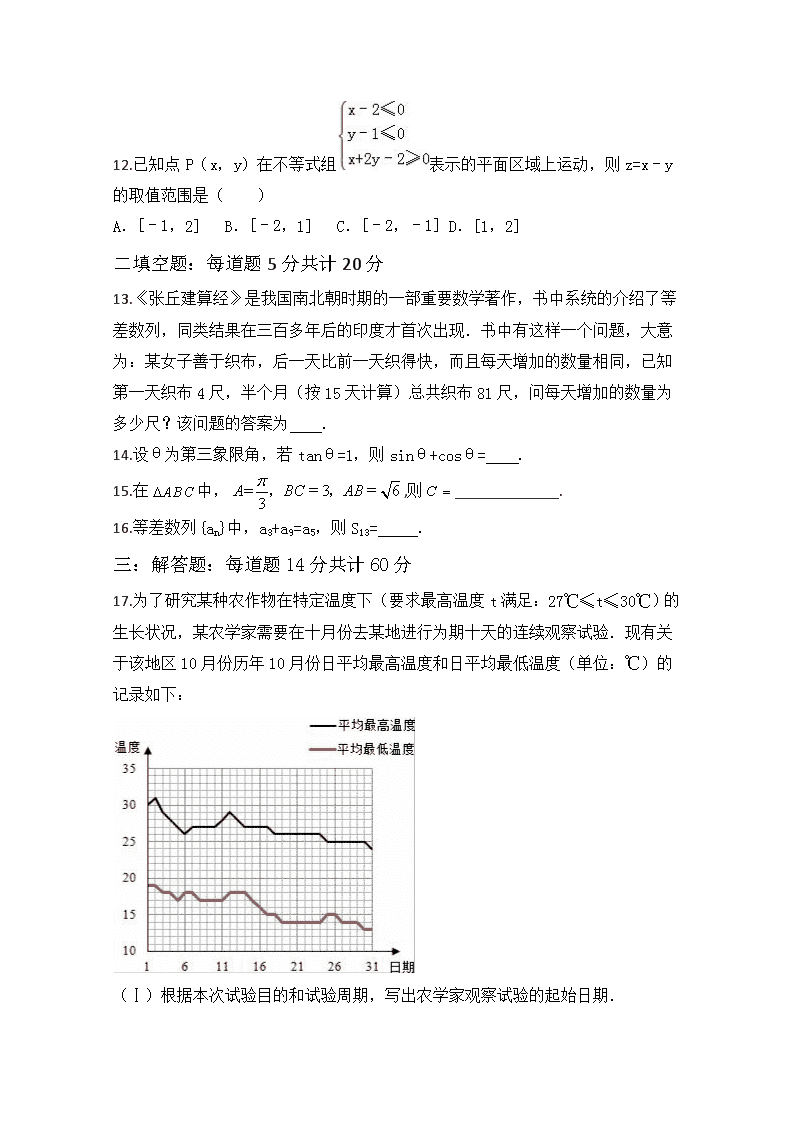
2017-2018学年辽宁省大连渤海高级中学高二上学期第一次月考数学（文）试题 缺答案

‎2017-2018学年辽宁省大连渤海高级中学高二上学期第一次月考数学（文）学科试题 本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。‎ 考查范围：必修3 必修4 必修5全册 考生注意：‎ 1. 答题前，考生务必将自己的条形码贴在答题纸上。‎ 2. 第I卷每小题选出答案后，用2B铅笔把答题纸上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。第Ⅱ卷用黑色墨水签字笔在答题纸上书写作答。在试题卷上作答，答案无效。‎ 第Ⅰ卷 选择题（共60分）‎ 一：选择题：每道题5分，共计60分 ‎1. 下列命题中是真命题的是（　　）‎ A．第二象限的角比第一象限的角大 B．角α是第四象限角的充要条件是2kπ﹣＜α＜2kπ（k∈Z）‎ C．第一象限的角是锐角 D．三角形的内角是第一象限角或第二象限角- ‎2.四名同学根据各自的样本数据研究变量x，y之间的相关关系，并求得回归直线方程，分别得到以下四个结论：①y与x负相关且=2.347x﹣6.423； ②y与x负相关且=﹣3.476x+5.648； ③y与x正相关且=5.437x+8.493； ④y与x正相关且=﹣4.326x﹣4.578． ‎ 其中一定不正确的结论的序号是（　　） ‎ A．①② B．②③ C．③④ D．①④‎ ‎3.若甲、乙、丙三组人数分别为18，24，30，现用分层抽样方法从甲、乙、丙三组中共抽取12人，则在乙组中抽取的人数为（　　）‎ A．3 B．4 C．5 D．6‎ ‎4.‎ 某奶茶店的日销售收入y（单位：百元）与当天平均气温x（单位：℃）之间的关系如下：‎ x ‎﹣2‎ ‎﹣1‎ ‎0‎ ‎1‎ ‎2‎ y ‎5‎ ‎2‎ ‎2‎ ‎1‎ 通过上面的五组数据得到了x与y之间的线性回归方程： =﹣x+2.8；但现在丢失了一个数据，该数据应为（　　）‎ A．3 B．4 C．5 D．2‎ ‎5.用秦九韶算法计算多项式当x=2时v3的值为(　　)‎ A．0 B．－32 C． 80 D． －80‎ ‎6.sin210°=（　　）‎ A． B． C．﹣ D．﹣‎ ‎7.已知tan（π﹣α）=﹣，且α∈（﹣π，﹣），则的值为（　　）‎ A． B． C． D．‎ ‎8.已知平面向量，，且，则=（　　）‎ A．（﹣1，2） B．（1，2） C．（1，﹣2） D．（﹣1，﹣2）‎ ‎9.已知，且，则等于 ‎ A. B. C. D. ‎ ‎10.下面结论正确的是（　　）‎ A．若a＞b，则有 B．若a＞b，则有a|c|＞b|c|‎ C．若a＞b，则有|a|＞b D．若a＞b，则有 ‎11.不等式x2﹣2x＜0的解集是（　　）‎ A．{x|0＜x＜2} B．{x|﹣2＜x＜0} C．{x|x＜0，或x＞2} D．{x|x＜﹣2，或x＞0}‎ ‎12.已知点P（x，y）在不等式组表示的平面区域上运动，则z=x﹣y的取值范围是（　　）‎ A．[﹣1，2] B．[﹣2，1] C．[﹣2，﹣1] D．[1，2]‎ 二填空题：每道题5分共计20分 ‎13.《张丘建算经》是我国南北朝时期的一部重要数学著作，书中系统的介绍了等差数列，同类结果在三百多年后的印度才首次出现．书中有这样一个问题，大意为：某女子善于织布，后一天比前一天织得快，而且每天增加的数量相同，已知第一天织布4尺，半个月（按15天计算）总共织布81尺，问每天增加的数量为多少尺？该问题的答案为　　．‎ ‎14.设θ为第三象限角，若tanθ=1，则sinθ+cosθ=　　．‎ ‎15.在中，,则_____________.‎ ‎16.等差数列{an}中，a3+a9=a5，则S13=　 　．‎ 三：解答题：每道题14分共计60分 ‎17.为了研究某种农作物在特定温度下（要求最高温度t满足：27℃≤t≤30℃）的生长状况，某农学家需要在十月份去某地进行为期十天的连续观察试验．现有关于该地区10月份历年10月份日平均最高温度和日平均最低温度（单位：℃）的记录如下：‎ ‎（Ⅰ）根据本次试验目的和试验周期，写出农学家观察试验的起始日期．‎ ‎（Ⅱ）设该地区今年10月上旬（10月1日至10月10日）的最高温度的方差和最低温度的方差分别为D1，D2，估计D1，D2的大小？（直接写出结论即可）．‎ ‎（Ⅲ）从10月份31天中随机选择连续三天，求所选3天每天日平均最高温度值都在[27，30]之间的概率．‎ ‎18.设等差数列{an}第10项为24，第25项为﹣21．‎ ‎（1）求这个数列的通项公式；‎ ‎（2）设Sn为其前n项和，求使Sn取最大值时的n值．‎ ‎19.（1）解不等式 ‎（2）已知x＞0，y＞0，且x+y=1，求 + 的最小值．‎ ‎20.（12分）已知数列{an}中，an2+2an﹣n2+2n=0（n∈N+）‎ ‎（Ⅰ）求数列{an}的通项公式 ‎（Ⅱ）求数列{an}的前n项和Sn ‎21.在△ABC中，角A，B，C的对边分别为a，b，c，且bcosC=（2a﹣c）cosB．‎ ‎（Ⅰ）求角B的大小；‎ ‎（Ⅱ）若a，b，c成等差数列，且b=3，试求△ABC的面积．‎