2019届二轮复习选择填空标准练(5)作业（全国通用）

2019届二轮复习选择填空标准练(5)作业（全国通用）

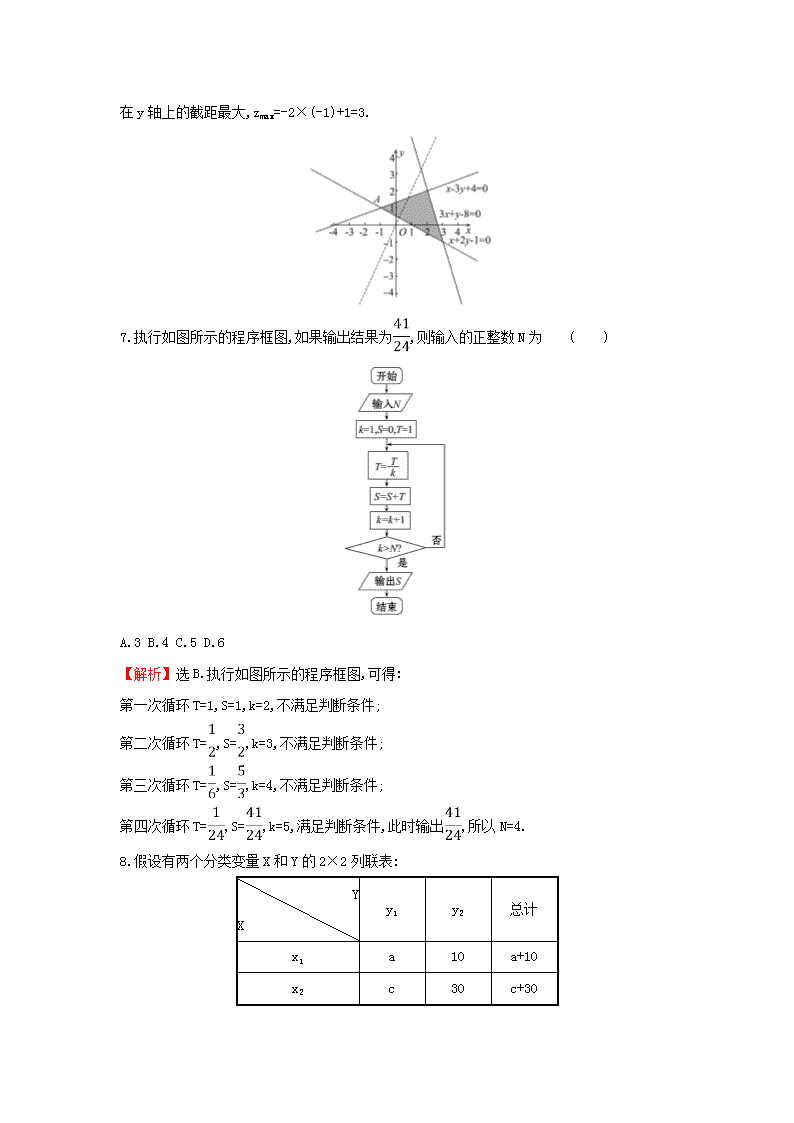
‎2019届二轮复习 选择填空标准练 (5) 作业（全国通用）‎ 一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)‎ ‎1.设集合M={x|-1≤x<2},N={x|x-k≥0},若M⊆N,则k的取值范围是 (　　)‎ A.k≥-1 B.k>-1‎ C.k≤-1 D.k<-1‎ ‎【解析】选C.由题意可知:N={x|x≥k},结合M⊆N可得:k的取值范围是k≤-1.‎ ‎2.已知复数z=,则z= (　　)‎ A. B‎.2 ‎ C. D.5‎ ‎【解析】选D.z====2-i.‎ z=|z|2=22+(-1)2=5.‎ ‎3.已知等差数列{an}的公差不为0,a1=1,且a2,a4,a8成等比数列,设{an}的前n项和为Sn,则Sn= (　　)‎ A. B.‎ C. D.‎ ‎【解析】选A.设等差数列{an}的公差为d.因为a2,a4,a8成等比数列,‎ 所以=a2·a8,即(a1+3d)2=(a1+d)·(a1+7d),所以(1+3d)2=(1+d)·(1+7d),‎ 解得d=1.所以Sn=n+=.‎ ‎4.一个四面体的顶点在空间直角坐标系O-xyz中的坐标分别是(0,0,0),(1,0,1), (0,1,1),,1,0,绘制该四面体三视图时,按照如图所示的方向画正视图,则得到侧视图可以为 (　　)‎ ‎【解析】选C.满足条件的四面体如图:‎ 依题意投影到yOz平面为正投影,所以侧视方向如图所示,所以得到侧视图效果如图.‎ ‎5.已知a>b,则“c≥‎0”‎是“ac>bc”的 (　　)‎ A.充分不必要条件 B.必要不充分条件 C.充分必要条件 D.既不充分又不必要条件 ‎【解析】选B.当时,ac>bc不成立,所以充分性不成立,当时,c>0成立,c≥0也成立,所以必要性成立,所以“c≥0”是“ac>bc”的必要不充分条件.‎ ‎6.若x,y满足约束条件则z=-2x+y 的最大值是 (　　)‎ A.-7 B.‎-2 ‎ C.3 D.4‎ ‎【解析】选C.由约束条件 作出可行域如图所示,联立 解得A(-1,1),化z=-2x+y为y=2x+z,由图可知,当直线y=2x+z过A(-1,1)时,直线y=2x+z在y轴上的截距最大,zmax=-2×(-1)+1=3.‎ ‎7.执行如图所示的程序框图,如果输出结果为,则输入的正整数N为 (　　)‎ A.3 B‎.4 ‎C.5 D.6‎ ‎【解析】选B.执行如图所示的程序框图,可得:‎ 第一次循环T=1,S=1,k=2,不满足判断条件;‎ 第二次循环T=,S=,k=3,不满足判断条件;‎ 第三次循环T=,S=,k=4,不满足判断条件;‎ 第四次循环T=,S=,k=5,满足判断条件,此时输出,所以N=4.‎ ‎8.假设有两个分类变量X和Y的2×2列联表:‎ Y X y1‎ y2‎ 总计 x1‎ a ‎10‎ a+10‎ x2‎ c ‎30‎ c+30‎ 总计 ‎60‎ ‎40‎ ‎100‎ 注:K2=‎ ‎=n-·-.‎ 对同一样本,以下数据能说明X和Y有关系的可能性最大的一组为 (　　)‎ A.a=45,c=15 B.a=40,c=20‎ C.a=35,c=25 D.a=30,c=30‎ ‎【解析】选A.根据独立性检验的方法和2×2列联表可得,‎ K2=100,K2越大,有关系的可能性越大,由各选项可得A满足条件.‎ ‎9.下列关于函数f(x)=sin x(sin x+cos x)的说法中,错误的是 (　　)‎ A.f(x)的最小正周期为π B.f(x)的图象关于点,0对称 C.f(x)的图象关于直线x=-对称 D.f(x)的图象向右平移个单位后得到一个偶函数的图象 ‎【解析】选B.因为f(x)=sin x(cos x+sin x)‎ ‎=sin 2x+‎ ‎=sin2x-+,‎ 所以f(x)的最小正周期T==π,故A正确;‎ 由f=sin2×-+=,故B错误;‎ 由sin=-1,故C正确;‎ 将f(x)的图象向右平移个单位后得到y=sin2x--+=-cos ‎ 2x,为偶函数,故D正确.‎ ‎10.已知数列{an}满足当1≤n≤3时,an=n,且对∀n∈N*,有an+3+an+1=an+2+an,则数列{n·an}的前50项的和为 (　　)‎ A.2 448 B.2 525‎ C.2 533 D.2 652‎ ‎【解析】选B.由题得an+3+an+1=an+2+an=…=a3+a1=4,所以an=4-an+2=4-(4-an+4)=an+4,‎ 所以数列{an}是周期为4的周期数列,且a1=1,a2=2,a3=3,a4=2.所以a1+‎2a2+‎3a3+‎4a4+‎5a5+…+‎50a50=(1+5+9+…+49)+2(2+4+6+8+…+50)+3(3+7+11+…+47)=2 525.‎ ‎11.若函数f(x)=2exln(x+m)+ex-2存在正的零点,则实数m的取值范围 为 (　　)‎ A.(e,+∞) B.(,+∞) ‎ C.(-∞,e) D.(-∞,)‎ ‎【解析】选D.由f(x)=2exln(x+m)+ex-2=0,‎ 可得ln(x+m)=-,‎ 令g(x)=ln(x+m)-,‎ 易知g(x)为增函数.‎ 因为函数f(x)=2exln(x+m)+ex-2存在正的零点,所以g(0)<0,所以ln m<,‎ 所以00)上,则双曲线C的渐近线方程为________. ‎ ‎【解析】由于双曲线关于原点对称,故(-2,1),(2,-1)在双曲线上,代入方程解得a=,又因为b=1,所以渐近线方程为y=±x.‎ 答案:y=±x ‎15.在四棱锥S-ABCD中,SD⊥底面ABCD,底面ABCD是正方形,SD=AD=2,三棱柱MNP-M1N1P1的顶点都位于四棱锥S-ABCD的棱上,已知M,N,P分别是棱AB,AD,AS的中点,则三棱柱MNP-M1N1P1的体积为________.  ‎ ‎【解析】由题得M1是BC中点,N1是DC中点,P1是SC中点,PN=1,MN=,且PN⊥‎ MN,所以三棱柱MNP-M1N1P1的底面积为×1×=.‎ 由题得正方形的对角线长2,三棱柱MNP-M1N1P1的高为×2=,‎ 所以三棱柱MNP-M1N1P1的体积为×=1.‎ 答案:1‎ ‎16.设α1,α2∈R,且+=2,则 ‎|10π-α1-α2|的最小值等于________.  ‎ ‎【解析】由三角函数的性质可知∈,∈,‎ ‎ 所以==1,‎ 即sin α1=sin(2α2)=-1,‎ 所以α1=-+2kπ,α2=-+lπ,k,l∈Z,‎ α1+α2=-+(2k+l)π,2k+l∈Z,从而10π-α1-α2=10π+-(2k+l)π,‎ 所以2k+l=11时,|10π-α1-α2|min=.‎ 答案:‎