2018-2019学年福建省霞浦第一中学高二下学期第一次月考数学（理）试题 解析版

2018-2019学年福建省霞浦第一中学高二下学期第一次月考数学（理）试题 解析版

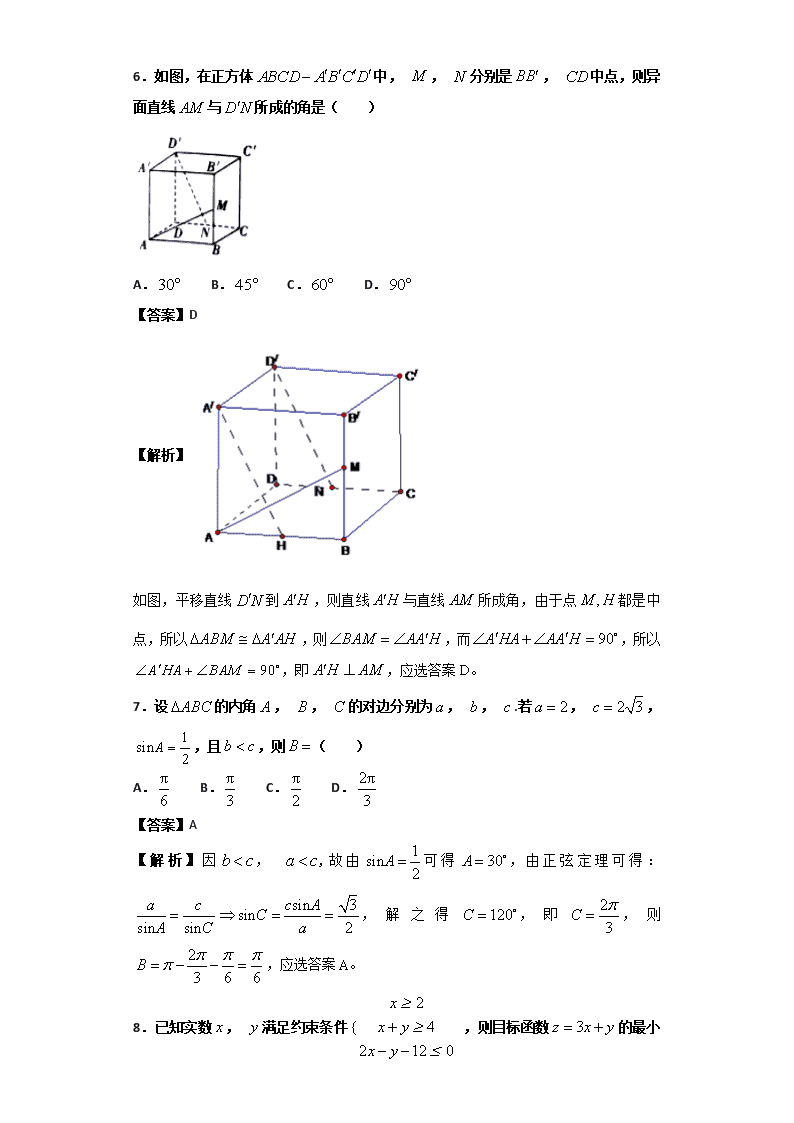
绝密★启用前 福建省霞浦第一中学 2018-2019 学年高二下学期第一次月考 数学（理)试题 评卷人 得分 一、单选题 1．命题“ R， ”的否定是( ) A． R， B． R， C． R， D． R， 【答案】D 【解析】 【分析】 利用全称命题的否定是特称命题分析解答. 【详解】 由题得命题“ R， ”的否定是“ R， ”. 故答案为：D 【点睛】 本题主要考察全称命题和特称命题的否定，意在考察学生对这些基础知识的理解和掌握 水平. 2．在空间直角坐标系 O xyz 中，点  2,4, 3P   关于 yOz 平面的对称点的坐标为 （ ） A． 2,4, 3 B． 2, 4,3  C． 2, 4, 3  D． 2,4,3 【答案】A 【解析】依据空间直角坐标系中点的对称性可知：点  2,4, 3P   关于 yOz 平面的对 称点的坐标为 2,4, 3 ，应选答案 A。 3．设 a ， b ， c R ，且 0b a  ，则（ ） A． ac bc B． 2 2ac bc C． 1 1 a b  D． 1a b  【答案】C 【解析】若 0c  ，则 ac bc 不成立，故答案 A 错误；若 0c  ，则 2 2ac bc 不成立， 故答案 B 错误；因为 0b a  ，所以 0ab  ，则由不等式的性质对不等式 0b a  两 边同乘以 1 ab 可得 b a ab ab  ，即 1 1 a b  ，故答案 C 正确；若 2, 3 1aa b b       ， 则答案 D 不正确，应选答案 C。 4．正项等比数列 na 中， 4 5 32a a  ，则 2 1 2 2 2 8log log loga a a   的值（ ） A．10 B．20 C．36 D．128 【答案】B 【 解 析 】 由 等 比 数 列 的 性 质 可 知 1 8 2 7 3 6 4 5 32a a a a a a a a    ， 所 以 2 1 2 2 2 8log log loga a a        4 2 1 8 2 7 3 6 4 5 2log 32 4 5 20a a a a a a a a log     ，应选答案 B。 5．如图，在平行六面体 中， 为 与 的交点.若 ， ， ，则下列向量中与 相等的向量是( ) A． B． C． D． 【答案】B 【解析】 【分析】 连接 ,由平行四边形法则得到 ，再得到 . 【详解】 连接 ,因为 M 是 中点， 所以 . 故答案为：B 【点睛】 本题主要考察平面向量的加法、减法和平行四边形法则，意在考察学生对这些知识的理 解能力和掌握水平. 6．如图，在正方体 ABCD A B C D    中， M ， N 分别是 BB ， CD 中点，则异 面直线 AM 与 D N 所成的角是（ ） A．30 B． 45 C． 60 D．90 【答案】D 【解析】 如图，平移直线 D N 到 A H ，则直线 A H 与直线 AM 所成角，由于点 ,M H 都是中 点，所以 ABM A AH    ，则 BAM AA H    ，而 90A HA AA H     ，所以 90A HA BAM     ，即 A H AM  ，应选答案 D。 7．设 ABC 的内角 A ， B ， C 的对边分别为 a ， b ， c .若 2a  ， 2 3c  ， 1sin 2A  ，且b c ，则 B  （ ） A． π 6 B． π 3 C． π 2 D． 2π 3 【答案】A 【 解 析 】 因 b c ， a c , 故 由 1sin 2A  可 得 30A   ， 由 正 弦 定 理 可 得 ： sin 3sinsin sin 2 a c c ACA C a     ， 解 之 得 120C   ， 即 2 3C  ， 则 2 3 6 6B       ，应选答案 A。 8．已知实数 x ， y 满足约束条件 2 { 4 2 12 0 x x y x y       ，则目标函数 3z x y  的最小 值为（ ） A． 8 B． 2 C．8 D． 44 3 【答案】C 【解析】 画出不等式组 2 { 4 2 12 0 x x y x y       表示的区域如图，结合图形可知当动直线 3y x z   经过点  2,2A 时，动直线在 y 轴上的截距 z 最小， min 3 2 2 8z     ，应选答案 C。 9．已知椭圆 : 内有一条以点 为中点的弦 ，则直线 的方程为 ( ) A． B． C． D． 【答案】C 【解析】 【分析】 设 ， ， ， ，则由中点坐标公式可求 ， ，由 ， 在椭圆上 可 得 ， ，两式相减可得，结合 ，代入可求直线 的斜率， 进而可求直线 的方程. 【详解】 设 ， ， ， ，则 ， 由 ， 在椭圆上可得 ， , 两式相减可得， 直线 的方程为 即 故答案为： 【点睛】 本题主要考查了解析几何中的点差法和设而不求，意在考查学生对这些知识的理解 能力掌握水平和应用能力. 10．已知双曲线 的两条渐近线与抛物线 的准线分 别交于 ， 两点．若双曲线 的离心率为 ， 的面积为 ， 为坐标原点，则抛物 线的焦点坐标为 ( ) A． B． C． D． 【答案】B 【解析】 【分析】 求出双曲线双曲线 （a＞0，b＞0）的渐近线方程与抛物线 y2＝2px（p＞0）的 准线方程，进而求出 A，B 两点的坐标，再由双曲线的离心率为 2，△AOB 的面积为 ， 列出方程，由此方程求出 p 的值． 【详解】 ∵双曲线 （a＞0，b＞0）， ∴双曲线的渐近线方程是 y＝± x 又抛物线 y2＝2px（p＞0）的准线方程是 x ， 故 A，B 两点的纵坐标分别是 y＝± ， 又由双曲线的离心率为 2，所以 2，则 ， A，B 两点的纵坐标分别是 y＝± ，即 = , 又△AOB 的面积为 ，且 轴， ∴ ，得 p＝2． 抛物线的焦点坐标为：（1，0） 故选：B． 【点睛】 本题考查圆锥曲线的共同特征，解题的关键是求出双曲线的渐近线方程，解出 A，B 两 点的坐标，列出三角形的面积与离心率的关系也是本题的解题关键，有一定的运算量， 做题时要严谨． 11．《九章算术》中对已知三角形三边长求三角形面积的求法填补了我国传统数学的空 白，与著名的海伦公式完全等价，由此可以看出我国古代已具有很高的数学水平，其求 法是：“以小斜幂并大斜幂减中斜幂，余半之,自乘于上.以小斜幂乘大斜幂减上，余四约 之 ， 为 实 . 一 为 从 隔 ， 开 平 方 得 积 .” 若 把 以 上 这 段 文 字 写 出 公 式 ， 即 22 2 2 2 21 4 2 c a bS c a            . 现 有 周 长 2 2 5 的 ABC 满 足 sin :sin :sinA B C     2 1 : 5 : 2 1  ，试用以上给出的公式求得的面积为（ ） A． 3 4 B． 3 2 C． 5 4 D． 5 2 【答案】A 【 解 析 】 由 正 弦 定 理 及 题 设 可 设 三 角 形 的 三 边 分 别 为    2 1 , 5 , 2 1a x b x c x     ， 由 题 意    2 1 5 2 1 2 2 5x x x      ，则 1x  ，故由三角形的面积公式可得：     2 2 21 3 2 2 3 2 2 5 3[ 2 1 2 14 2 4S             ，应选答案 A。 12．如图，在四棱锥 中， 平面 ， ， ， ， ，点 满足 ，动点 在平面 内，若 ，则点 的轨迹是( ) A．圆 B．椭圆 C．双曲线 D．抛物线 【答案】D 【解析】 【分析】 以点 C 为坐标原点，以 CB 所在直线作 x 轴，以 CP 所在直线作 y 轴，以 CD 所在直线 为 z 轴，建立空间直角坐标系. 设 M(x,y,0),求得 ，再 利用向量的夹角公式求得 ，即得点 M 的轨迹. 【详解】 由题得 AD=DG, 以点 C 为坐标原点，以 CB 所在直线作 x 轴，以 CP 所在直线作 y 轴，以 CD 所在直线 为 z 轴，建立空间直角坐标系.则 B(2,2,0),G(-1,0, ),设 M(x,y,0), 则 ， 所以 ， 化简得 ，所以点 M 的轨迹是抛物线. 故答案为：D 【点睛】 本题主要考查空间向量、空间角的计算和立体几何中的轨迹问题，意在考查学生对这些 知识的理解和掌握水平及应用能力.解答本题的关键是想到建立空间直角坐标系解决问 题. 第 II 卷（非选择题) 请点击修改第 II 卷的文字说明 评卷人 得分 二、填空题 13．已知 ， ，若 是 的充分不必要条件，则实数 的取值范围是 ________. 【答案】 【解析】 【分析】 直接利用充分不必要的性质得到 k≤0. 【详解】 因为 是 的充分不必要条件，所以 k≤0. 故答案为： 【点睛】 本题主要考查充分必要条件的应用，意在考查学生对这些知识的理解能力掌握水平和应 用能力. 14．若关于 x 的不等式   21 1 0m x mx m     的解集为  ，则 m 的取值范围为 __________． 【答案】 2 3,3    【解析】由题设可得  2 2 1 0 { 4 1 0 m m m      ，解之得 2 3 3m  ，应填答案 2 3 ,3     。 15．已知数列 na 满足    1 1 n n na a n    ，则 na 的前 40 项和为__________． 【答案】 220 【 解 析 】 由 题 设    1 1 n n na a n    可 得    1 1 1n n n na a n     ， 分 别 赋 值 1,2,3,4,5, ,40n   ， 可 得 2 1 3 2 4 3 5 4 6 5 40 39+ 1, 2, 3, 4, 5, , 39a a a a a a a a a a a a                ，所 以 1 3 4 2 3 5 6 4 5 7 6 8 7 9 8 101, 5, 1, 9, 1, 13, 1, 17, .a a a a a a a a a a a a a a a a                     由此可以看出：数列的相邻两奇数项之和均为1；相邻两偶数项之和构成以为 5 首项公 差 为 4 的 等 差 数 列 ， 所 以 该 数 列 前 40 项 和 为    40 10 910 1 10 5 4 2202S           ，应填答案 220 。 点睛：解答本题的关键是先借助题设条件对正整数 n 进行赋值 1,2,3,4,5, ,40n   ， 从 而 得 到 2 1 3 2 4 3 5 4 6 5 40 39+ 1, 2, 3, 4, 5, , 39a a a a a a a a a a a a                ，进 而 通 过 观 察 计 算 得 到 1 3 4 2 3 5 6 4 5 7 6 8 7 9 8 101, 5, 1, 9, 1, 13, 1, 17, .a a a a a a a a a a a a a a a a                     获得了结论“数列的相邻两奇数项之和均为1；相邻两偶数项之和构成以为 5 首项公差 为 4 的 等 差 数 列 ” ， 最 后 求 出 该 数 列 前 40 项 和 为    40 10 910 1 10 5 4 2202S           。 16．已知 是抛物线 上的动点， 为抛物线的焦点，点 在圆 : 上，则 的最小值为___________. 【答案】2 【解析】 【分析】 画出图形，利用抛物线的定义以及性质，转化求解 最小值． 【详解】 经过 作抛物线的准线的垂线 ，垂足为 ，如图：由抛物线的定义可知： ， 当 、 、 经过圆的圆心时， 取得最小值， 圆心 ，半径为 1，所以 最小值为：2． 故答案为：2． 【点睛】 本题考查准线与抛物线的位置关系的综合应用，圆的方程的应用，考查计算能力． 评卷人 得分 三、解答题 17．已知抛物线 的准线方程为 . （Ⅰ）求 的值； （Ⅱ）直线 交抛物线于 、 两点，求弦长 . 【答案】（Ⅰ）2；（Ⅱ）8. 【解析】 【分析】 （Ⅰ）依已知得 ，所以 ；（Ⅱ）设 ， ，由 消去 ， 得 ,再利用韦达定理求弦长 . 【详解】 （Ⅰ）依已知得 ，所以 ； （Ⅱ）设 ， ，由 消去 ，得 ， 则 ， ， 所以 . 【点睛】 本题主要考查抛物线的简单几何性质和弦长的计算，意在考查学生对这些知识的理解能 力掌握水平及其应用能力. 18．已知等差数列 的前 项和为 ，且满足 ， . （1）求 的通项公式； （2）求 的值. 【答案】（1） （2） 【解析】 【分析】 （1）直接利用已知条件求出数列的通项公式；（2）根据数列的通项公式，进一步利用 裂项相消法求出数列的和． 【详解】 (1)设等差数列 的公差为 ，由 ，得 ， 则有 ，所以 ，故 . (2)由(1)知， ，则 ， 所以 . 【点睛】 本题主要考查了等差数列的概念，以及数列的求和，属于高考中常考知识点，难度不大； 常见的数列求和的方法有公式法即等差等比数列求和公式，分组求和类似于 ，其中 和 分别为特殊数列，裂项相消法类似于 ，错位 相减法类似于 ，其中 为等差数列， 为等比数列等. 19．在 中，边 ， ，分别是角 ， ， 的对边，且满足等式 . （Ⅰ）求角 的大小； （Ⅱ）若 ，且 ，求 . 【答案】（Ⅰ） （Ⅱ） 【解析】 试题分析：（1）题设中的条件是边角的关系，利用正弦定理把它转化为角的三角关系 ，化简可得 ，从而求出 .（2）中 利用构建关于 的关系式， ，配凑后得到 . 解析：(1)由 ，得 ，则 ，因为 ,所以 ，因为 ,所以 . (2)由 , 得 ,由余弦定理得 ，且 得 ，即 ,所以 . 20．漳州市博物馆为了保护一件珍贵文物，需要在馆内一种透明又密封的长方体玻璃保 护罩内充入保护液体.该博物馆需要支付的总费用由两部分组成：①罩内该种液体的体 积比保护罩的容积少 0.5 立方米，且每立方米液体费用 500 元；②需支付一定的保险 费用，且支付的保险费用与保护罩容积成反比，当容积为 2 立方米时，支付的保险费用 为 4000 元. （Ⅰ）求该博物馆支付总费用 y 与保护罩容积 x 之间的函数关系式； （Ⅱ）求该博物馆支付总费用的最小值. 【答案】（Ⅰ） 8000500 250y x x    （Ⅱ）博物馆支付总费用的最小值为 3750 元 【解析】【试题分析】（1）先依据题设分别求出支付的保险费用 1 8000y x  和保护液体 的 费 用  500 0.5x  ， 再 求 出 运 总 费 用 y 与 保 护 罩 容 积 x 之 间 的 函 数 关 系 式 8000500 250y x x    ，（ 0.5x  ）；（2）依据题设条件运用基本不等式求出 8000500x x  的最小值，从而确定函数 8000500 250y x x    的最小值： 解：（Ⅰ）由题意设支付的保险费用 1 ky x  ，把 2x  ， 1 4000y  代入，得 8000k  . 则有支付的保险费用 1 8000y x  （ 0.5x  ） 故总费用   8000 8000500 0.5 500 250y x xx x       ，（ 0.5x  ） （Ⅱ）因为 8000500 250y x x    80002 500 250 3750x x    当且仅当 8000500x x  且 0.5x  ， 即 4x  立方米时不等式取等号， 所以，博物馆支付总费用的最小值为 3750 元. 点睛：求解本题的第一问时，先依据题设条件运用待定系数法求出支付的保险费用 1 8000y x  ，再求出保护液体的费用  500 0.5x  ，进而求出运总费用 y 与保护罩容积 x 之间的函数关系式 8000500 250y x x    ，（ 0.5x  ）；求解第二问时，重点是依 据 题 设 条 件 运 用 基 本 不 等 式 先 求 出 8000500x x  的 最 小 值 ， 从 而 确 定 函 数 8000500 250y x x    的最小值及取得最小值时 x 的值，从而使得问题获解。 21．如图，在三棱柱 中，侧面 为菱形， ， ， . （Ⅰ）求证： ； （Ⅱ）若 ，求二面角 的余弦值. 【答案】（Ⅰ）详见解析；（Ⅱ） . 【解析】 【分析】 （Ⅰ）过点 作 于点 ，连接 ， ，则 为 的中点.证明 即可. （Ⅱ）以 为原点，以 ， ， 为 轴， 轴， 轴建立空间直角坐标系，利 用向量法求二面角 的余弦值. 【详解】 （Ⅰ）过点 作 于点 ，连接 ， ，则 为 的中点. 侧面 为菱形且 ， ，∴ 又 ∴ . （Ⅱ）以 为原点，以 ， ， 为 轴， 轴， 轴建立空间直角坐标系， 则 ， ， ， , ， ， 设平面 法向量为 则 即 得 取 ，得 ， 设平面 法向量为 则 即 ， 得 取 ，得 ， ， ， 又∵二面角 为钝角 ∴二面角 的余弦值为 【点睛】 （1）本题主要考查空间几何元素位置关系的证明和空间角的计算，意在考查学生对这 些知识的理解能力掌握水平和分析推理计算能力.(2)证明空间几何元素的位置关系一般 利用转化证明法，求空间的角一般用几何法和向量法. 22．已知椭圆 的短轴长等于 ，离心率为 ， 、 分别为椭 圆 的上、下顶点. （Ⅰ）求椭圆 的方程； （Ⅱ）设 为直线 不同于点 的任意一点，若直线 、 分别与椭圆相交于异 于 、 的点 、 ，证明： 恒为钝角. 【答案】（Ⅰ） ；（Ⅱ）详见解析. 【解析】 【分析】 （Ⅰ）直接根据已知得到关于 a,b,c 的方程解方程组即得椭圆 的方程；（Ⅱ）设 ，求出 ，再利用 得到 为锐角， 又 与 互补，所以 恒为钝角. 【详解】 （Ⅰ）由椭圆的短轴长等于 ，所以 ，解得 ， 又因为椭圆的离心率为 ，所以 ，解得 ， 所以椭圆 的方程是 ； （Ⅱ）设 ，则直线 ，代入椭圆 的方程中， 整理得 ， 解得 ，或 ， 所以 ， 所以 ， 又 ，所以 ， 又 、 、 三点不共线，所以 为锐角， 又 与 互补，所以 恒为钝角. 【点睛】 本题主要考查椭圆的简单几何性质和方程的求法，考查直线和椭圆的位置关系和向量的 夹角的性质，意在考查学生对这些知识的理解能力掌握水平和分析推理计算能力.