2019届高三数学上学期月考试题(一)文(含解析)
2019届高三数学上学期月考试题(一)文(含解析)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共8页。时量120分钟。满分150分。
第Ⅰ卷
一、选择题:本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.函数f(x)=的定义域是(A)
A. B.∪
C. D.∪
【解析】解不等式6-x-x2>0得(x-2)(x+3)<0x∈.选A.
2.已知复数z=,给出下列四个结论:①|z|=2;②z2=2i;③z的共轭复数=-1+i;④z的虚部为i.其中正确结论的个数是(B)
A.0 B.1 C.2 D.3
【解析】由已知z=1+i,则|z|=,z2=2i,=1-i,z的虚部为1.所以仅结论②正确,选B.
3.已知命题p:若a>,则a2>b2;命题q:若x2=4,则x=2.下列说法正确的是(A)
A.“p∨q”为真命题 B.“p∧q”为真命题
C.“綈p”为真命题 D.“綈q”为假命题
【解析】由条件可知命题p为真命题,q为假命题,所以“p∨q”为真命题,故选择A.
4.如图,已知=a,=b,=4,=3,则=(D)
A.b-a, B.a-b,
C.a-b, D.b-a,
【解析】=+=+=(--=b-a.选D.
5.如果把直角三角形的三边都增加同样的长度,则得到的这个新三角形的形状为(A)
A.锐角三角形 B.直角三角形
C.钝角三角形 D.由增加的长度决定
【解析】设增加同样的长度为x,原三边长为a、b、c,且c2=a2+b2,a+b>c.新的三角形的三边长为a+x、b+x、c+x,知c+x为最大边,其对应角最大.而(a+x)2+(b+x)2-(c+x)2=x2+2(a+b-c)x>0,由余弦定理知新的三角形的最大角的余弦为正,则为锐角,那么它为锐角三角形.故选A.
6.与直线2x-y+4=0的平行的抛物线y=x2的切线方程是(D)
A.2x-y+3=0 B.2x-y-3=0
C.2x-y+1=0 D.2x-y-1=0
【解析】设P(x0,y0)为切点,则切点的斜率为y′|x=x0=2x0=2,∴x0=1.由此得到切点(1,1).故切线方程为y-1=2(x-1),即2x-y-1=0,故选D.
10
7.右边茎叶图表示的是甲、乙两人在5次综合测评中的成绩(成绩为整数),其中一个数字被污损,则乙的平均成绩不低于甲的平均成绩的概率为(D)
A. B. C. D.
【解析】记其中被污损的数字为x.依题意得甲的5次综合测评的平均成绩为90,乙的5次综合测评的平均成绩为(442+x),令(442+x)≥90,由此解得x≥8,即x的可能取值为8和9,由此乙的平均成绩不低于甲的平均成绩的概率为=,故选D.
8.将函数y=3sin的图象向右平移个单位,所得图象对应的函数(A)
A.在区间上单调递增 B.在区间上单调递减
C.在区间上单调递增 D.在区间上单调递减
【解析】将函数y=3sin的图象向右平移个单位,所得函数变为y=3sin,令2kπ-≤2x-≤2kπ+(k∈Z),解得kπ+≤x≤kπ+(k∈Z),令k=0,≤x≤.故函数在区间上单调递增,故选A.
9.设f(x)=则不等式f(x)>2的解集为(C)
A.(1,2)∪(3,+∞) B.(,+∞)
C.(1,2)∪(,+∞) D.(1,2)
【解析】令2ex-1>2,解得1
2,解得x为,不等式f(x)>2的解集为(1,2)∪(,+∞),故选C.
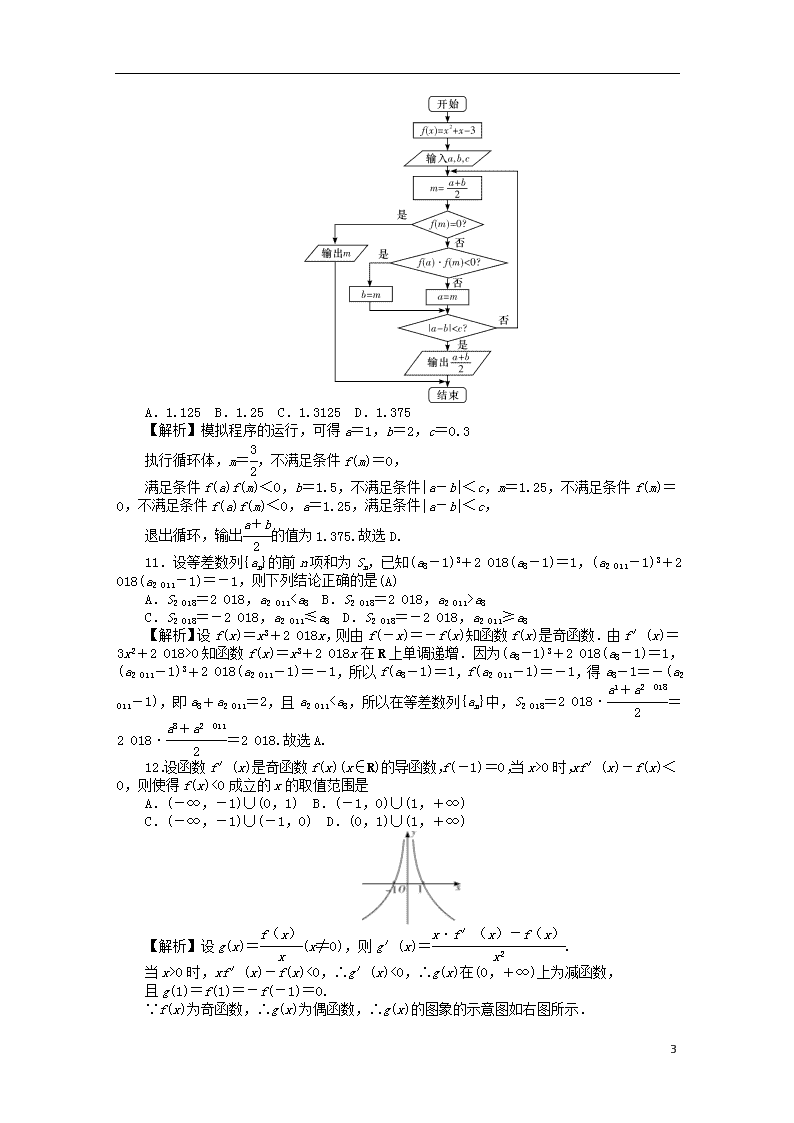
10.执行如图所示的程序框图,若输入a,b,c分别为1,2,0.3,则输出的结果为(D)
10
A.1.125 B.1.25 C.1.3125 D.1.375
【解析】模拟程序的运行,可得a=1,b=2,c=0.3
执行循环体,m=,不满足条件f(m)=0,
满足条件f(a)f(m)<0,b=1.5,不满足条件|a-b|<c,m=1.25,不满足条件f(m)=0,不满足条件f(a)f(m)<0,a=1.25,满足条件|a-b|<c,
退出循环,输出的值为1.375.故选D.
11.设等差数列{an}的前n项和为Sn,已知(a8-1)3+2 018(a8-1)=1,(a2 011-1)3+2 018(a2 011-1)=-1,则下列结论正确的是(A)
A.S2 018=2 018,a2 011a8
C.S2 018=-2 018,a2 011≤a8 D.S2 018=-2 018,a2 011≥a8
【解析】设f(x)=x3+2 018x,则由f(-x)=-f(x)知函数f(x)是奇函数.由f′(x)=3x2+2 018>0知函数f(x)=x3+2 018x在R上单调递增.因为(a8-1)3+2 018(a8-1)=1,(a2 011-1)3+2 018(a2 011-1)=-1,所以f(a8-1)=1,f(a2 011-1)=-1,得a8-1=-(a2 011-1),即a8+a2 011=2,且a2 0110时,xf′(x)-f(x)<0,则使得f(x)<0成立的x的取值范围是
A.(-∞,-1)∪(0,1) B.(-1,0)∪(1,+∞)
C.(-∞,-1)∪(-1,0) D.(0,1)∪(1,+∞)
【解析】设g(x)=(x≠0),则g′(x)=.
当x>0时,xf′(x)-f(x)<0,∴g′(x)<0,∴g(x)在(0,+∞)上为减函数,
且g(1)=f(1)=-f(-1)=0.
∵f(x)为奇函数,∴g(x)为偶函数,∴g(x)的图象的示意图如右图所示.
当x>0时,由f(x)<0,得g(x)<0,由图知x>1,
10
当x<0时,由f(x)<0,得g(x)>0,由图知-10).
(1)当m=3时,若B=,求sin (A-C)的值;
(2)当m=2时,若c=2,求△ABC面积最大值.
【解析】(1)∵a+b=c,∴sin A+sin B=sin C,
∴sin A+=sin=,4分
化简得sin A+cos A=,∴sin=,
10
∴A+=,即A=,∴C=,
∴sin (A-C)=sin =.6分
(2)∵c=2,∴a+b=2,∴b=2-a,
∴S△ABC=absin C≤ab,8分
∴S△ABC≤ab=a(2-a)=-a2+a,10分
∴当a=时,-a2+a取最大值1,
此时a=b=,c=2满足C=,∴△ABC面积最大值为1.12分
18.(本题满分12分)
如图,四棱锥P-ABCD中,AP⊥平面PCD,AD∥BC,AB=BC=AD,E、F分别为线段AD、PC的中点.
(1)求证:AP∥平面BEF;
(2)设∠PDA=30°,∠BAD=60°,求直线BF与平面PAC所成的角的大小.
【解析】(1)证明:设AC∩BE=O,连接OF、EC.
∵E为AD的中点,AB=BC=AD,AD∥BC,
∴AE∥BC,AE=AB=BC,
∴四边形ABCE为菱形.2分
∴O为AC的中点.3分
又F为PC的中点,在△PAC中,可得AP∥OF.4分
又OF平面BEF,AP平面BEF.5分
∴AP∥平面BEF.6分
(2)由题意知ED∥BC,ED=BC.
∴四边形BCDE为平行四边形,∴BE∥CD.
又AP⊥平面PCD,∴AP⊥CD,∴AP⊥BE.
∵四边形ABCE为菱形,∴BE⊥AC.
又AP∩AC=A,AP、AC平面PAC,∴BE⊥平面PAC.
∴直线BF与平面PAC所成的角为∠BFO.8分
不妨设AP=2,∵∠PDA=30°,∴AE=AD=2,
又∵四边形ABCE为菱形,∠BAD=60°,∴OB=1,
10
∵Rt△BOF中,OF=AP=1,OB=1,∴∠BFO=45°.11分
故直线BF与平面PAC所成的角的大小为45°.12分
19.(本小题满分12分)
已知数列{an}中,Sn为其前n项和,且a1≠a2,当n∈N+时,恒有Sn=pnan(p为常数).
(1)求常数p的值;
(2)当a2=2时,求数列{an}的通项公式;
(3)在(2)的条件下,设bn=,数列{bn}的前n项和为Tn,求证:Tn<.
【解析】(1)当n=1时,a1=S1,∴a1=pa1,p=1或a1=0,
当p=1时,Sn=nan则有S2=2a2a1+a2=2a2a1=a2与已知矛盾,
∴p≠1,只有a1=0.2分
当n=2时,由S2=2pa2a1+a2=2pa2,∵a1=0又a1≠a2,∴a2≠0,
∴p=.4分
(2)∵a2=2,Sn=nan,当n≥2时,an=Sn-Sn-1=an-an-1,6分
(n-2)an=(n-1)an-1=,
∴=an=2n-2.8分
当n=1时,a1=2×1-2=0也适合,∴an=2n-2.9分
(3)bn==<=-.10分
当n=1,2时,显然成立,当n≥3时有
∴Tn<1+++…+=-<.12分
20.(本题满分12分)
已知椭圆C:+=1(a>b>0)的左、右焦点分别为F1、F2,设点F1、F2与椭圆短轴的一个端点构成斜边长为4的直角三角形.
(1)求椭圆C的标准方程;
(2)设A、B、P为椭圆C上三点,满足=+,记线段AB中点Q的轨迹为E,若直线l:y=x+1与轨迹E交于M、N两点,求|MN|.
【解析】(1)由已知得2c=4,b=2,故c=2,a=2.
∴椭圆C的标准方程为+=1.4分
(2)设A(x1,y1),B(x2,y2),
∵=+,∴=,
∴点P坐标为.5分
∵点P在椭圆C上,
∴+=1,
∴++=1,
即++=1,即+=0.6分
10
令线段AB的中点坐标为Q(x,y),则7分
∵A、B在椭圆C上,∴8分
+=2,
∴+=2.
∵+=0,
∴+=2,
即Q点的轨迹E的方程为+=1.9分
联立得3x2+4x-2=0.
设M(x3,y3)、N(x4,y4),
则x3+x4=-,x3·x4=-.10分
故|MN|=|x3-x4|==.12分
第(2)问也可以用椭圆的参数方程解决,且可参考上述解答酌情给分.
21.(本题满分12分)
已知函数f(x)=ex+e-x,g(x)=2x+ax3,a为实常数.
(1)求g(x)的单调区间;
(2)当a=-1时,证明:x0∈(0,1),使得y=f(x)和y=g(x)的图象在x=x0处的切线互相平行.
【解析】(1)g′(x)=3ax2+2,1分
当a≥0时,g′(x)>0故g(x)的单调增区间为(-∞,+∞).3分
当a<0时,令g′(x)≥0得-≤x≤,g(x)的单调增区间为,
g(x)的单调减区间为,.5分
(2)当a=-1时,f′(x)=ex-e-x,g′(x)=2-3x2,
x0∈(0,1),使得y=f(x)和y=g(x)的图象在x=x0处的切线互相平行.
即x0∈(0,1)使得f′(x0)=g′(x0),且f(x0)≠g(x0),6分
令h(x)=f′(x)-g′(x)=ex-e-x-2+3x2,
h(0)=-2<0,h(1)=e--2+3>0,
∴x0∈(0,1)使得f′(x0)=g′(x0).7分
∵当x∈时g′(x)>0,当x∈(,1)时g′(x)<0,
10
∴所以g(x)在区间(0,1)的最大值为g,g=<2.9分
而f(x)=ex+e-x≥2=2,10分
∴x∈(0,1)时f(x)>g(x)恒成立,∴f(x0)≠g(x0).
从而当a=-1时,x0∈(0,1),使得y=f(x)和y=g(x)的图象在x=x0处的切线互相平行.
12分
请考生在第22、23题中任选一题做答,如果多做,则按所做的第一题计分,做答时请写清题号.
22.(本小题满分10分)选修4-4:极坐标与参数方程
在直角坐标系xOy中,曲线M的参数方程为(α为参数),若以直角坐标系的原点O为极点,x轴的正半轴位极轴建立极坐标系,曲线N的极坐标方程ρsin=t(t为参数).
(1)求曲线M和N的直角坐标方程;
(2)若曲线N和曲线M有公共点,求t的取值范围.
【解析】(1)由x=cos α+sin α=2sin得x∈[-2,2],
又∵x2=(cos α+sin α)2=2cos 2α+2sin αcos α+1,
所以曲线M的普通方程为y=x2-1,x∈[-2,2].
由ρsin=t得ρsin θ+ρcos θ=t,
即ρsin θ+ρcos θ=t,所以曲线N的直角坐标方程为x+y=t.4分
(2)若曲线M、N有公共点,则当曲线N过点(2,3)时满足要求,此时t=5,并且向左下方平行移动直到相切之前总有公共点,相切时仍然只有一个公共点,
联立得x2+x-t-1=0,Δ=1+4(1+t)=0t=-.
综上所述,t的取值范围是.10分
23.(本小题满分10分)选修4-5:不等式选讲
已知函数f(x)=.
(1)解不等式f(x)<4-;
(2)已知m+n=1(m,n>0),若-f(x)≤+(a>0)恒成立,求实数a的取值范围.
【解析】(1)不等式f(x)<4-即为<4-.
当x<-时,即-3x-2-x+1<4-1时,即3x+2+x-1<4无解.
综上所述,原不等式的解集为.5分
(2)+=(m+n)=1+1++≥4,
10
令g(x)=-f(x)=-=
所以当x=-时,g(x)max=+a,要使不等式恒成立,只需g(x)max=+a≤40
查看更多