2012高考试题分类汇编：选考内容

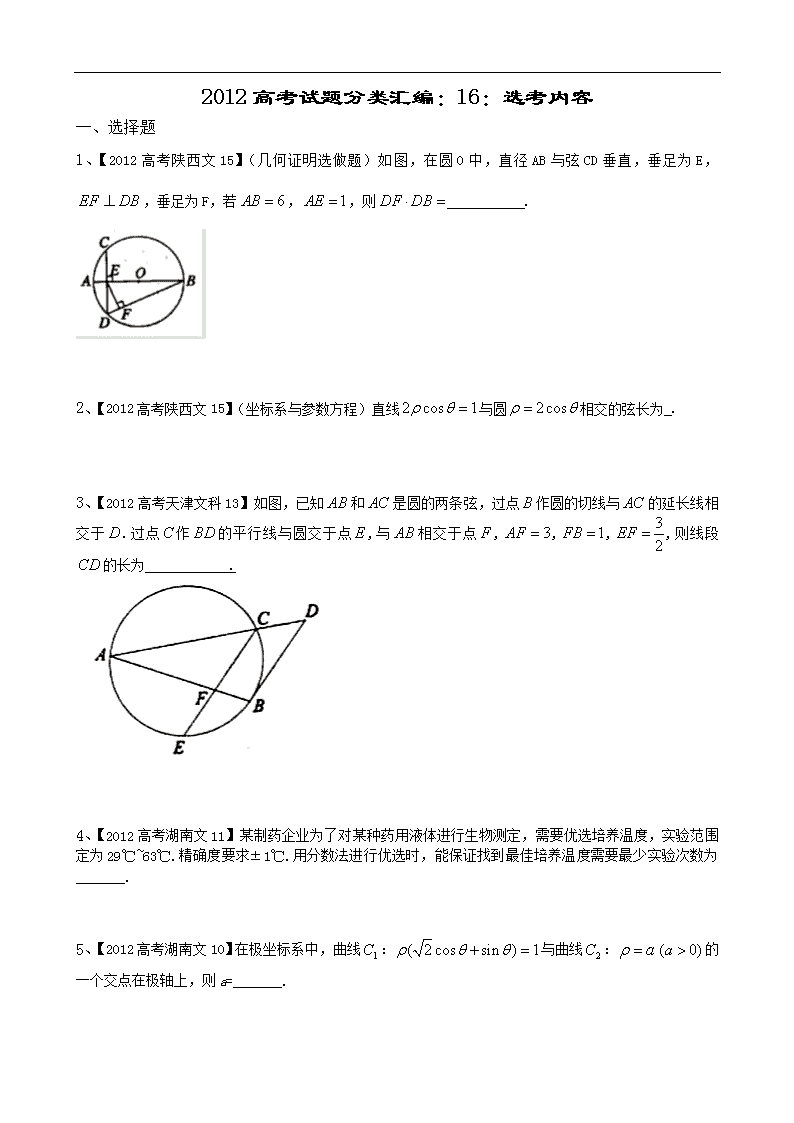
2012高考试题分类汇编：选考内容

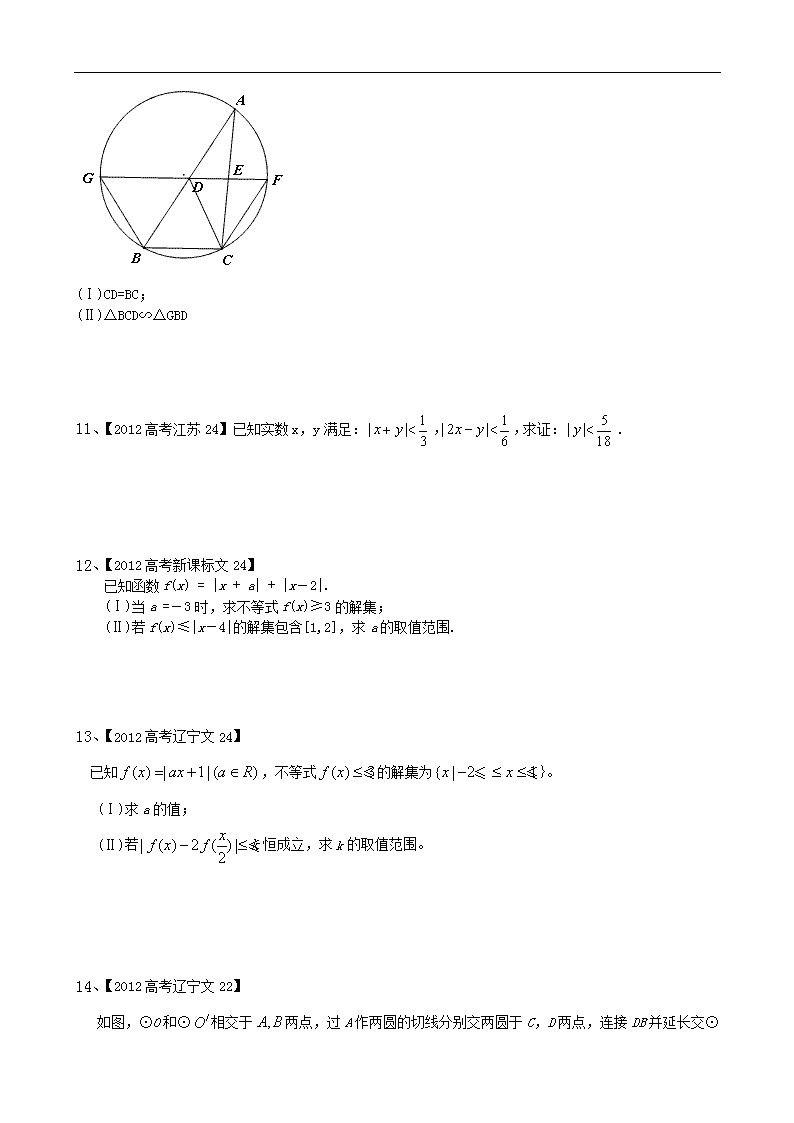
‎2012高考试题分类汇编：16：选考内容 一、选择题 ‎1、【2012高考陕西文15】（几何证明选做题）如图，在圆O中，直径AB与弦CD垂直，垂足为E，，垂足为F，若，，则 . ‎ ‎2、【2012高考陕西文15】（坐标系与参数方程）直线与圆相交的弦长为 .‎ ‎3、【2012高考天津文科13】如图，已知和是圆的两条弦，过点作圆的切线与的延长线相交于.过点作的平行线与圆交于点,与相交于点,,,,则线段的长为 .‎ ‎4、【2012高考湖南文11】某制药企业为了对某种药用液体进行生物测定，需要优选培养温度，实验范围定为‎29℃‎~‎63℃‎.精确度要求±‎1℃‎.用分数法进行优选时，能保证找到最佳培养温度需要最少实验次数为_______.‎ ‎5、【2012高考湖南文10】在极坐标系中，曲线：与曲线：的一个交点在极轴上，则a=_______.‎ ‎6、【2012高考广东文14】（坐标系与参数方程选做题）在平面直角坐标系中，曲线和的参数方程分别为（为参数，）和（为参数），则曲线和的交点坐标为 .‎ ‎7、 【2012高考广东文15】（几何证明选讲选做题）如图3所示，直线与圆相切于点，‎ 是弦上的点，. 若，，则 ‎ .‎ ‎8、【2012高考陕西文15】（不等式选做题）若存在实数使成立，则实数的取值范围是 .‎ 二、解答题 ‎9、【2012高考新课标文23】坐标系与参数方程 ‎ 已知曲线C1的参数方程是 (φ为参数)，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C2的极坐标方程是ρ=2.正方形ABCD的顶点都在C2上，且A、B、C、D以逆时针次序排列，点A的极坐标为(2，)‎ ‎(Ⅰ)求点A、B、C、D 的直角坐标；‎ ‎(Ⅱ)设P为C1上任意一点，求|PA| 2+ |PB|2 + |PC| 2+ |PD|2的取值范围.‎ ‎10、【2012高考新课标文22】如图，D，E分别为△ABC边AB，AC的中点，直线DE交△ABC的外接圆于F，G两点，若CF//AB，证明：‎ ‎(Ⅰ)CD=BC；‎ ‎(Ⅱ)△BCD∽△GBD ‎11、【2012高考江苏24】已知实数x，y满足：求证：．‎ ‎12、【2012高考新课标文24】‎ ‎ 已知函数f(x) = |x + a| + |x－2|.‎ ‎(Ⅰ)当a =－3时，求不等式f(x)≥3的解集；‎ ‎(Ⅱ)若f(x)≤|x－4|的解集包含[1,2]，求a的取值范围.‎ ‎13、【2012高考辽宁文24】‎ ‎ 已知，不等式的解集为｝。‎ ‎ (Ⅰ)求a的值；‎ ‎ (Ⅱ)若恒成立，求k的取值范围。‎ ‎14、【2012高考辽宁文22】‎ ‎ 如图，⊙O和⊙相交于两点，过A作两圆的切线分别交两圆于C，D两点，连接DB并延长交⊙‎ O于点E。证明 ‎ (Ⅰ)；‎ ‎ (Ⅱ) 。‎ ‎15、【2012高考辽宁文23】‎ ‎ 在直角坐标中，圆，圆。‎ ‎ (Ⅰ)在以O为极点，x轴正半轴为极轴的极坐标系中，分别写出圆的极坐标方程，并求出圆的交点坐标(用极坐标表示)；‎ ‎ (Ⅱ)求圆的公共弦的参数方程。‎ ‎16、【2012高考辽宁文24】‎ ‎ 已知，不等式的解集为｝。‎ ‎ (Ⅰ)求a的值；‎ ‎ (Ⅱ)若恒成立，求k的取值范围。‎ ‎17、【2012高考江苏21】如图，是圆的直径，为圆上位于异侧的两点，连结并延长至点，使，连结．‎ 求证：．‎ ‎18、【2012高考江苏22】已知矩阵的逆矩阵，求矩阵的特征值． ‎ ‎19、【2012高考江苏23】[选修4 - 4：坐标系与参数方程] （10分）在极坐标中，已知圆经过点，圆心为直线与极轴的交点，求圆的极坐标方程．‎ ‎20、【2012高考辽宁文24】‎ ‎ 已知，不等式的解集为｝。‎ ‎ (Ⅰ)求a的值；‎ ‎ (Ⅱ)若恒成立，求k的取值范围。‎ 以下是答案 一、选择题 ‎1、5【解析】.连接AD，则∽，,‎ ‎, 又∽,,即.‎ ‎2、 ‎ ‎ ‎ ‎【解析】直线与圆的普通方程为，圆心到直线的距离为，所以弦长为.‎ ‎3、 ‎ ‎【解析】如图连结BC，BE，则∠1=∠2，∠2=∠A ‎，又∠B=∠B，∽，,代入数值得BC=2，AC=4，又由平行线等分线段定理得,解得CD=.‎ ‎4、 ７‎ ‎【解析】用分数法计算知要最少实验次数为7.‎ ‎【点评】本题考查优选法中的分数法，考查基本运算能力.‎ ‎5、 ‎ ‎【解析】曲线的直角坐标方程是，曲线的普通方程是直角坐标方程 ‎，因为曲线C1：与曲线C2：的一个交点在极轴上，所以与轴交点横坐标与值相等，由，知＝.‎ ‎【点评】本题考查直线的极坐标方程、圆的极坐标方程，直线与圆的位置关系，考查转化的思想、方程的思想，考查运算能力；题型年年有，难度适中.把曲线与曲线的极坐标方程都转化为直角坐标方程，求出与轴交点，即得.‎ ‎6、 ‎ ‎【解析】曲线的方程为（），曲线的方程为， 由或（舍去），则曲线和的交点坐标为.‎ ‎7、 ‎ ‎【解析】由弦切角定理得，则△∽△，‎ ‎，则，即.‎ ‎8、.‎ ‎ 【解析】不等式可以表示数轴上的点到点和点1的距离之和小于等于3，因为数轴上的点到点和点1的距离之和最小时即是在点和点1之间时，此时距离和为，要使不等式有解，则，解得.‎ 二、解答题 ‎9、‎ ‎10、 ‎ ‎11、 证明：∵，‎ ‎ 由题设∴。∴。 ‎ ‎【考点】绝对值不等式的基本知识。‎ ‎【解析】根据绝对值不等式的性质求证。‎ ‎12、‎ ‎13、 ‎ ‎【解析】本题主要考查分段函数、不等式的基本性质、绝对值不等式及其运用，考查分类讨论思想在解题中的灵活运用，第(Ⅰ)问，要真对的取值情况进行讨论，第(Ⅱ)问要真对的正负进行讨论从而用分段函数表示，进而求出k的取值范围。本题属于中档题，难度适中．平时复习中，要切实注意绝对值不等式的性质与其灵活运用。‎ ‎14、 ‎ ‎【解析】本题主要考查圆的切线的性质、三角形相似的判断与性质，考查推理论证能力和数形结合思想，重在考查对平面几何基础知识、基本方法的掌握，难度较小。‎ ‎15、‎ ‎【解析】本题主要考查点的极坐标表示、圆的极坐标方程、参数方程的表示及参数方程与一般方程的转换、解方程组的知识，难度较小。本题要注意圆的圆心为半径为，圆的圆心为半径为，从而写出它们的极坐标方程；对于两圆的公共弦，可以先求出其代数形式，然后化成参数形式，也可以直接根据直线的参数形式写出。‎ ‎16、‎ ‎【解析】本题主要考查分段函数、不等式的基本性质、绝对值不等式及其运用，考查分类讨论思想在解题中的灵活运用，第(Ⅰ)问，要真对的取值情况进行讨论，第(Ⅱ)问要真对的正负进行讨论从而用分段函数表示，进而求出k的取值范围。本题属于中档题，难度适中．平时复习中，要切实注意绝对值不等式的性质与其灵活运用。‎ ‎17、证明：连接。‎ ‎ ∵是圆的直径，∴（直径所对的圆周角是直角）。‎ ‎ ∴（垂直的定义）。‎ ‎ 又∵，∴是线段的中垂线（线段的中垂线定义）。‎ ‎ ∴（线段中垂线上的点到线段两端的距离相等）。‎ ‎ ∴（等腰三角形等边对等角的性质）。‎ ‎ 又∵为圆上位于异侧的两点，‎ ‎ ∴（同弧所对圆周角相等）。‎ ‎ ∴（等量代换）。‎ ‎【考点】圆周角定理，线段垂直平分线的判定和性质，等腰三角形的性质。‎ ‎【解析】要证，就得找一个中间量代换，一方面考虑到是同弧所对圆周角，相等；另一方面由是圆的直径和可知是线段的中垂线，从而根据线段中垂线上的点到线段两端的距离相等和等腰三角形等边对等角的性质得到。从而得证。 本题还可连接，利用三角形中位线来求证。‎ ‎18、解：∵，∴。‎ ‎ ∵，∴。‎ ‎ ∴矩阵的特征多项式为。‎ ‎ 令，解得矩阵的特征值。‎ ‎【考点】矩阵的运算，矩阵的特征值。‎ ‎【解析】由矩阵的逆矩阵，根据定义可求出矩阵，从而求出矩阵的特征值。‎ ‎19、 解：∵圆圆心为直线与极轴的交点，‎ ‎∴在中令，得。‎ ‎ ∴圆的圆心坐标为（1，0）。‎ ‎ ∵圆经过点，∴圆的半径为。‎ ‎ ∴圆经过极点。∴圆的极坐标方程为。‎ ‎【考点】直线和圆的极坐标方程。‎ ‎【解析】根据圆圆心为直线与极轴的交点求出的圆心坐标；根据圆经过点求出圆的半径。从而得到圆的极坐标方程。‎ ‎20、‎ ‎【解析】本题主要考查分段函数、不等式的基本性质、绝对值不等式及其运用，考查分类讨论思想在解题中的灵活运用，第(Ⅰ)问，要真对的取值情况进行讨论，第(Ⅱ)问要真对的正负进行讨论从而用分段函数表示，进而求出k的取值范围。本题属于中档.题，难度适中．平时复习中，要切实注意绝对值不等式的性质与其灵活运用。‎