数学卷·2017届河北省定州中学高三下学期周练（2017

数学卷·2017届河北省定州中学高三下学期周练（2017

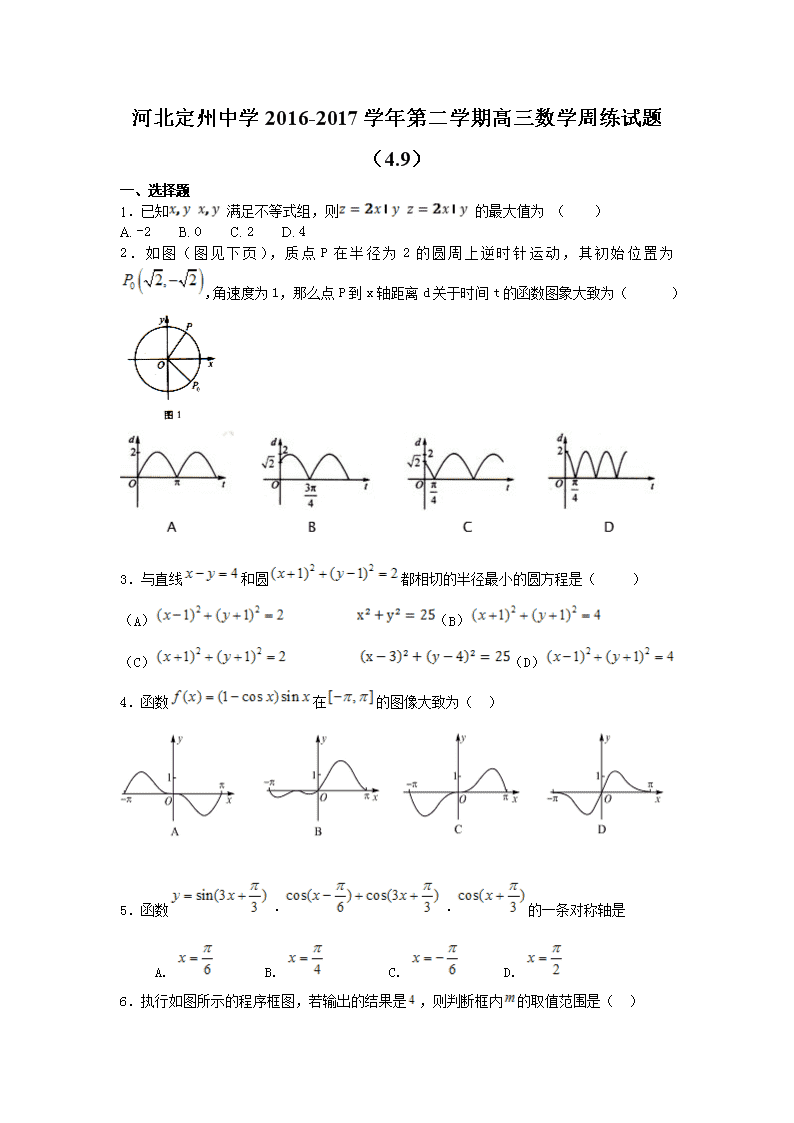
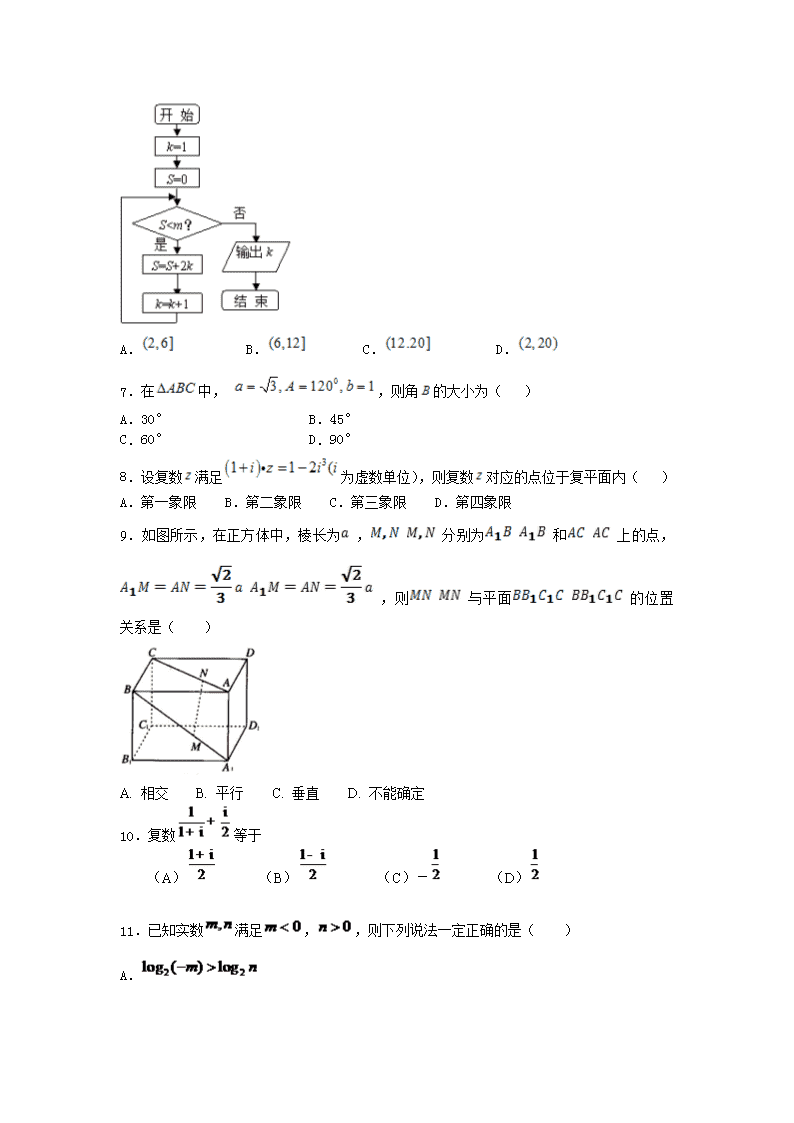
河北定州中学2016-2017学年第二学期高三数学周练试题（4.9）‎ 一、选择题 ‎1．已知满足不等式组，则的最大值为 （ ）‎ A. -2 B. 0 C. 2 D. 4‎ ‎2．如图（图见下页），质点P在半径为2的圆周上逆时针运动，其初始位置为,角速度为1，那么点P到x轴距离d关于时间t的函数图象大致为（ ）‎ ‎ ‎ ‎ ‎ ‎3．与直线和圆都相切的半径最小的圆方程是（ ）‎ ‎（A） （B） ‎ ‎（C） （D）‎ ‎4．函数在的图像大致为（ ）‎ ‎ ‎ ‎ ‎ ‎5．函数··的一条对称轴是 ‎ A. B. C. D. ‎ ‎6．执行如图所示的程序框图，若输出的结果是，则判断框内的取值范围是（ ）‎ ‎ ‎ A． B． C． D．‎ ‎7．在中， ，则角的大小为（ ）‎ A．30° B．45° ‎ C．60° D．90°‎ ‎8．设复数满足为虚数单位），则复数对应的点位于复平面内（ ）‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 ‎ ‎9．如图所示，在正方体中，棱长为，分别为和上的点，，则与平面的位置关系是（ ）‎ ‎ ‎ A. 相交 B. 平行 C. 垂直 D. 不能确定 ‎10．复数等于 ‎ ‎ （A） （B） （C）－ （D）‎ ‎ ‎ ‎11．已知实数满足，，则下列说法一定正确的是（ ）‎ A． ‎ B． ‎ C． ‎ D．‎ ‎12．长方体中，，、与底面所成的角分别为、，则长方体的外接球的体积为（ ）‎ A. B. C. D.‎ ‎ ‎ ‎ ‎ 二、填空题 ‎13．（2015秋•海口校级期中）过点（2，3）且在x轴上的截距为3的直线方程是 ．‎ ‎14．若(n为正偶数)的展开式中第5项的二项式系数最大，则第5项是 ．‎ ‎15．已知=（cosα，1，sinα），=（sinα，1，cosα），则向量+与﹣的夹角是 ．‎ ‎16．已知为正数，且直线与直线互相垂直，则的最小值为________．‎ ‎ ‎ 三、解答题 ‎17．已知二次函数+的图象通过原点，对称轴为，是的导函数，且 .‎ ‎（I）求的表达式；‎ ‎（II）若数列满足，且，求数列的通项公式；‎ ‎（III）若，，是否存在自然数M,使得当时 恒成立?若存在,求出最小的M;若不存在,说明理由.‎ ‎18．己知函数 ‎（1）求函数的最小正周期。‎ ‎（2）记△ABC的内角A、B、C的对边长分别为a、b、c，若，、b=1、c=，求a的值．‎ ‎19．据统计，2016年“双十”天猫总成交金额突破1207亿元．某购物网站为优化营销策略，对11月11日当天在该网站进行网购消费且消费金额不超过1000元的1000名网购者（其中有女性800名，男性200名）进行抽样分析．采用根据性别分层抽样的方法从这1000名网购者中抽取100名进行分析，得到下表：（消费金额单位：元）‎ 女性消费情况：‎ 消费金额 人数 ‎5‎ ‎10‎ ‎15‎ ‎47‎ ‎ ‎ 男性消费情况：‎ 消费金额 人数 ‎2‎ ‎3‎ ‎10‎ ‎2‎ ‎ ‎ ‎（1）计算，的值；在抽出的100名且消费金额在（单位：元）的网购者中随机选出两名发放网购红包，求选出的两名网购者恰好是一男一女的概率；‎ ‎（2）若消费金额不低于600元的网购者为“网购达人”，低于600元的网购者为“非网购达人”，根据以上统计数据填写列联表，并回答能否在犯错误的概率不超过0.010的前提下认为“是否为‘网购达人’与性别有关？”‎ 女性 男性 总计 网购达人 非网购达人 总计 ‎ ‎ 附：‎ ‎0.10‎ ‎0.05‎ ‎0.025‎ ‎0.010‎ ‎2.706‎ ‎3.841‎ ‎5.024‎ ‎6.635‎ ‎（其中）‎ 参考答案 ‎1．C ‎【解析】不等式组的可行域为三角形 其中 令,则的最大值，即为在轴截距相反数的最大值，‎ 其直线过点时值最大，其值为.‎ 的最大值为故本题正确答案是 ‎ ‎2．C ‎【解析】‎ 试题分析：由题意可知，当时，质点到轴的距离为，于是可排除选项，因为角速度为，所以，从而可得质点的轨迹方程为，当时，质点运动到轴的正半轴，此时质点到轴的距离为，所以选C.‎ 考点：周期函数.‎ ‎3．A ‎【解析】‎ 试题分析：由题意可知圆的圆心坐标为（-1,1），半径为 所以过圆心（-1,1）与直线x-y+4=0垂直的直线方程为x+y=0，所求的圆的圆心在此直线上，‎ 又圆心（-1,1）到直线x-y+4=0的距离为 ‎ 则所求圆的半径为，设所求圆的圆心为（a,b），则 且a+b=0，‎ 解得a=1,b=-1，所以所求圆的方程为 考点：本题考查求圆的方程以及直线与圆的位置关系的运用 ‎ 点评：解决本题的关键是数形结合找到圆心的位置 ‎4．C ‎【解析】‎ 试题分析：因为，故排除A；因为，所以函数为奇函数，故排除B；因为，分别作出与的图象，可知极值点在上，故选C．‎ 考点：1、函数的图象；2、函数的奇偶性；3、利用导数研究函数的单调性．‎ ‎5．D ‎【解析】略 ‎ ‎6．B ‎【解析】‎ 试题分析：由程序框图知第一次运行第一次运行S=0+2，k=2；‎ 第二次运行S=0+2+4，k=3；‎ 第三次运行S=0+2+4+6，k=4；‎ ‎∵输出k=4，∴程序运行了3次，此时S=0+2+4+6=12，‎ ‎∴条件为S＜12．‎ ‎∴m的取值范围为6＜m≤12‎ 考点：程序框图 ‎7．A ‎【解析】‎ 试题分析：,故选A.‎ 考点：解三角形.‎ ‎8．A ‎【解析】‎ 试题分析：因为，所以，即复数对应的点位于复平面内第一象限，故选A.‎ 考点：1.复数相关的概念；2.复数的运算.‎ ‎9．B ‎【解析】因为，所以分别取上的点，使得，连，因，且，故，所以四边形是平行四边形，则平面 ‎，平面，则平面，应选答案B。‎ ‎10．D ‎【解析】此题考查复数的运算 解：原式=‎ 答案：D.‎ ‎11．B ‎【解析】‎ 试题分析：当时，成立；；当时，成立；，所以选B.‎ 考点：不等式性质 ‎12．A ‎【解析】‎ 试题分析：∵长方体中，AB=1，与底面ABCD所成的角分别为45°、60°，‎ ‎∴，∵长方体ABCD-A1B1C1D1的各顶点都在同一球面上，∴球的一条直径为，可得半径R=，因此，该长方体ABCD-A1B1C1D1的外接球的体积为，故选：A．‎ 考点：球的体积和表面积．‎ ‎13．3x+y﹣9=0‎ ‎【解析】‎ 试题分析：求出直线的斜率，然后求解直线方程．‎ 解：过点（2，3）且在x轴上的截距为3的直线的斜率为：=﹣3．‎ 所求的直线方程为：y﹣3=﹣3（x﹣2），‎ 即：3x+y﹣9=0．‎ 故答案为：3x+y﹣9=0．‎ 考点：直线的截距式方程．‎ ‎14．x6‎ ‎【解析】‎ 试题分析：因为展开式中第5项的二项式系数最大，所以所以的展开式的第5项为 考点：本小题主要考查二项式定理的应用.‎ 点评：注意到二项展开式的通项公式指的是展开式的第k+1项，而不是第k项.‎ ‎15．90°‎ ‎【解析】‎ 试题分析：由题意可得向量的模长相等，进而可得∴（+）×（﹣）==0，可得结论．‎ 解：∵=（cosα，1，sinα），=（sinα，1，cosα），‎ ‎∴||=||=，‎ ‎∴（+）×（﹣）==0‎ ‎∴+与﹣垂直，‎ ‎∴向量+与﹣的夹角为：90°‎ 故答案为：90°‎ 考点：数量积表示两个向量的夹角．‎ ‎16．9‎ ‎【解析】‎ 试题分析： 因为直线与直线互相垂直，‎ 因为n-（n-2）m=0,所以2m+n=mn，‎ 从而有 ‎，‎ 故答案为：9．‎ 考点：1．直线的一般方程；2．直线的垂直关系．‎ ‎17．（Ⅰ）（Ⅱ）略（III）存在M=4，使得当时，恒成立。‎ ‎【解析】I）由已知，可得，，…………… 1分 ‎ ‎∴ 解之得， ‎ ‎ 3分 ‎ ‎（II） ‎ ‎ ‎ ‎ = 7分 ‎ ‎（III）‎ ‎ 8分 ‎ （1）‎ ‎ （2）‎ ‎（1）—（2）得： 10分 ‎=，即 当时， ‎ ‎，使得当时，恒成立 12分 ‎18．（1）；（2）的值为或.‎ ‎【解析】（1）利用两角和差的正余弦公式化简；（2）利用正弦定理.‎ 解：（1） ‎ 所以函数的最小正周期为. ……6分 ‎（2）由，得,即.‎ 又因为，所以.所以，即. ……8分 因为，所以由正弦定理，得. ……9分 又 故或. ……10分 当时，，从而；‎ 当时，，又，从而. ……11分 故的值为或. ……12分 ‎19．（1）（2）能 ‎【解析】‎ 试题分析：（1）根据分层抽样方法求出的值，利用列举法计算基本事件数，求出对应的概率；（2）列出2×2列联表，计算观测值，对照表中数据，判断结论是否成立即可.‎ ‎（1）依题意，女性应抽取80名，男性应抽取20名，‎ 所以，．‎ 设抽出的100名且消费金额在（单位：元）的网购者中有三位女性记为，，；两位男性记为，，从5人中任选2人的基本事件有：，，，，，，，，，共10个．‎ 设“选出的两名网购者恰好是一男一女”为事件，事件包含的基本事件有：‎ ‎，，，，，共6件，∴．‎ ‎（2）列联表如表所示：‎ 女性 男性 总计 网购达人 ‎50‎ ‎5‎ ‎55‎ 非网购达人 ‎30‎ ‎15‎ ‎45‎ 总计 ‎80‎ ‎20‎ ‎100‎ 因为，所以能在犯错误的概率不超过0.010的前提下认为“是否为‘网购达人’”与性别有关．‎ ‎ ‎