高中数学（人教A版）必修4：2-5-1同步试题（含详解）

高中数学（人教A版）必修4：2-5-1同步试题（含详解）

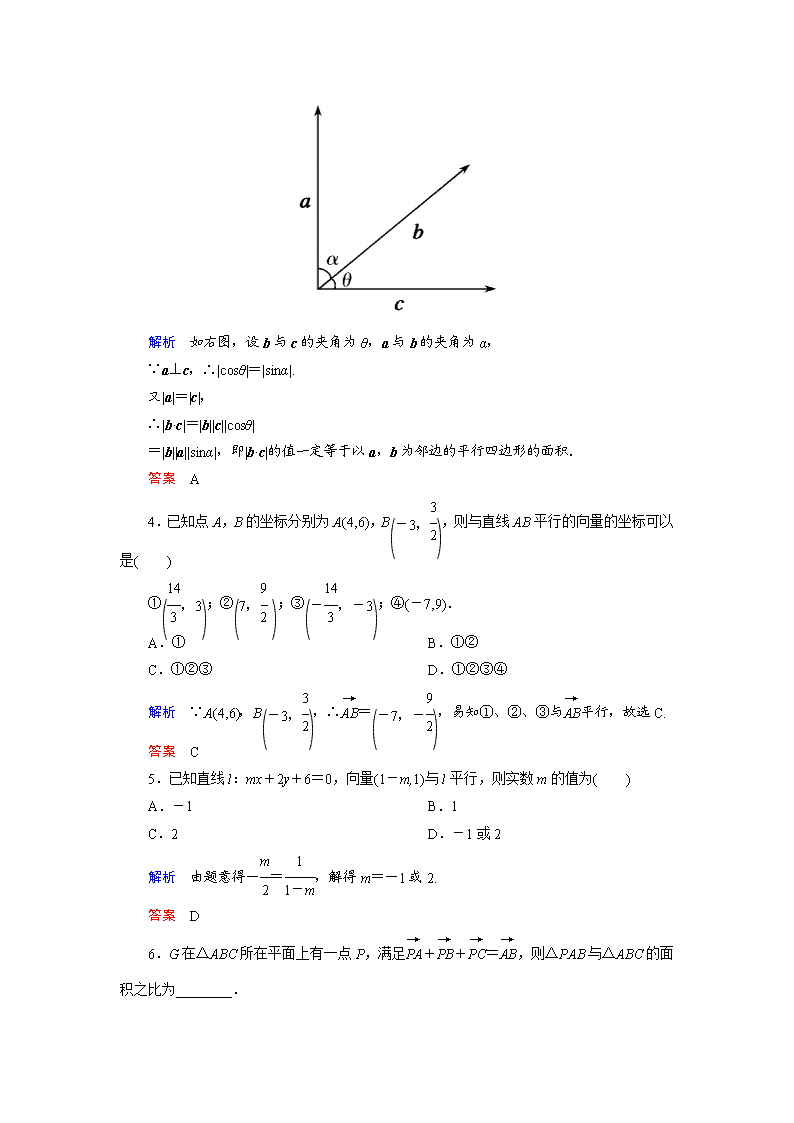
高中数学(人教A版)必修4同步试题 ‎1．在四边形ABCD中，若＋＝0，·＝0，则四边形为(　　)‎ A．平行四边形　　　　　　　 B．矩形 C．等腰梯形 D．菱形 解析　由＋＝0，得＝－＝.‎ ‎∴四边形ABCD为平行四边形．‎ 又·＝0知，对角线互相垂直，故四边形为菱形．‎ 答案　D ‎2．在△ABC中，AB＝AC，D，E分别是AB，AC的中点，则(　　)‎ A.＝ B.与共线 C.＝ D.与共线 解析　由题意知，DE为△ABC的中位线，‎ ‎∴DE∥BC，∴与共线．‎ 答案　D ‎3．设a，b，c为同一平面内具有相同起点的任意三个非零向量，且满足a与b不共线，a⊥c，|a|＝|c|，则|b·c|的值一定等于(　　)‎ A．以a，b为邻边的平行四边形的面积 B．以b，c为邻边的平行四边形的面积 C．以a，b为两边的三角形的面积 D．以b，c为两边的三角形的面积 解析　如右图，设b与c的夹角为θ，a与b的夹角为α，‎ ‎∵a⊥c，∴|cosθ|＝|sinα|.‎ 又|a|＝|c|，‎ ‎∴|b·c|＝|b||c||cosθ|‎ ‎＝|b||a||sinα|，即|b·c|的值一定等于以a，b为邻边的平行四边形的面积．‎ 答案　A ‎4．已知点A，B的坐标分别为A(4,6)，B，则与直线AB平行的向量的坐标可以是(　　)‎ ‎①；②；③；④(－7,9)．‎ A．① B．①②‎ C．①②③ D．①②③④‎ 解析　∵A(4,6)，B，∴＝，易知①、②、③与平行，故选C.‎ 答案　C ‎5．已知直线l：mx＋2y＋6＝0，向量(1－m,1)与l平行，则实数m的值为(　　)‎ A．－1 B．1‎ C．2 D．－1或2‎ 解析　由题意得－＝，解得m＝－1或2.‎ 答案　D ‎6．G在△ABC所在平面上有一点P，满足＋＋＝，则△PAB与△ABC的面积之比为________．‎ 解析　∵＋＋＝，‎ ‎∴＝－－＝＋＋＝2，‎ ‎∴A，P，C三点共线，且点P是靠近点A的线段AC的三等分点，故＝.‎ 答案　 ‎7．如下图，在△ABC中，点O是BC的中点，过点O的直线分别交直线AB，AC于不同的两点M，N，若＝m，＝n，则m＋n的值为________．‎ 解析　如下图，过B作BD∥MN，‎ 易知m＝＝，n＝，‎ ‎∴m＋n＝.∵＝＝1，‎ ‎∴AD＋AC＝2AN.‎ ‎∴m＋n＝2.‎ 答案　2‎ ‎8．利用向量证明：菱形的两条对角线互相垂直．‎ 证明　设菱形ABCD，‎ 则||＝||‎ ·＝(＋)(－)‎ ‎＝()2－()2＝||2－||2＝0，‎ ‎∴⊥，即AC⊥BD.‎ ‎9．已知：AM是△ABC中BC边上的中线，求证：‎ AM2＝(AB2＋AC2)－BM2.‎ 证明　∵M是BC的中点，‎ ‎∴＝(＋)，＝，‎ ‎|AM|2＝(||2＋||2)＋·.‎ ‎∵＝＋，＝＋，‎ ‎∴·＝||2－||2.‎ ‎∴||2＝(||2＋||2)＋(||2－||2)．‎ ‎∴AM2＝(AB2＋AC2)－BM2.‎ ‎10．如图所示，以原点和A(5,2)为两个顶点作等腰直角三角形OAB，∠B＝90°，求点B的坐标．‎ 解　设B(x，y)，则||＝.‎ ‎∵B(x，y)，A(5,2)，‎ ‎∴||＝.‎ 又||＝||，‎ ‎∴＝，‎ 整理，得10x＋4y＝29①‎ ‎∴又＝(x，y)，＝(x－5，y－2)，且⊥.‎ ‎∴·＝0，∴x(x－5)＋y(y－2)＝0，‎ 即x2＋y2－5x－2y＝0，②‎ 由①、②解得或 ‎∴B或.‎ 教师备课资源 ‎1.在△ABC中，若||＝1.5，||＝1.5，||＝1，则|－|的值为(　　)‎ A．0　　　　B．‎1　‎　　　C.　　　　D．2‎ 解析　|－|＝||＝1.‎ 答案　B ‎2．在△ABC中，∠C＝90°，＝(k,1)，＝(2,3)，则k的值是(　　)‎ A. B．－ ‎ C．5 D．－5‎ 解析　＝－＝(2,3)－(k,1)＝(2－k,2)．‎ ‎∵∠C＝90°，∴⊥，∴·＝0.‎ ‎∴(2,3)·(2－k,2)＝0，‎ 即2(2－k)＋6＝0，∴k＝5.‎ 答案　C ‎3．如图，在▱ABCD中，＝(1,2)，＝(－3,2)，则·＝________.‎ 解析　设AC与BD的交点是O，则＝＝，＝＝(，1)，‎ ‎∴＝＋＝(－1,2)．‎ 又＝(1,2)，‎ ‎∴·＝1×(－1)＋2×2＝3.‎ 答案　3‎ ‎4．在▱ABCD中，＝(1,2)，＝(－3,2)，则的坐标为________．‎ 解析　＝＋＝(1,2)＋(－3,2)＝(－2,4)．‎ 答案　(－2,4)‎ ‎5．已知O，N，P在△ABC所在的平面内，且||＝||＝||，＋＋＝0，·＝·＝·，则点O，N，P依次是△ABC的(　　)‎ A．重心　外心　垂心 B．重心　外心　内心 C．外心　重心　垂心 D．外心　重心　内心 ‎(注：三角形的三条高线交于一点，此点为三角形的垂心)‎ 解析　由||＝||＝||知，O为△ABC的外心；‎ 由＋＋＝0知，N为△ABC的重心；‎ ‎∵·＝·，∴·(－)＝0.‎ ‎∴·＝0，∴⊥，同理⊥.‎ ‎∴P是△ABC的垂心．‎ 答案　C