- 2021-06-17 发布 |
- 37.5 KB |
- 8页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
重庆市黔江新华中学校2019-2020学年高一上学期期中考试数学试卷 含答案
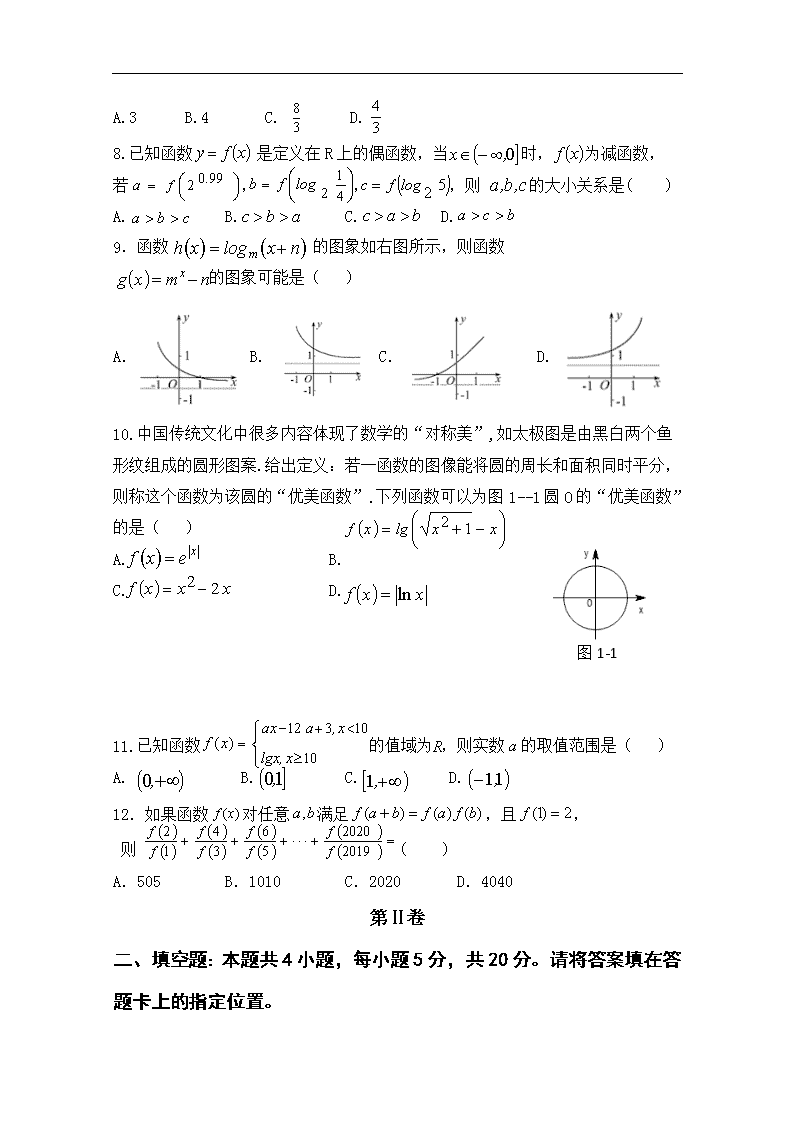
www.ks5u.com 数学试题 (考试时间:120分钟 总分:150分) 注意事项:本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.其中选择题部分用2B铅笔在答题卡相应位置填涂;非选择题部分用0.5mm黑色签字笔在答题卡相应位置书写,在试题卷上作答的一律无效. 第Ⅰ卷 一、选择题:本题共12小题,每小题5分,共60分。每小题给出的四个选项中,只有一个选项是符合题目要求的。 1.设全集 ,集合 , , 则 =( ) A. {1,3,7,8} B. {0,2,4,5,6,9,10} C. {0,5,6,10} D.{2,4,5,9,10} 2.下列函数中,既是偶函数又在 上单调递减的函数是( ) A. B. C. D. 3.德国数学家狄利克雷在数学上做出了名垂史册的重大贡献,函数 是以他名字命名的函数,则 ( ) A.1 B.0 C. D.-1 4.如图,设全集, , ,其Venn图如下,则图中阴影部分表示的集合为( ) N M A. B. C. D. 5.函数 的定义域是( ) A. B. C. D. 6.下列四组函数中,两个函数是同一函数的是( ) A. 与 B. 与 C. 与 D. 与 7.若对于任意非零实数 都有,则 =( ) A.3 B.4 C. D. 8.已知函数 是定义在R上的偶函数,当 时, 为减函数,若 , , ,则 的大小关系是( ) A. B. C. D. 9.函数 的图象如右图所示,则函数 的图象可能是( ) A. B. C. D. 10.中国传统文化中很多内容体现了数学的“对称美”,如太极图是由黑白两个鱼形纹组成的圆形图案.给出定义:若一函数的图像能将圆的周长和面积同时平分,则称这个函数为该圆的“优美函数”.下列函数可以为图1--1圆O的“优美函数”的是( ) A. B. C. D. 图1-1 11.已知函数 的值域为 ,则实数 的取值范围是( ) A. B. C. D. 12.如果函数对任意满足,且, 则 ( ) A.505 B.1010 C.2020 D.4040 第Ⅱ卷 二、填空题:本题共4小题,每小题5分,共20分。请将答案填在答题卡上的指定位置。 13.已知集合 ,集合 .若 ,则实数 =_____. 14.函数 的图像恒过定点 ,且点 在幂函数 的图像上,则 _______. 15.已知 ,若 且 ,则 =____; =_____. 16.关于函数 ,有下列命题:①当 时, 是增函数;当 时, 是减函数;②其图象关于 轴对称;③ 无最大值,也无最小值;④ 在区间 , 上是增函数;⑤ 的最小值是.其中所有正确命题的序号是_________. 三、解答题:本题共6小题,17小题10分,18—22小题每小题12分,共70分。解答题应写出文字说明、证明过程或演算步骤。 17.(本小题满分10分)(1)计算 ; (2)已知 , 求 的值. 18.(本小题满分12分)已知集合A={ |2≤≤8},B={ | }. ... (1)求 ; (2)已知集合C={ |1< < },若 ,求实数 的取值范围. 19.(本小题满分12分)已知 是定义在R上的偶函数,且当 时图象是如图所示的抛物线的一部分. (1)写出函数 的表达式; (2)若函数 ,求 的最小值. 20.(本小题满分12分)已知 对任意实数都有 且当 时,有 . (1)求证: 在R上为增函数; (2)若 ,求满足不等式 的实数 的取值范围. 21.(本小题满分12分)设函数 ,且 , . (1)求 , 的值;(2)若函数 的图象与 的图象恒有两个交点,求 的取值范围. 22.(本小题满分12分)已知函数 ( 且 )是定义在 上的奇函数. (1)求 的值; (2)求函数 的值域; (3)当 时,不等式 恒成立,求实数 的取值范围. 答案 一、 选择题 BCAC DDAB ABBC 二、 填空题 13. 14.49 15.m=4,n=2 16.①③ 三. 解答题 17. 每小题5分 (1) (2) 18.解:(1)A={x|2≤2x≤8}={x|1≤x≤3}…..1分 ..…2分 (CRB)∪A={x|x≤2}∪{x|1≤x≤3}={x|x≤3}…..6 (2)当a≤1时,C=∅,此时C⊆A…8分 当a>1时,C⊆A,则1<a≤3…10分 综上所述,a的取值范围是(﹣∞,3]…..12分 19.当时,设解析式是,代入得,…..2分 即 因为f(x)为偶函数 当x<0时,-x>0 …..5分 所以解析式是…..6分 (2) 对称轴为 (i) 当 …..8分 (ii) 当 …..10分 (iii) 当 …..12分 20.(1)证明:任取 且 则. , , 在R上为增函数. …..6分 (3) ,即, ` .…..8分 , …..10分 又在R上为增函数, ,即 故实数的取值范围为. …..12分 21.解:(1)∵f(1)=lg6,f(2)=lg72,f(x)=lg(ax﹣bx) ∴,….3分 解得∴a=9,b=3;….5分 (2)若函数g(x)=ax的图象与h(x)=bx﹣c的图象恒有两个交点.则方程9x﹣3x +c=0有两个解,…..8分 令t=3x,则t>0,则方程有两个正解;…..10分 故,解得. 所以当时,函数g(x)=ax的图象与h(x)=bx﹣c的图象恒有两个交点.…..12分 22. 解(1)∵是上的奇函数, ∴整理可得a=3.…..2分 (2)由(1)可得, ∴函数在上单调递增,…..4分 又, ∴, ∴. ∴函数的值域为.….7分 (3)当时,. 由题意在恒成立 得 ∴在时恒成立. 令,则有,…..9分 ∵当时函数为增函数, ∴. ∴. 故实数的取值范围为.…..12分查看更多