2018-2019学年甘肃省会宁县第二中学高二上学期第一次月考数学（文）试题（Word版）

2018-2019学年甘肃省会宁县第二中学高二上学期第一次月考数学（文）试题（Word版）

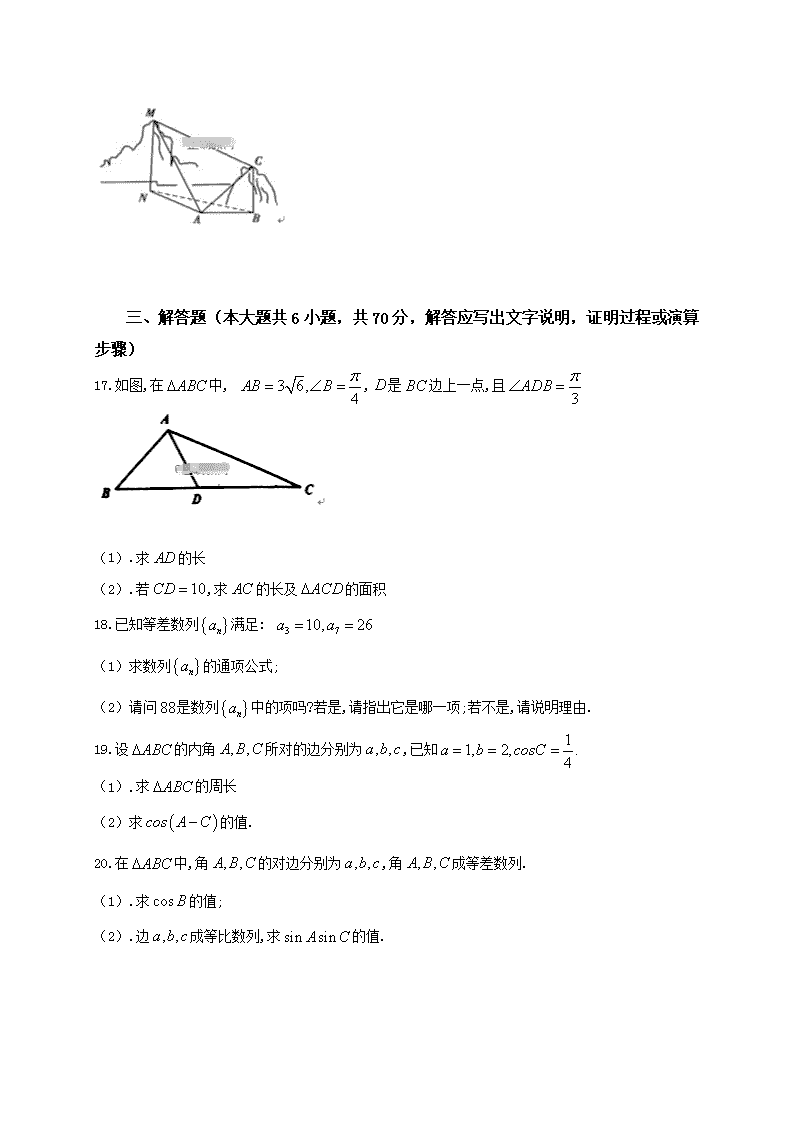
‎2018-2019学年甘肃省会宁县第二中学高二上学期第一次月考数学(文)（人教版）‎ 本试卷分选择题和非选择题两部分。考试结束后，将答题卡交回。试卷满分150分，考试时间120分钟。‎ 注意事项：1．开始答卷前，考生务必将自己的班级、姓名填写清楚。‎ ‎2．将试题答案填在相应的答题卡内，在试卷上作答无效。‎ 一、选择题：本题共12小题，每小题5分。‎ ‎1.在中, ,则等于(   )‎ A.30°       B.45°       C.60°       D.120°‎ ‎2.中, ,则此三角形解的情况是(   )‎ A.一解       B.两解       C.无解       D.无法确定 ‎3.数列的通项公式等于(   )‎ A. B. C. D. ‎ ‎4.数列的通项公式是则这个数列的前项是(   )‎ A.1,4,9      B.2,4,9      C.2,1,4      D.2,6,11‎ ‎5.边长为的三角形中,最大角与最小角之和为(   )‎ A. B. C. D. ‎ ‎6.已知等差数列的前13项之和为39,则等于(   )‎ A.6          B.9          C.12         D.18‎ ‎7.在中,内角的对边分别为,已知, 则为(   )‎ A.直角三角形                 B.等腰三角形 C.等腰直角三角形               D.等边三角形 ‎8.已知中, ,则的取值范围为( )‎ A. B. C. D. ‎ ‎9.在等差数列中, ,则的值为(   )‎ A.5          B.6          C.8          D.10‎ ‎10.在等差数列中,已知,公差,则 (   )‎ A.10         B.12         C.14         D.16‎ ‎11设分别是等差数列的前n项和,若,则( )‎ A.    B.    C.    D.‎ ‎12.已知分别为内角的对边,且成等比数列,且,则 (   )‎ A. B. C. D. ‎ 二、填空题：（本大题共4小题，每题5分，共20分，把答案填在题中横线上）‎ ‎13已知△ABC的面积为,且b=2,c=,则∠A=        .‎ ‎14.根据下列4个图形及相应点的个数的变化规律,试猜测第n个图形中有__________个点 ‎ ‎15.数列中的前项和,则通项公式__________‎ ‎16.如图,为测量山高,选择和另一座山的山顶为测量观测点,从点测得点的仰角,点的仰角以及;从点测得,已知山高,求山高__________.‎ 三、 解答题（本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤）‎ ‎17.如图,在中, ,是边上一点,且 ‎（1）.求的长 ‎（2）.若,求的长及的面积 ‎18.已知等差数列满足: ‎ ‎（1）求数列的通项公式;‎ ‎（2）请问是数列中的项吗?若是,请指出它是哪一项;若不是,请说明理由.‎ ‎19.设的内角所对的边分别为,已知 ‎（1）.求的周长 ‎（2）求的值.‎ ‎20.在中,角的对边分别为,角成等差数列.‎ ‎（1）.求的值;‎ ‎（2）.边成等比数列,求的值.‎ ‎21.等差数列中, ,. （1）.求数列的通项公式; （2）.设,求的值.‎ ‎22.已知函数 ‎（1）.求函数的单调减区间 ‎（2）.已知中,角所对的边分别为,其中,若锐角满足,且,求的值 参考答案 ‎ ‎ 一、选择题 ‎1.答案：C 解析：‎ 所以 ‎2.答案：B 解析：∵∴,又 ‎∴此三角形有两解 ‎3.答案：C ‎4.答案：B ‎5.答案：B 解析：根据三角形角边关系可得,最大角与最小角所对的边的长分别为与, 设长为的边所对的角为,则最大角与最小角的和是, 有余弦定理可得, , 易得,则最大角与最小角的和是,故选B.‎ ‎6.答案：B 解析：由题意，得，所以，解得，所以 ‎7.答案：A 解析：∵,∴,,.‎ 代入,得,∴.∴为直角三角形.故选A.‎ ‎8.答案：A 解析：由正弦定理知,‎ 所以,‎ 由得 ‎9.答案：A 解析：在等差数列中,由,得 ,故选A ‎10.答案：B 解析：‎ 答案： D解析： 根据等差数列的前项和公式知和为:,所以设,所以当时,,所以,所以答案为D.‎ ‎12.答案：C 解析：‎ 二、填空题 答案： ‎ ‎13.60°或120°14.答案：解析：‎ ‎15.答案：‎ ‎16.答案：150‎ 解析：在中, ,在中, ,解得,在中, ,故,即山高为.‎ 三、解答题 ‎17.答案：1.在中,由正弦定理得,得 2.由1知由余弦定理得 ‎∴,‎ 解析：‎ ‎18.答案：1.依题意知 ‎∴ 2.令,即 所以∵‎ 所以不是数列中的项 ‎19.1.因为所以.所以的周长为. 2.因为所以 所以 .‎ 所以 ‎20.答案：1. 由已知,得,∴. 2. 由已知及,根据正弦定理得,‎ ‎∴.‎ 解析：‎ ‎21.答案：1.设等差数列的公差为. 由已知得. 解得, 所以. 2.由1可得. 所以 .‎ 解析：‎ ‎22.答案：1. ‎ 由,得的单调递减区间为 2.由,又∵为锐角,∴‎ 由正弦定理可得,,则,‎ 由余弦定理知,解得 解析：‎