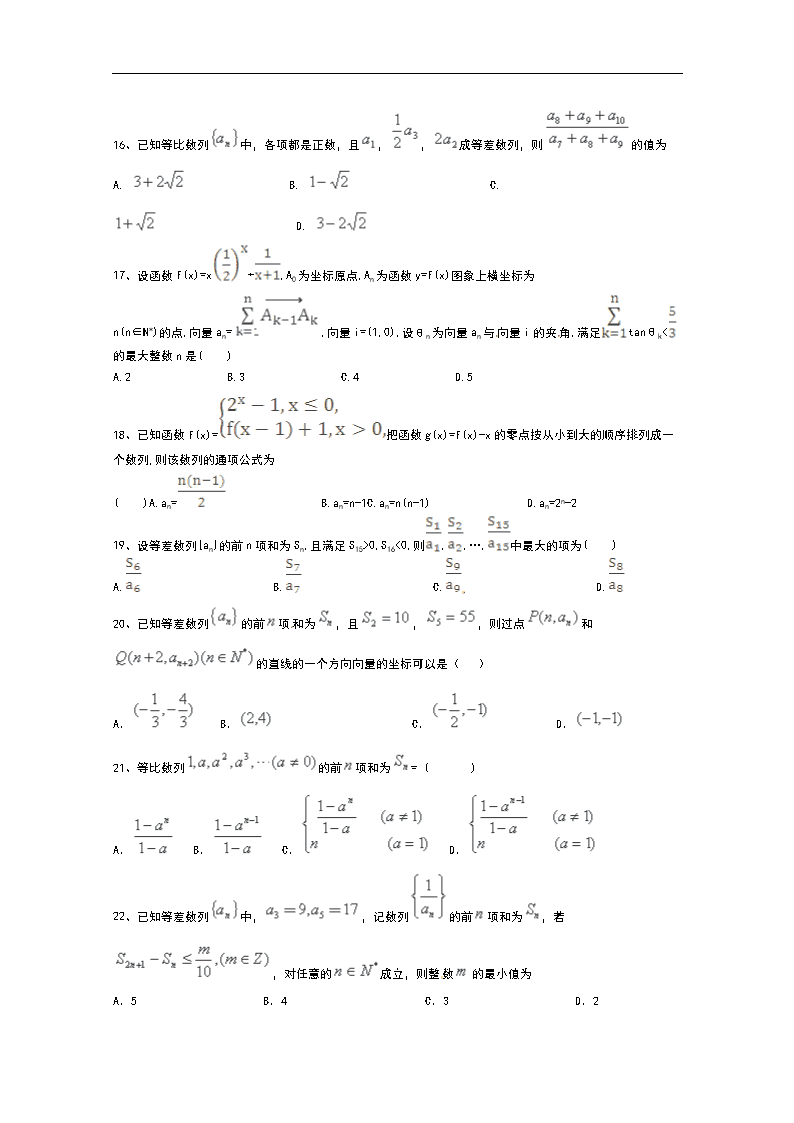2015届高考数学二轮复习专题训练试题:数列(1)
数列(1)
1、已知定义在上的函数、满足,其中且,在有穷数列中任取前项相加,则前项 和大于的概率是( ) A 、 B、 C、 D、
2、已知一次函数的图像经过点和,令,记数列的前项和为,当时,的值等于A . B. C. D.
3、已知数列{an},如果是首项为1,公比为2的等比数列,那么an = ( ) A.2n+1-1 B.2n-1 C.2n-1 D.2n +1
4、 已知,,成等差数列,成等比数列,则的最小值是( )
(A) (B) (C) (D)
5、 在数列{an}中,如果存在非零常数T,使得am+T=am对于任意的非零自然数m均成立,那么就称数列{an}为周期数列,其中T叫数列{an}的周期.已知数列{xn}满足xn+1=|xn-xn-1|(n≥2,n∈N),如果x1=1,x2=a(a∈R,a≠0),当数列{xn}的周期最小时,该数列前2005项的和是( ) A.668 B.669 C.1336 D.1337
6、已知等差数列{an}和等比数列{bn}各项都是正数,且a1=b1,a2n+1=b2n+1,那么一定有 ( )
A.an+1≤bn+1 B.an+1≥bn+1 C.an+1
bn+1
7、 互不相等的三个正数x1、x2、x3成等比数列,且点P1(logax1,logby1)、P2(logax2,logby2)、P3(logax3,logby3)共线(a>0且a≠1,b>0且b≠1),则y1、y2、y3成 ( )
A.等差数列,但不成等比数列 B.等比数列而非等差数列 C.等比数列,也可能成等差数列
D.既不是等比数列,又不是等差数列
8、已知数列{an}的前n项和Sn=a[2-()n-1]-b[2-(n+1)()n-1](n=1,2,…),其中a,b是非零常数,则存在数列{xn}、{yn}使得( )
A.an=xn+yn,其中{xn}为等差数列,{yn}为等比数列B.an=xn+yn,其中{xn}和{yn}都为等差数列
C.an=xn·yn,其中{xn}为等差数列,{yn}为等比数列D.an=xn·yn,其中{xn}和{yn}都为等比数列
9、若{an}是等差数列,首项a1>0,a2003+a2004>0,a2003·a2004<0,则使前n项和Sn>0成立的最大自然数n是 ( )
A.4005 B.4006 C.4007 D.4008
10、已知函数,若数列满足,且是递减数列,则实数的取值范围是( )(A) (B) (C) (D)
11、已知数列{an}的前n项和Sn=2n+1-2,等差数列{bn}中,b2 = a2,面bn+3+bn-1=2bn+4, (n2,nN+), 则bn=
A. 2n+2 B.2n C. n-2 D.2n-2
12、已知数列{an}的通项公式为an=2n+1,令bn=(a1+a2+…+an),则数列{bn}的前10项和T10=( )
A.70 B.75C.80 D.85[来源:学科网]
13、已知数列满足下面说法正确的是
①当时,数列为递减数列;②当时,数列不一定有最大项;
③当时,数列为递减数列;④当为正整数时,数列必有两项相等的最大项.
A. ①② B. ②④ C. ③④ D. ②③
14、 [来源:学科网]
A.12084 B.12090 C.12096 D.12102
15、各项均为正数的数列 的前n项和Sn ,且
A. B. C D.
16、已知等比数列中,各项都是正数,且,,成等差数列,则的值为
A. B. C. D.
17、设函数f(x)=x+,A0为坐标原点,An为函数y=f(x)图象上横坐标为[来源:Z#xx#k.Com]
n(n∈N*)的点,向量an=,向量i=(1,0),设θn为向量an与向量i的夹角,满足tanθk<的最大整数n是( )[来源:学科网ZXXK]
A.2 B.3 C.4 D.5
18、已知函数f(x)=把函数g(x)=f(x)-x的零点按从小到大的顺序排列成一个数列,则该数列的通项公式为( )A.an= B.an=n-1C.an=n(n-1) D.an=2n-2
19、设等差数列{an}的前n项和为Sn,且满足S15>0,S16<0,则,,…,中最大的项为( )
A. B. C. D.
20、已知等差数列的前项和为,且,,则过点和的直线的一个方向向量的坐标可以是( )A. B. C. D.
21、等比数列的前项和为= ( )
A. B. C. D.
22、已知等差数列中,,记数列的前项和为,若,对任意的成立,则整数的最小值为A.5 B.4 C.3 D.2
23、已知两个等差数列和的前项和分别为A和,且,则使得为整数的正整数的个数是( )A.2 B.3 C.4 D.5
24、设等差数列的前项和为且满足则中最大的项为 ( )
25、等差数列的前n项和为,且,则的最小值是
A7 B C8 D
26、已知等比数列的前项和为,若,且满足,则使的的最大值为( )(A)6 (B)7 (C)8 (D)9
27、设为数列的前项和,,其中是常数.则为( )
A. B. C. D.
28、数列的首项为3,为等差数列且.若则,则( )
(A) 0 (B) 3 (C) 8 (D) 11
29、数列前项和为,已知,且对任意正整数,都有,若恒成立则实数的最小值为( )A. B. C. D.2
30、设有无穷数列,且为正整数集的无限子集,,则数列称为数列的一个子列,记为.下面关于子列的三个命题①对任何正整数,必有;
②已知为等差数列,则“为等差数列”是“为等差数列”的充分不必要条件;
③已知为等比数列,则“为等差数列”是“为等比数列”的充分不必要条件.[来源:学§科§网Z§X§X§K]
真命题的个数是A.0 B.1 C..2 D.3
31、已知,把数列的各项排列成如下的三角形状,记表示第行的第个数,则= ( ) A. B. C. D.
32、数列满足并且,则数列的第100项为( )
A. B. C. D.
33、已知数列的前项和,正项等比数列中,,,则( )
A. B. C. D.
34、设等差数列的前项和为,若,则必定有( )
A. ,且 B. ,且 C. ,且 D. ,且
35、设,,,则数列成 ( )
A. 等差数列 B. 等比数列 C. 非等差也非等比数列 D. 既等差也等比数列
36、已知正项等比数列{an},a1=2,又bn=log2an,且数列{bn}的前7项和T7最大,T7≠T6,且T7≠T8,则数列{an}的公比q的取值范围是( )(A)<q< (B)<q<(C)q<或q> (D)q>或q<
37、若数列{an}满足=p(p为正常数,n∈N+),则称{an}为“等方比数列”.甲:数列{an}是等方比数列;乙:数列{an}是等比数列,则( )(A)甲是乙的充分条件但不是必要条件(B)甲是乙的充要条件
(C)甲是乙的必要条件但不是充分条件(D)甲既不是乙的充分条件也不是乙的必要条件
38、在数列中,如果存在常数,使得对于任意正整数均成立,那么就称数列为周期数列,其中叫做数列的周期. 已知周期数列满足,若,当数列的周期为时,则数列的前2015项的和为( )
A.1344 B.1343 C.1342 D. 1341
39、已知数列{an}的通项公式是,其中a、b均为正常数,那么数列{an}的单调性为( )
A.单调递增 B.单调递减 C.不单调 D.与a、b的取值相关
40、已知定义在上的函数满足:
设数列 的前项和为,则的取值范围是A. B. C. D.
1、D 2、A 3、B 4、D 5、D 6、B 7、C 8、C. a1=S1=3a an=Sn-Sn-1=a[2+()n-1]-b[2-(n+1)·()n+1]-a[2+()n-2]+b[2-n()n-2]=(bn-b-a)·()n-1 ∵{()n-1}为等比数列,{bn-a-b}为等差数列. 9、B【正确解答】 B ∵a1>0,a2003+a2004>0,a2003·a2004<0,且{an}为等差数列 ∴{an}表示首项为正数,公差为负数的单调递减等差数列,且a2003是绝对值最小的正数,a2004是绝对值最大的负数(第一个负数),且|a2003|>|a2004|∴在等差数列{an}中,a2003+a2004=a1+a4006>0,S4006=>0 ∴使Sn>0成立的最大自然数n是4006. 10、C 11、B
12、B解析 由已知an=2n+1,得a1=3,a1+a2+…+an==n(n+2),则bn=n+2,T10==75,故选B.
13、C 14、B 15、B16、C 17、B.由已知得An,又an===,tanθn===+,
所以tanθk=+=2--,
验证知n=3符合tanθk<.
18、B.当x≤0时,g(x)=2x-1-x,令g(x)=0,得x=0.当00,得a8>0.由S16==<0,得a9+a8<0,所以a9<0,且d<0.
所以a1>a2>…>a8>0>a9>…>a15,S8>S7>…>S1>0,0>…>>0>,从而最大.选D.
20、A 21、C 22、B23、D 24、C 25、D 26、D 27、B28、B 29、A30、D 31、A 32、D 33、D 34、A 35、A
36、B.∵bn=log2an,而{an}是以a1=2为首项,q为公比的等比数列,∴bn=log2an=log2(a1qn-1)=1+(n-1)log2q.
∴bn+1-bn=log2q.∴{bn}是等差数列,由于前7项之和T7最大,且T7≠T6,所以有解得-<log2q<-,
即<q<.故选B.
37、C.乙⇒甲,但甲 乙,如数列2,2,-2,-2,-2,是等方比数列,但不是等比数列.38、A 39、A 40、B