2021高考数学一轮复习课时作业61几何概型理

2021高考数学一轮复习课时作业61几何概型理

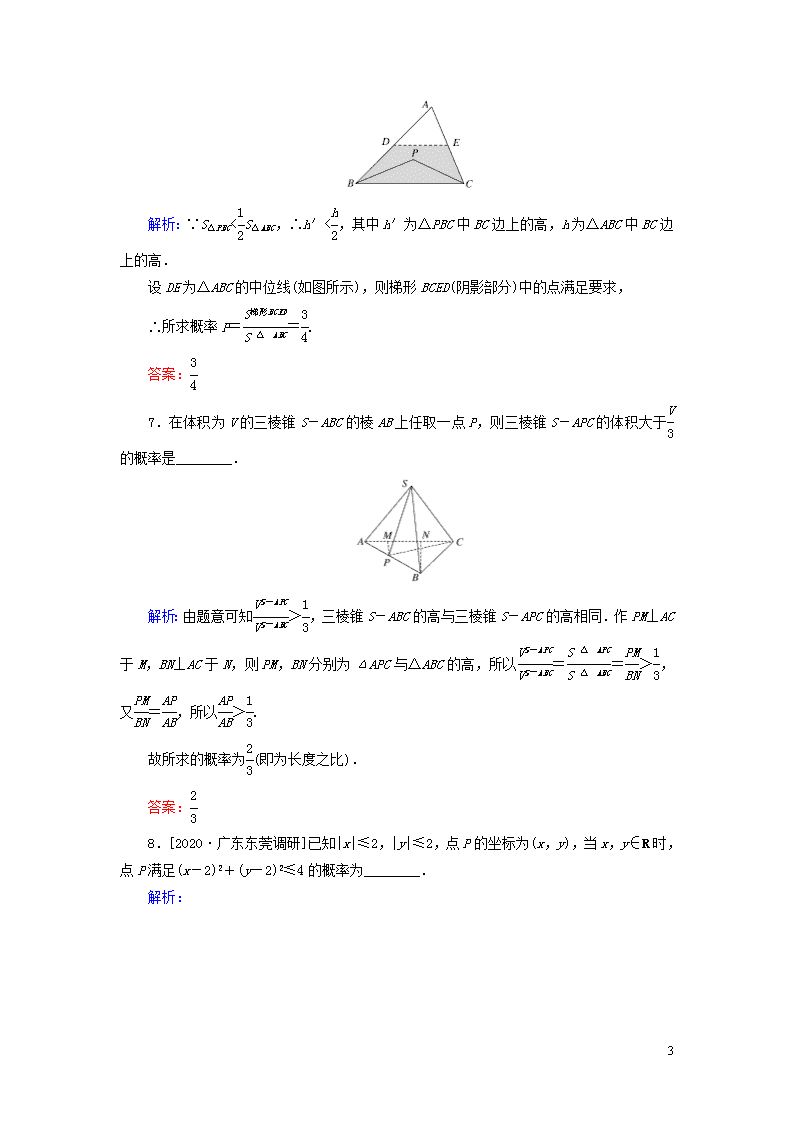
课时作业61　几何概型 ‎ [基础达标]‎ 一、选择题 ‎1．[2020·武汉调研]在长为16 cm的线段MN上任取一点P，以MP、NP为邻边作一矩形，则该矩形的面积大于60 cm2的概率为(　　)‎ A. B. C. D. 解析：本题考查几何概型．设MP＝x，则NP＝16－x，由x(16－x)＞60，解得6＜x＜10，所以所求概率P＝＝，故选A.‎ 答案：A ‎2.‎ 如图所示，矩形ABCD中，点E为边AB的中点，若在矩形ABCD内部随机取一个点Q，则点Q取自△AED或△BEC内部的概率等于(　　)‎ A. B. C. D. 解析：点Q取自△AED或△BEC内部的概率P＝＝.故选A.‎ 答案：A ‎3．在棱长为2的正方体ABCD－A1B1C1D1中，点O为底面ABCD的中心，在正方体ABCD－A1B1C1D1内随机取一点P，则点P到点O的距离大于1的概率为(　　)‎ A. B．1－ C. D．1－ 解析：点P到点O的距离大于1的点位于以O为球心，以1为半径的半球外．记“点P到点O的距离大于1”为事件M，则P(M)＝＝1－.‎ 7‎ 答案：B ‎4.‎ ‎[2020·河北九校联考]如图，矩形的长为6，宽为4，在矩形内随机撒300颗黄豆，落在椭圆外的黄豆数为96，以此试验数据为依据可以估计出椭圆的面积为(　　)‎ A．16.32 B．15.32‎ C．8.68 D．7.68‎ 解析：由题意，可估计椭圆的面积为×6×4＝16.32.故选A.‎ 答案：A ‎5．[2020·福建泉州泉港一中测试]若1路、2路公交车的站点均包括泉港一中，且1路公交车每10分钟一趟，2路公交车每20分钟一趟，则某学生去坐这2趟公交车回家，等车不超过5分钟的概率是(　　)‎ A. B. C. D. 解析：‎ 设1路公交车到达的时间为x,2路公交车到达的时间为y.(x，y)可以看成平面上的点，则可设Ω＝{(x，y)|0≤x≤10且0≤y≤20}，表示的是一个长方形区域，如图，其面积S＝10×20＝200.若某学生等车时间不超过5分钟，则其构成的平面区域为图中的阴影部分，面积S′＝125，故所求概率P＝＝＝，故选C.‎ 答案：C 二、填空题 ‎6．向面积为S的△ABC内任意投掷一点P，则△PBC的面积小于的概率为________．‎ 7‎ 解析：∵S△PBC0，函数y＝kx＋b的图象不经过第四象限的条件是b≥0.作出(k，b)对应的平面区域如图中的梯形ABCD(不含b轴)，其面积是S1＝＝，符合限制条件的(k，b)对应的平面区域如图中的三角形BOC，其面积是S2＝，故所求概率P＝＝.‎ ‎10．已知袋子中放有大小和形状相同的小球若干，其中标号为0的小球1个，标号为1的小球1个，标号为2的小球n个．若从袋子中随机抽取1个小球，取到标号是2的小球的概率是.‎ ‎(1)求n的值；‎ ‎(2)从袋子中不放回地随机抽取2个小球，记第一次取出的小球标号为a，第二次取出的小球标号为b.‎ ‎①记“2≤a＋b≤3”为事件A，求事件A的概率；‎ ‎②在区间[0,2]内任取2个实数x，y，求事件“x2＋y2>(a－b)2恒成立”的概率．‎ 解析：(1)依题意共有(n＋2)个小球，则从袋子中随机抽取1个小球，取到标号为2的小球的概率为＝，‎ 7‎ ‎∴n＝2.‎ ‎(2)①从袋子中不放回地随机抽取2个小球共有12种结果，而满足2≤a＋b≤3的结果有8种，‎ 故P(A)＝＝.‎ ‎②易知(a－b)2≤4，故待求概率的事件即为“x2＋y2>4”，(x，y)可以看成平面中的点的坐标，‎ 则全部结果所构成的区域为Ω＝{(x，y)|0≤x≤2,0≤y≤2，x，y∈R}，‎ 由几何概型得概率P＝＝1－.‎ ‎[能力挑战]‎ ‎11．[2020·福州四校联考]如图，在圆心角为90°的扇形AOB中，以圆心O为起点在上任取一点C作射线OC，则使得∠AOC和∠BOC都不小于30°的概率是(　　)‎ A. B. C. D. 解析：‎ 记事件T是“作射线OC，使得∠AOC和∠BOC都不小于30°”，如图，记的三等分点为M，N，连接OM，ON，则∠AON＝∠BOM＝∠MON＝30°，则符合条件的射线OC应落在扇形MON中，所以P(T)＝＝＝，故选A.‎ 答案：A ‎12.‎ 7‎ ‎[2020·黑龙江齐齐哈尔检测]随着计算机的出现，图标被赋予了新的含义，有了新的用武之地．在计算机应用领域，图标成了具有明确指代含义的计算机图形．如图所示的图标是一种被称为“黑白太阳”的图标，该图标共分为三部分．第一部分为外部的八个全等的矩形，每一个矩形的长为3、宽为1；第二部分为圆环部分，大圆半径为3，小圆半径为2；第三部分为圆环内部的白色区域．在整个“黑白太阳”图标中随机取一点，则此点取自图标第三部分的概率为(　　)‎ A. B. C. D. 解析：图标第一部分的面积为8×3×1＝24，图标第二部分的面积和第三部分的面积和为π×32＝9π，图标第三部分的面积为π×22＝4π，故此点取自图标第三部分的概率为，故选B.‎ 答案：B ‎13.‎ ‎[2020·湖南株洲联考]如图，三国时期数学家赵爽在《周髀算经》中利用弦图，给出了勾股定理的绝妙证明．图中包含四个全等的直角三角形及一个小正方形(阴影部分)．设直角三角形有一内角为30°，若向弦图内随机抛掷1 000颗米粒(大小忽略不计)，则落在小正方形(阴影部分)内的米粒数大约为(≈1.732)(　　)‎ A．134 B．866‎ C．300 D．500‎ 解析：设大正方形的边长为2x，则小正方形的边长为x－x，向弦图内随机抛掷1 000颗米粒(大小忽略不计)，设落在小正方形(阴影部分)内的米粒数大约为a，则＝，解得a＝1 000×≈134.故选A.‎ 答案：A 7‎ 7‎