【数学】西藏林芝市第二高级中学2019-2020学年高二下学期第二学段考试（期末考试）（文）试题（解析版）

【数学】西藏林芝市第二高级中学2019-2020学年高二下学期第二学段考试（期末考试）（文）试题（解析版）

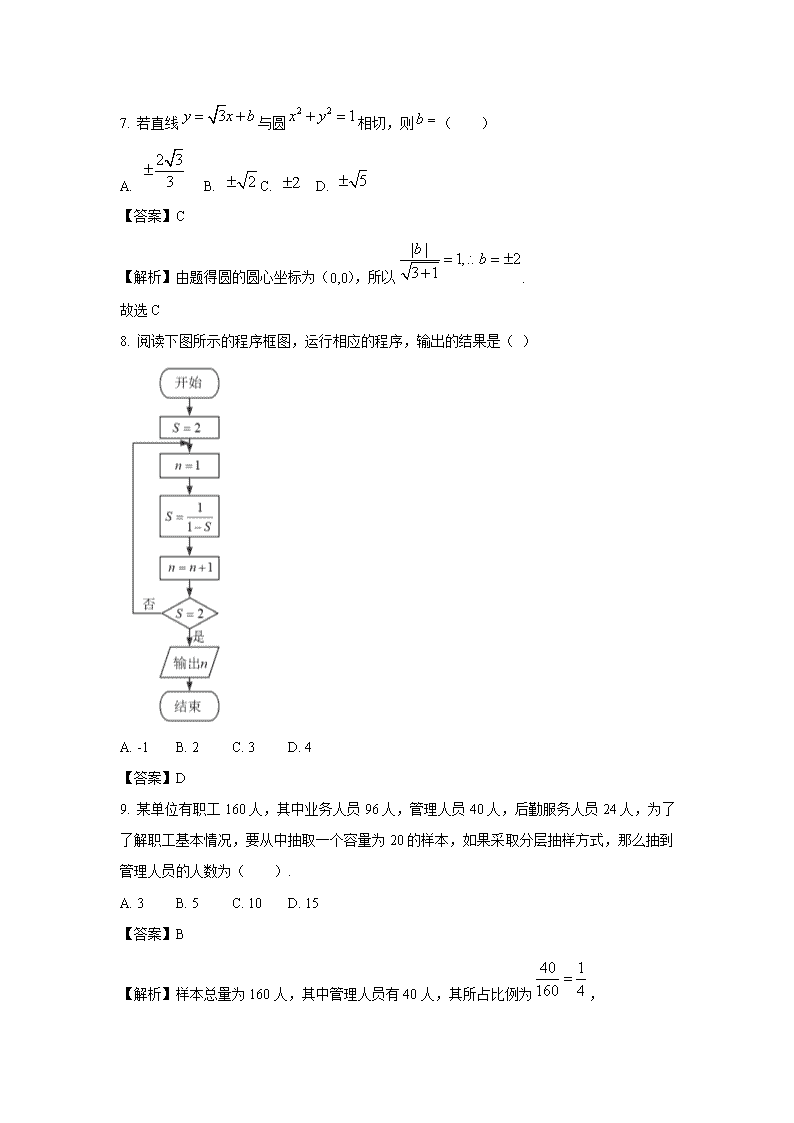
西藏林芝市第二高级中学2019-2020学年高二下学期 第二学段考试（期末考试）（文）试题 第I卷（选择题)‎ 一、单选题（每小题5分，共60分）‎ ‎1. 已知集合，则=（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】，则，‎ 故.‎ 故选：D ‎ ‎2. 函数 的定义域是（ ）‎ A. （0，2） B. （-∞，4] C. （0，4] D. （4，）‎ ‎【答案】C ‎【解析】函数的定义域满足：，‎ ‎∴，解得.‎ 故选：C.‎ ‎3. 已知函数，若，则的值为（ ）‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】函数定义域为R，‎ ‎，‎ 函数为奇函数，则.‎ 故选：B.‎ ‎4. 已知，， ，则（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】,‎ ‎,,‎ 故选：D ‎5. 直线的倾斜角为（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】设直线的倾斜角为．‎ 直线的点斜式方程是，‎ 直线的斜率．‎ ‎，，．‎ 故选：D．‎ ‎6. 设，则以线段为直径的圆的方程是（ ）‎ A. B. ‎ C. D. ‎ ‎【答案】A ‎【解析】的中点坐标为，圆的半径为，‎ 所以圆的方程为.‎ 故选：A.‎ ‎7. 若直线与圆相切，则（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】由题得圆的圆心坐标为（0,0），所以.‎ 故选C ‎8. 阅读下图所示的程序框图，运行相应的程序，输出的结果是（ ）‎ A. -1 B. ‎2 ‎C. 3 D. 4‎ ‎【答案】D ‎9. 某单位有职工160人，其中业务人员96人，管理人员40人，后勤服务人员24人，为了了解职工基本情况，要从中抽取一个容量为20的样本，如果采取分层抽样方式，那么抽到管理人员的人数为（ ）.‎ A. 3 B. ‎5 ‎C. 10 D. 15‎ ‎【答案】B ‎【解析】样本总量为160人，其中管理人员有40人，其所占比例为，‎ 现抽取一个容量为20的样本，抽到管理人员的人数为人.‎ 故选：B ‎10. 如图，边长为2的正方形中有一阴影区域，在正方形中随机撒一粒豆子，它落在阴影区域内的概率为.则阴影区域的面积约为 (　　)‎ A B. C. D. 无法计算 ‎【答案】C ‎【解析】设阴影区域的面积为，，所以.‎ 故选C.‎ ‎【点睛】本题考查几何概型的应用，属基础题.‎ ‎11. 函数的最小正周期是（ ）‎ A. 1 B. ‎2 ‎C. 3 D. 4‎ ‎【答案】B ‎【解析】函数的最小正周期是，‎ 故选：B．‎ ‎12. 已知向量，，则与的夹角为（ ）‎ A. B. C. D. ‎ ‎【答案】A ‎【解析】；；‎ 又；与夹角为．‎ 故选A．‎ 第II卷（非选择题)‎ 二、填空题（每小题5分，共20分）‎ ‎13. 已知函数的图象上每个点向左平移个单位长度得到函数的图象，则的值为_______.‎ ‎【答案】‎ ‎【解析】把函数的图象上每个点向左平移个单位长度， 得到函数的图象，，则， 故答案为．‎ ‎14. 已知，则__________．‎ ‎【答案】‎ ‎【解析】，，‎ 故答案为：．‎ ‎15. 直线与圆相交于，两点，则的长度等于__________.‎ ‎【答案】‎ ‎【解析】圆心，半径为，‎ 圆心到直线的距离为，‎ ‎.‎ 故答案为：.‎ ‎16. 点到直线的距离不大于4，则的取值范围是________．‎ ‎【答案】‎ ‎【解析】依题意可知，，解得．‎ 故答案为：．‎ 三、解答题（共70分）‎ ‎17.某赛季，甲、乙两名篮球运动员都参加了7场比赛，他们所有比赛得分的情况用如图所示的茎叶图表示．‎ ‎（Ⅰ）求甲、乙两名运动员得分的中位数；‎ ‎（Ⅱ）你认为哪位运动员的成绩更稳定？‎ ‎（Ⅲ）如果从甲、乙两位运动员的7场得分中各随机抽取一场的得分，求甲的得分大于乙的得分的概率．‎ ‎【解】（Ⅰ）运动员甲得分的中位数是22，运动员乙得分的中位数是23………2分 ‎（Ⅱ）…………………3分 ‎…………………4分 ‎…………………………………………………………………………………5分 ‎ ‎……………………………………………………………………………………………6分 ‎，从而甲运动员的成绩更稳定………………………………7分 ‎（Ⅲ）从甲、乙两位运动员的7场得分中各随机抽取一场的得分的基本事件总数为49‎ ‎……8分 其中甲的得分大于乙的是：甲得14分有3场，甲得17分有3场，甲得15分有3场 甲得24分有4场，甲得22分有3场，甲得23分有3场，甲得32分有7场，共计26场 ……………10分 从而甲的得分大于乙的得分的概率为………………………………12分 ‎18. 已知函数的部分图象如图所示．‎ ‎（1）求的解析式．‎ ‎（2）写出的递增区间．‎ ‎【解】（1）易知，，‎ ‎∴，∴，‎ 将点代入得，，，‎ ‎∴，，‎ ‎∵，∴，∴；‎ ‎（2）由，，‎ 解得，，‎ ‎∴的递增区间为，．‎ ‎19. 已知，.‎ ‎（1）求的值；‎ ‎（2）求的值.‎ ‎【解】（1），，‎ 因此，；‎ ‎（2）原式.‎ ‎20. 已知向量，向量.‎ ‎（1）求向量的坐标； ‎ ‎（2）当何值时，向量与向量共线.‎ ‎【解】（1）‎ ‎（2），‎ ‎∵与共线，∴∴‎ ‎21. 已知点、，直线.‎ ‎（1）求线段的中点坐标及直线的斜率；‎ ‎（2）若直线过点，且与直线平行，求直线的方程.‎ ‎【解】（1）根据题意，设的中点坐标为，‎ 又由点、，则，，‎ 所以，线段的中点坐标为，直线的斜率为；‎ ‎（2）设直线的方程为，‎ 又由直线经过点，则有，则.‎ 即直线的方程为.‎ ‎22. 已知圆心为C（4，3）的圆经过原点O．‎ ‎（1）求圆C的方程；‎ ‎（2）设直线3x﹣4y+15＝0与圆C交于A，B两点，求△ABC的面积．‎ ‎【解】（1）圆C的半径为 ，‎ 从而圆C的方程为（x﹣4）2+（y﹣3）2＝25；‎ ‎（2）作CD⊥AB于D，则CD平分线段AB，‎ 在直角三角形ADC中，由点到直线的距离公式，得|CD|＝3，‎ 所以，所以|AB|＝2|AD|＝8，‎ 所以△ABC的面积．‎