- 2021-06-16 发布 |
- 37.5 KB |
- 13页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
【数学】2020届一轮复习人教版(理)第10章第7讲离散型随机变量及其分布列学案
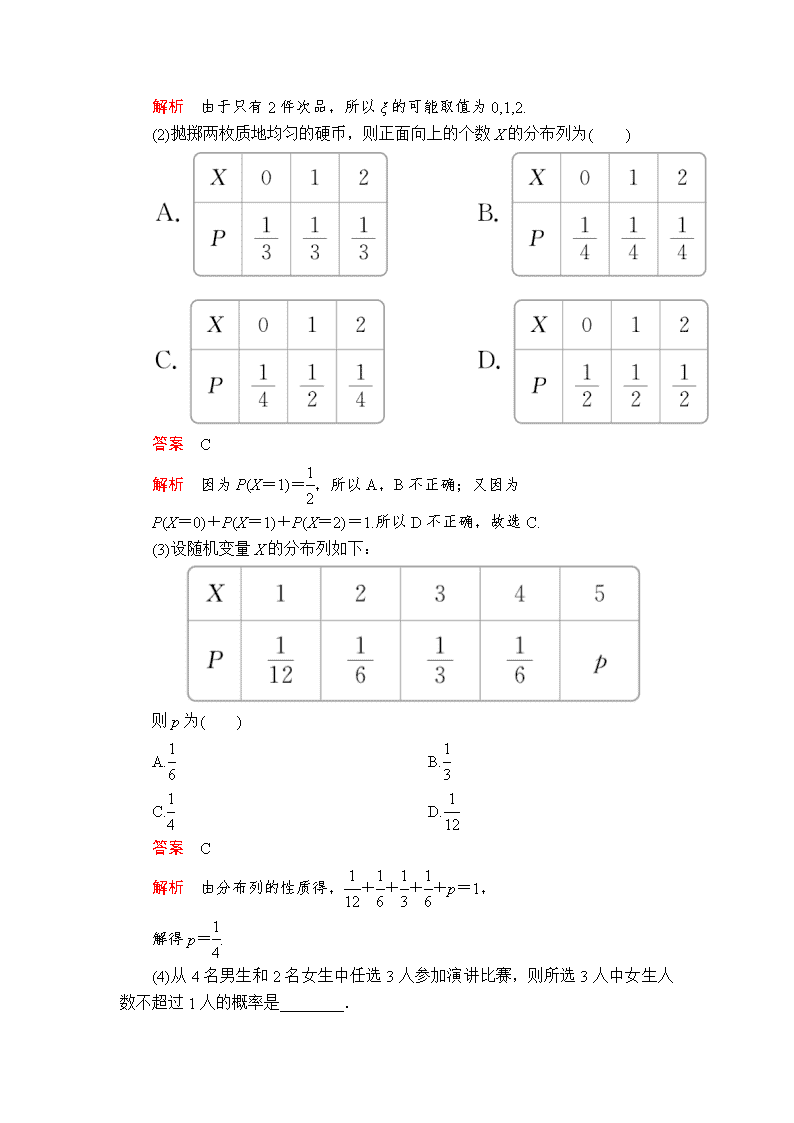
第7讲 离散型随机变量及其分布列 [考纲解读] 1.理解取有限个值的离散型随机变量及其分布列的概念,了解分布列对于刻画随机现象的重要性. 2.能确定随机变量,求出随机变量发生的概率,正确列出分布列.(重点、难点) 3.理解超几何分布,并能进行简单的应用. [考向预测] 从近三年高考情况来看,本讲一直是高考中的热点内容. 预测2020年将会考查:①与排列组合及统计知识结合的分布列;②与独立重复事件结合的分布列. 试题以解答题的形式呈现,以现实生活中的事例为背景进行考查,试题难度不大,属中档题型. 1.离散型随机变量 随着试验结果变化而变化的变量称为随机变量,常用字母X,Y,ξ,η,…表示.所有取值可以一一列出的随机变量,称为离散型随机变量. 2.离散型随机变量的分布列及性质 (1)一般地,若离散型随机变量X可能取的不同值为x1,x2,…,xi,…,xn,X取每一个值xi(i=1,2,…,n)的概率P(X=xi)=pi,则表 X x1 x2 … xi … xn P p1 p2 … pi … pn 称为离散型随机变量X的概率分布列,简称为X的分布列,有时为了表达简单,也用等式P(X=xi)=pi,i=1,2,…,n表示X的分布列. (2)离散型随机变量的分布列的性质 ①pi≥0(i=1,2,…,n); ②. 3.常见离散型随机变量的分布列 (1)两点分布 若随机变量X服从两点分布,即其分布列为 (2)超几何分布 在含有M件次品的N件产品中,任取n件,其中恰有X件次品,则P(X=k)=,k=0,1,2,…,m,其中m=min{M,n},且n≤N,M≤N,n,M,N∈N*. 如果随机变量X的分布列具有上表的形式,则称随机变量X服从超几何分布. 1.概念辨析 (1)随机试验的结果与随机变量是一种映射关系,即每一个试验结果都有唯一的随机变量的值与之对应. ( ) (2)离散型随机变量的各个可能值表示的事件是彼此互斥的.( ) (3)离散型随机变量在某一范围内取值的概率等于它取这个范围内各个值的概率之和.( ) (4)若随机变量X的分布列由下表给出, X 2 5 P 0.3 0.7 则它服从两点分布.( ) 答案 (1)√ (2)√ (3)√ (4)× 2.小题热身 (1)已知8件产品中有2件次品,从中任取3件,取到次品的件数为随机变量ξ,那么ξ的可能取值为( ) A.0,1 B.1,2 C.0,1,2 D.0,1,2,3 答案 C 解析 由于只有2件次品,所以ξ的可能取值为0,1,2. (2)抛掷两枚质地均匀的硬币,则正面向上的个数X的分布列为( ) 答案 C 解析 因为P(X=1)=,所以A,B不正确;又因为 P(X=0)+P(X=1)+P(X=2)=1.所以D不正确,故选C. (3)设随机变量X的分布列如下: 则p为( ) A. B. C. D. 答案 C 解析 由分布列的性质得,++++p=1, 解得p=. (4)从4名男生和2名女生中任选3人参加演讲比赛,则所选3人中女生人数不超过1人的概率是________. 答案 解析 设所选女生人数为x,则x服从超几何分布, 其中N=6,M=2,n=3,则 P(x≤1)=P(x=0)+P(x=1)=+=. 题型 离散型随机变量分布列的性质 设随机变量ξ的分布列P=ak(k=1,2,3,4,5). (1)求常数a的值; (2)求P; (3)求P. 解 由已知分布列为: (1)由a+2a+3a+4a+5a=1,得a=. (2)P=P+P+P(ξ=1)=++=. (3)因为<ξ<只有ξ=,,满足, 故P =P+P+P =++=. 条件探究 若将举例说明条件变为“P(ξ=n)=(n=1,2,3,4).”求P的值. 解 ∵P(ξ=n)=. ∴+++=1,∴a=. P=P(ξ=1)+P(ξ=2)=. 结论探究 举例说明条件下,求5ξ-1的分布列. 解 由举例说明解析得ξ的分布列为 所以5ξ-1的分布列为 1.分布列性质的两个作用 (1)利用分布列中各事件概率之和为1可求参数的值及检查分布列的正确性. (2)随机变量X所取的值分别对应的事件是两两互斥的,利用这一点可以求随机变量在某个范围内的概率. 提醒:求分布列中的参数值时,要保证每个概率值均为非负数. 2.随机变量X的线性组合的概率及分布列问题 (1)随机变量X的线性组合η=aX+b(a,b∈R)是随机变量. (2)求η=aX+b的分布列可先求出相应随机变量的值,再根据对应的概率写出分布列. 1.设离散型随机变量ξ的分布列如下表所示: 则下列各式正确的是( ) A.P(ξ<3)= B.P(ξ>1)= C.P(2<ξ<4)= D.P(ξ<0.5)=0 答案 C 解析 由离散型随机变量ξ的概率分布列得, P(ξ<3)=P(ξ=-1)+P(ξ=0)+P(ξ=1)+P(ξ=2) =+++=,故A错误;P(ξ>1)=P(ξ=2)+P(ξ=3)=+=,故B错误;P(2<ξ<4)=P(ξ=3)=,故C正确;P(ξ<0.5)=P(ξ=-1)+P(ξ=0)=+=,故D错误. 2.设X是一个离散型随机变量,其分布列为: 则q的值为( ) A.1 B.± C.- D.+ 答案 C 解析 由分布列的性质知 解得q=-. 题型 超几何分布 (2018·济南模拟)某外语学校的一个社团中有7名同学,其中2人只会法语,2人只会英语,3人既会法语又会英语,现选派3人到法国的学校交流访问.求: (1)在选派的3人中恰有2人会法语的概率; (2)在选派的3人中既会法语又会英语的人数X的分布列. 解 (1)设事件A:选派的3人中恰有2人会法语, 则P(A)==. (2)依题意知,X服从超几何分布,X的可能取值为0,1,2,3, P(X=0)==, P(X=1)==, P(X=2)==, P(X=3)==, ∴X的分布列为 1.超几何分布的两个特点 (1)超几何分布是不放回抽样问题. (2)随机变量为抽到的某类个体的个数. 2.超几何分布的应用条件 (1)考察对象分两类. (2)已知各类对象的个数. (3)从中抽取若干个个体,考察某类个体个数ξ的概率分布. 3.求超几何分布的分布列的步骤 某高校一专业在一次自主招生中,对20名已经选拔入围的学生进行语言表达能力和逻辑思维能力测试,结果如下表: 由于部分数据丢失,只知道从这20名参加测试的学生中随机抽取一人,抽到语言表达能力优秀或逻辑思维能力优秀的学生的概率为. (1)从参加测试的语言表达能力良好的学生中任意抽取2名,求其中至少有一名逻辑思维能力优秀的学生的概率; (2)从参加测试的20名学生中任意抽取2名,设语言表达能力优秀或逻辑思维能力优秀的学生人数为X,求随机变量X的分布列. 解 (1)用A表示“从这20名参加测试的学生中随机抽取一人,抽到语言表达能力优秀或逻辑思维能力优秀的学生”, ∵语言表达能力优秀或逻辑思维能力优秀的学生共有(6+n)名, ∴P(A)==,解得n=2, ∴m=4, 用B表示“从参加测试的语言表达能力良好的学生中任意抽取2名,其中至少有一名逻辑思维能力优秀的学生”, ∴P(B)=1-=. (2)随机变量X服从超几何分布,X的可能取值为0,1,2. ∵在20名学生中,语言表达能力优秀或逻辑思维能力优秀的学生共有8名, ∴P(X=0)==, P(X=1)==, P(X=2)==, ∴X的分布列为 X 0 1 2 P 题型 求离散型随机变量的分布列 角度1 与互斥事件有关的分布列问题 1.已知2件次品和3件正品混放在一起,现需要通过检测将其区分,每次随机检测一件产品,检测后不放回,直到检测出2件次品或者检测出3件正品时检测结束. (1)求第一次检测出的是次品且第二次检测出的是正品的概率; (2)已知每检测一件产品需要费用100元,设X表示直到检测出2件次品或者检测出3件正品时所需要的检测费用(单位:元),求X的分布列和均值(数学期望). 解 (1)记第一次检测出的是次品且第二次检测出的是正品为事件A, 则P(A)==. (2)X的可能取值为200,300,400. P(X=200)==, P(X=300)==, P(X=400)=1-P(X=200)-P(X=300)=1--=. 故X的分布列为 X 200 300 400 P E(X)=200×+300×+400×=350. 角度2 与统计有关的分布列的求法 2.随着经济模式的改变,微商和电商已成为当今城乡一种新型的购销平台.已知经销某种商品的电商在任何一个销售季度内,每售出1吨该商品可获利润0.5万元,未售出的商品,每1吨亏损0.3万元.根据往年的销售经验,得到一个销售季度内市场需求量的频率分布直方图如图所示.已知电商为下一个销售季度筹备了130吨该商品,现以x(单位:吨,100≤x≤150)表示下一个销售季度的市场需求量,T(单位:万元)表示该电商下一个销售季度内经销该商品获得的利润. (1)视x分布在各区间内的频率为相应的概率,求P(x≥120); (2)将T表示为x的函数,求出该函数表达式; (3)在频率分布直方图的市场需求量分组中,以各组的区间中点值(组中值)代表该组的各个值,并以市场需求量落入该区间的频率作为市场需求量取该组中值的概率(例如x∈[100,110),则取x=105的概率等于市场需求量落入[100,110)的频率),求T的分布列. 解 (1)根据频率分布直方图及两两互斥事件的概率的可加性得, P(x≥120)=P(120≤x<130)+P(130≤x<140)+P(140≤x≤150) =0.030×10+0.025×10+0.015×10=0.7. (2)当x∈[100,130)时,T=0.5x-0.3(130-x)=0.8x-39; 当x∈[130,150]时,T=0.5×130=65, 所以T= (3)由题意及(2)可得, 当x∈[100,110)时,T=0.8×105-39=45,P(T=45)=0.010×10=0.1; 当x∈[110,120)时,T=0.8×115-39=53, P(T=53)=0.020×10=0.2; 当x∈[120,130)时,T=0.8×125-39=61,P(T=61)=0.030×10=0.3; 当x∈[130,150]时,T=65,P(T=65)=(0.025+0.015)×10=0.4; 所以T的分布列为 T 45 53 61 65 P 0.1 0.2 0.3 0.4 所以E(T)=45×0.1+53×0.2+61×0.3+65×0.4=59.4万元. 离散型随机变量分布列的求解步骤 (1)明取值:明确随机变量的可能取值有哪些,且每一个取值所表示的意义. (2)求概率:要弄清楚随机变量的概率类型,利用相关公式求出变量所对应的概率. (3)画表格:按规范要求形式写出分布列. (4)做检验:利用分布列的性质检验分布列是否正确. 提醒:求随机变量某一范围内取值的概率,要注意它在这个范围内的概率等于这个范围内各概率值的和. 1.某小组共10人,利用假期参加义工活动,已知参加义工活动次数为1,2,3的人数分别为3,3,4,现从这10人中随机选出2人作为该组代表参加座谈会. (1)设A为事件“选出的2人参加义工活动次数之和为4”,求事件A发生的概率; (2)设X为选出的2人参加义工活动次数之差的绝对值,求随机变量X的分布列. 解 (1)由已知,有P(A)==. 所以事件A发生的概率为. (2)随机变量X的所有可能取值为0,1,2. P(X=0)==, P(X=1)==, P(X=2)==. 所以随机变量X的分布列为 X 0 1 2 P 2.甲、乙两家外卖公司,其送餐员的日工资方案如下:甲公司的底薪70元,每单抽成4元;乙公司无底薪,40单以内(含40单)的部分每单抽成5元,超出40单的部分每单抽成7元,假设同一公司送餐员一天的送餐单数相同,现从两家公司各随机抽取一名送餐员,并分别记录其100天的送餐单数,得到如下频数表: 甲公司送餐员送餐单数频数表 送餐单数 38 39 40 41 42 天数 20 40 20 10 10 乙公司送餐员送餐单数频数表 送餐单数 38 39 40 41 42 天数 10 20 20 40 10 (1)现从甲公司记录的100天中随机抽取两天,求这两天送餐单数都大于40的概率; (2)若将频率视为概率,回答下列问题: ①记乙公司送餐员日工资为X(单位:元),求X的分布列和数学期望; ②小明拟到甲、乙两家公司中的一家应聘送餐员,如果仅从日工资的角度考虑,请利用所学的统计学知识为他作出选择,并说明理由. 解 (1)记“抽取的两天送餐单数都大于40”为事件M, 则P(M)==. (2)①设乙公司送餐员送餐单数为a, 则当a=38时,X=38×5=190, 当a=39时,X=39×5=195, 当a=40时,X=40×5=200, 当a=41时,X=40×5+1×7=207, 当a=42时,X=40×5+2×7=214. 则X的所有可能取值为190,195,200,207,214. 所以X的分布列为 X 190 195 200 207 214 P 故E(X)=190×+195×+200×+207×+214×=. ②依题意,甲公司送餐员日平均送餐单数为 38×0.2+39×0.4+40×0.2+41×0.1+42×0.1=39.5. 所以甲公司送餐员日平均工资为70+4×39.5=228(元). 由①得乙公司送餐员日平均工资为202.2元. 因为202.2<228,故推荐小明去甲公司应聘.查看更多