【数学】2019届一轮复习全国经典版（理）参数方程学案

【数学】2019届一轮复习全国经典版（理）参数方程学案

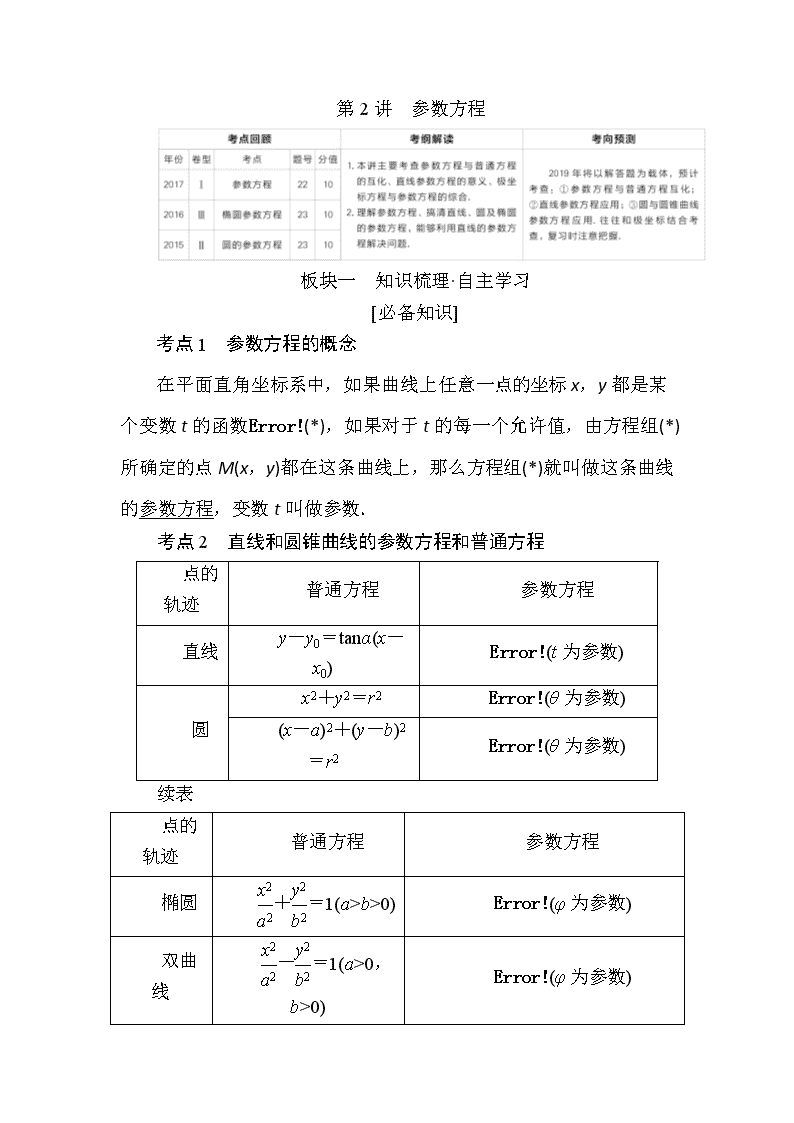
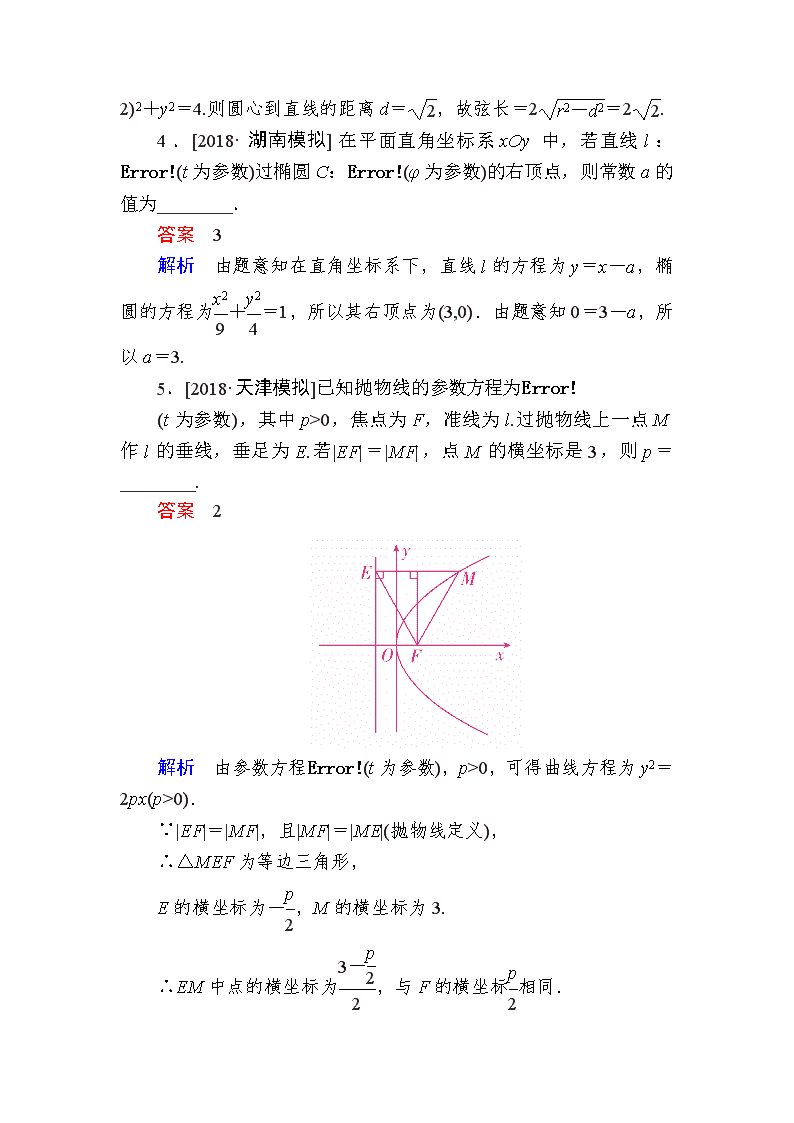
第2讲　参数方程 板块一　知识梳理·自主学习 ‎[必备知识]‎ 考点1　参数方程的概念 在平面直角坐标系中，如果曲线上任意一点的坐标x，y都是某个变数t的函数(*)，如果对于t的每一个允许值，由方程组(*)所确定的点M(x，y)都在这条曲线上，那么方程组(*)就叫做这条曲线的参数方程，变数t叫做参数．‎ 考点2　直线和圆锥曲线的参数方程和普通方程 点的轨迹 普通方程 参数方程 直线 y－y0＝tanα(x－x0)‎ (t为参数)‎ 圆 x2＋y2＝r2‎ (θ为参数)‎ ‎(x－a)2＋(y－b)2＝r2‎ (θ为参数)‎ 续表 点的轨迹 普通方程 参数方程 椭圆 ＋＝1(a>b>0)‎ (φ为参数)‎ 双曲线 －＝1(a>0，b>0)‎ (φ为参数)‎ 抛物线 y2＝2px (t为参数)‎ ‎ [考点自测]‎ ‎1．判断下列结论的正误．(正确的打“√”，错误的打“×”)‎ ‎(1)参数方程(t≥1)表示的曲线为直线．(　　)‎ ‎(2)直线y＝x与曲线(α为参数)的交点个数为1.(　　)‎ ‎(3)直线(t为参数)的倾斜角α为30°.(　　)‎ ‎(4)参数方程表示的曲线为椭圆．(　　)‎ 答案　(1)×　(2)×　(3)√　(4)×‎ ‎2．已知圆的参数方程(θ为参数)，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，直线的极坐标方程为3ρcosα－4ρsinα－9＝0，则直线与圆的位置关系是(　　)‎ A．相切 B．相离 C．直线过圆心 D．相交但直线不过圆心 答案　D 解析　圆的普通方程为x2＋y2＝4，直线的直角坐标方程为3x－4y－9＝0.圆心(0,0)到直线的距离d＝＝<2，所以直线与圆相交．显然直线不过原点(0,0)．故选D.‎ ‎3．[2018·安徽模拟]以平面直角坐标系的原点为极点，x轴的正半轴为极轴，建立极坐标系，两种坐标系中取相同的长度单位．已知直线l的参数方程是(t为参数)，圆C的极坐标方程是ρ＝4cosθ，则直线l被圆C截得的弦长为(　　)‎ A. B．2 ‎ C. D．2 答案　D 解析　由题意得直线l的方程为x－y－4＝0，圆C的方程为(x－2)2＋y2＝4.则圆心到直线的距离d＝，故弦长＝2＝2.‎ ‎4．[2018·湖南模拟]在平面直角坐标系xOy中，若直线l：(t为参数)过椭圆C：(φ为参数)的右顶点，则常数a的值为________．‎ 答案　3‎ 解析　由题意知在直角坐标系下，直线l的方程为y＝x－a，椭圆的方程为＋＝1，所以其右顶点为(3,0)．由题意知0＝3－a，所以a＝3.‎ ‎5．[2018·天津模拟]已知抛物线的参数方程为 ‎(t为参数)，其中p>0，焦点为F，准线为l.过抛物线上一点M作l的垂线，垂足为E.若|EF|＝|MF|，点M的横坐标是3，则p＝________.‎ 答案　2‎ 解析　由参数方程(t为参数)，p>0，可得曲线方程为y2＝2px(p>0)．‎ ‎∵|EF|＝|MF|，且|MF|＝|ME|(抛物线定义)，‎ ‎∴△MEF为等边三角形，‎ E的横坐标为－，M的横坐标为3.‎ ‎∴EM中点的横坐标为，与F的横坐标相同．‎ ‎∴＝，∴p＝2.‎ ‎6．[2015·湖北高考]在直角坐标系xOy中，以O为极点，x轴的正半轴为极轴建立极坐标系．已知直线l的极坐标方程为ρ(sinθ－3cosθ)＝0，曲线C的参数方程为(t为参数)，l与C相交于A，B两点，则|AB|＝________.‎ 答案　2 解析　因为ρ(sinθ－3cosθ)＝0，所以ρsinθ＝3ρcosθ，所以y＝3x.由消去t得y2－x2＝4.由解得或不妨令A，B，由两点间的距离公式得|AB|＝＝2.‎ 板块二　典例探究·考向突破 考向　参数方程与普通方程的互化 例　1　[2017·全国卷Ⅰ]在直角坐标系xOy中，曲线C的参数方程为(θ为参数)，直线l的参数方程为(t为参数)．‎ ‎(1)若a＝－1，求C与l的交点坐标；‎ ‎(2)若C上的点到l距离的最大值为，求a.‎ 解　(1)曲线C的普通方程为＋y2＝1.‎ 当a＝－1时，直线l的普通方程为x＋4y－3＝0.‎ 由 解得或 从而C与l的交点坐标为(3,0)，.‎ ‎(2)直线l的普通方程为x＋4y－a－4＝0，故C上的点(3cosθ，sinθ)到l的距离为d＝ ‎＝，‎ 当a≥－4时，d的最大值为.‎ 由题设得＝，所以a＝8；‎ 当a＜－4时，d的最大值为.‎ 由题设得＝，‎ 所以a＝－16.‎ 综上，a＝8或a＝－16.‎ 触类旁通 将参数方程化为普通方程的方法 ‎(1)将参数方程化为普通方程，需要根据参数方程的结构特征，选取适当的消参方法．常见的消参方法有：代入消参法、加减消参法、平方消参法等，对于含三角函数的参数方程，常利用同角三角函数关系式消参，如sin2θ＋cos2θ＝1等．‎ ‎(2)将参数方程化为普通方程时，要注意两种方程的等价性，不要增解．‎ ‎【变式训练1】　[2018·湖南长郡中学模拟]已知曲线C1：(t为参数)，C2：(θ为参数)．‎ ‎(1)化C1，C2的方程为普通方程，并说明它们分别表示什么曲线；‎ ‎(2)若C1上的点P对应的参数为t＝，Q为C2上的动点，求PQ的中点M到直线C3：(t为参数)距离的最小值．‎ 解　(1)C1：(x＋4)2＋(y－3)2＝1，C2：＋＝1，‎ C1表示圆心是(－4,3)，半径是1的圆，C2表示中心是坐标原点，焦点在x轴上，长半轴长是8，短半轴长是3的椭圆．‎ ‎(2)当t＝时，P(－4,4)，又Q(8cosθ，3sinθ)，故M，‎ 又C3的普通方程为x－2y－7＝0，则M到C3的距离d＝|4cosθ－3sinθ－13|＝·|3sinθ－4cosθ＋13|＝|5sin(θ－φ)＋13|，‎ 所以d的最小值为.‎ 考向　直线的参数方程 例　2　[2018·泉州模拟]已知在平面直角坐标系xOy中，直线l的参数方程是(t是参数)，以平面直角坐标系的原点为极点，x轴的正半轴为极轴建立极坐标系，两种坐标系中取相同的单位长度，曲线C的极坐标方程为ρ＝4sin.‎ ‎(1)写出直线l的普通方程和曲线C的直角坐标方程；‎ ‎(2)设点P的直角坐标为(1,2)，直线l与曲线C的交点为A，B，试求|AB|及|PA|·|PB|的值．‎ 解　(1)直线l的普通方程为x＋y－3＝0.‎ ρ＝4sin＝4sinθ＋4cosθ，所以ρ2＝4ρsinθ＋4ρcosθ，所以曲线 C的直角坐标方程为x2＋y2－4x－4y＝0(或写成(x－2)2＋(y－2)2＝8)．‎ ‎(2)直线l的参数方程可化为(t′是参数)，‎ 把直线l的参数方程代入x2＋y2－4x－4y＝0得，t′2＋t′－7＝0.‎ 设A，B对应的参数分别为t1′，t2′，则t1′＋t2′＝－，t1′t2′＝－7，点P(1,2)显然在直线l上，故|AB|＝|t1′－t2′|＝＝，故|PA|·|PB|＝|t1′t2′|＝7.‎ 触类旁通 直线的参数方程的标准形式 过定点P0(x0，y0)，倾斜角为α的直线参数方程的标准形式为(t为参数)，t的几何意义是直线上的点P到点P0(x0，y0)的数量，即|t|＝|PP0|时为距离．使用该式时直线上任意两点P1、P2对应的参数分别为t1、t2，则|P1P2|＝|t1－t2|，P1P2的中点对应的参数为(t1＋t2)．‎ ‎【变式训练2】　[2018·哈尔滨模拟]在平面直角坐标系xOy中，直线l的参数方程为，以坐标原点O为极点，x轴的非负半轴为极轴建立极坐标系，已知圆C的圆心C的极坐标为，半径为2，直线l与圆C交于M，N两点．‎ ‎(1)求圆C的极坐标方程；‎ ‎(2)当φ变化时，求弦长|MN|的取值范围．‎ 解　(1)由已知，得圆心C的直角坐标为(1，)，半径为2，‎ ‎∴圆C的直角坐标方程为(x－1)2＋(y－)2＝4，‎ 即x2＋y2－2x－2y＝0，‎ ‎∵x＝ρcosθ，y＝ρsinθ，∴ρ2－2ρcosθ－2ρsinθ＝0，‎ 故圆C的极坐标方程为ρ＝4cos.‎ ‎(2)由(1)知，圆C的直角坐标方程为x2＋y2－2x－2y＝0，将直线的参数方程代入圆的直角坐标方程中得，‎ ‎(2＋tcosφ)2＋(＋tsinφ)2－2(2＋tcosφ)－2(＋tsinφ)＝0，‎ 整理得，t2＋2tcosφ－3＝0，‎ 设M，N两点对应的参数分别为t1，t2，则t1＋t2＝－2cosφ，t1·t2＝－3，‎ ‎∴|MN|＝|t1－t2|＝ ‎ ＝，‎ ‎∵φ∈，∴cosφ∈，∴|MN|∈[，4]．‎ 考向　极坐标、参数方程的综合应用 例　3　[2018·盐城模拟]已知直线l的参数方程为(t为参数)，以原点O为极点，x轴的正半轴为极轴建立极坐标系，曲线C的极坐标方程为ρ＝.‎ ‎(1)直接写出直线l的极坐标方程和曲线C的直角坐标方程；‎ ‎(2)过曲线C上任意一点P作与直线l夹角为的直线m，设直线m与直线l的交点为A，求|PA|的最大值．‎ 解　(1)由(t为参数)，得l的普通方程为2x＋y－6＝0，令x＝ρcosθ，y＝ρsinθ，得直线l的极坐标方程为2ρcosθ＋ρsinθ－6＝0，由曲线C的极坐标方程，知ρ2＋3ρ2cos2θ＝4，所以曲线C的直角坐标方程为x2＋＝1.‎ ‎(2)由(1)，知直线l的普通方程为2x＋y－6＝0，设曲线C上任意一点P(cosα，2sinα)，点P到直线l的距离d＝.‎ 由题意得|PA|＝＝，‎ ‎∴当sin＝－1时，|PA|取得最大值，最大值为.‎ 触类旁通 极坐标与参数方程综合应用中注意的问题 ‎(1)在已知极坐标方程求曲线交点、距离、线段长、切线等几何问题时，如果不能直接用极坐标解决，或用极坐标解决较麻烦时，可将极坐标方程转化为直角坐标方程解决．转化时要注意两坐标系的关系，注意ρ，θ的取值范围，取值范围不同对应的曲线不同．‎ ‎(2)解答参数方程的有关问题时，首先要弄清参数是谁，代表的几何意义是什么；其次要认真观察方程的表现形式，以便于寻找最佳化简途径．‎ ‎【变式训练3】　在直角坐标系xOy中，曲线C1的参数方程为(t为参数)，若以O为极点，x轴正半轴为极轴建立极坐标系，曲线C2的极坐标方程为ρcosθ＋2ρsinθ＋4＝0(ρ≥0)．‎ ‎(1)求曲线C1的普通方程与曲线C2的直角坐标方程；‎ ‎(2)若A是曲线C1上的任意一点，B是曲线C2上的任意一点，求线段AB的最小值．‎ 解　(1)由消去参数t，得曲线C1的普通方程为x2＝4y.‎ 将代入到ρcosθ＋2ρsinθ＋4＝0(ρ≥0)中，得x＋2y＋4＝0，‎ 即曲线C2的直角坐标方程为x＋2y＋4＝0.‎ ‎(2)解法一：因为A是曲线C1上的任意一点，B是曲线C2上的任意一点，所以线段AB的最小值，即与曲线C2平行的直线与曲线C1相切时，切点到曲线C2的距离，设切线的方程为x＋2y＋m＝0，‎ 由消去y得x2＋2x＋2m＝0，‎ 所以Δ＝22－4×1×2m＝0，得m＝，‎ 因此切点为，其到直线C2的距离d＝＝，即|AB|min＝.‎ 解法二：因为A是曲线C1上的任意一点，B是曲线C2上的任意一点，‎ 所以可设点A(4t,4t2)，线段AB的最小值即点A到直线C2的距离d的最小值，‎ 所以d＝＝，‎ 当t＝－时，dmin＝，即|AB|min＝.‎ 核心规律 参数方程与普通方程互化的方法 ‎(1)参数方程化为普通方程：化参数方程为普通方程的基本思路是消去参数，常用的消参方法有代入消去法、加减消去法、恒等式(三角的或代数的)消去法．‎ ‎(2)普通方程化为参数方程：化普通方程为参数方程的基本思路是引入参数，即选定合适的参数t，先确定一个关系x＝f(t)(或y＝φ(t))，再代入普通方程F(x，y)＝0，求得另一关系y＝φ(t)(或x＝f(t))．‎ 满分策略 参数方程应用中的注意事项 ‎(1)‎ 参数方程通过代入消元或加减消元消去参数化为普通方程，要注意普通方程与原参数方程的取值范围保持一致．‎ ‎(2)普通方程化为参数方程需要引入参数，选择的参数不同，所得的参数方程也不一样．一般地，常选择的参数有角、有向线段的数量、斜率，某一点的横坐标(或纵坐标)．‎ ‎(3)常见曲线的参数方程中的参数都有几何意义，注意利用几何意义常能够给解题带来方便.‎ 板块三　模拟演练·提能增分 ‎ [基础能力达标]‎ ‎1．[2017·江苏高考]在平面直角坐标系xOy中，已知直线l的参数方程为(t为参数)，曲线C的参数方程为(s为参数)．设P为曲线C上的动点，求点P到直线l的距离的最小值．‎ 解　直线l的普通方程为x－2y＋8＝0.‎ 因为点P在曲线C上，设P(2s2,2s)，‎ 从而点P到直线l的距离d＝ ‎＝.‎ 当s＝时，dmin＝.‎ 因此当点P的坐标为(4,4)时，曲线C上的点P到直线l的距离取到最小值.‎ ‎2．[2017·全国卷Ⅲ]在直角坐标系xOy中，直线l1的参数方程为(t为参数)，直线l2的参数方程为(m为参数)．设l1与l2的交点为P，当k变化时，P的轨迹为曲线C.‎ ‎(1)写出C的普通方程；‎ ‎(2)以坐标原点为极点，x轴正半轴为极轴建立极坐标系，设l3：ρ(cosθ＋sinθ)－＝0，M为l3与C的交点，求M的极径．‎ 解　(1)消去参数t得l1的普通方程l1：y＝k(x－2)；‎ 消去参数m得l2的普通方程l2：y＝(x＋2)．‎ 设P(x，y)，由题设得 消去k得x2－y2＝4(y≠0)，‎ 所以C的普通方程为x2－y2＝4(y≠0)．‎ ‎(2)C的极坐标方程为ρ2(cos2θ－sin2θ)＝4(0＜θ＜2π，θ≠π)，‎ 联立得 cosθ－sinθ＝2(cosθ＋sinθ)．‎ 故tanθ＝－，从而cos2θ＝，sin2θ＝.‎ 代入ρ2(cos2θ－sin2θ)＝4得ρ2＝5，‎ 所以交点M的极径为.‎ ‎3．[2018·安阳模拟]已知极坐标系的极点为直角坐标系xOy的原点，极轴为x轴的正半轴，两种坐标系中的长度单位相同，圆C的直角坐标系方程为x2＋y2＋2x－2y＝0，直线l的参数方程为(t为参数)，射线OM的极坐标方程为θ＝.‎ ‎(1)求圆C和直线l的极坐标方程；‎ ‎(2)已知射线OM与圆C的交点为O，P，与直线l的交点为Q，求线段PQ的长．‎ 解　(1)∵圆C的直角坐标系方程为x2＋y2＋2x－2y＝0，‎ ‎∴圆C的极坐标方程为ρ2＋2ρcosθ－2ρsinθ＝0，‎ 化简得ρ＋2cosθ－2sinθ＝0，即ρ＝2sin.‎ ‎∵直线l的参数方程为(t为参数)，‎ 消参得：x－y＋1＝0，‎ ‎∴直线l的极坐标方程为ρcosθ－ρsinθ＋1＝0，‎ 即ρ＝.‎ ‎(2)当θ＝时，|OP|＝2sin＝2，‎ 故点P的极坐标为，‎ ‎|OQ|＝＝＝，‎ 故点Q的极坐标为，‎ ‎|PQ|＝|OP|－|OQ|＝2－＝.‎ 故线段PQ的长为.‎ ‎4．[2018·长沙模拟]以直角坐标系的原点O为极点，x轴的正半轴为极轴，且两个坐标系取相等的长度单位．已知直线l的参数方程为(t为参数，0<φ<π)，曲线C的极坐标方程为ρcos2θ＝4sinθ.‎ ‎(1)求直线l的普通方程和曲线C的直角坐标方程；‎ ‎(2)设直线l与曲线C相交于A，B两点，当φ变化时，求|AB|的最小值．‎ 解　(1)由(t为参数，0<φ<π)，消去t，得xcosφ－ysinφ＋sinφ＝0，‎ 所以直线l的普通方程为xcosφ－ysinφ＋sinφ＝0.‎ 由ρcos2θ＝4sinθ，得(ρcosθ)2＝4ρsinθ，‎ 把x＝ρcosθ，y＝ρsinθ代入上式，得x2＝4y，‎ 所以曲线C的直角坐标方程为x2＝4y.‎ ‎(2)将直线l的参数方程代入x2＝4y，得t2sin2φ－4tcosφ－4＝0，‎ 设A，B两点对应的参数分别为t1，t2，‎ 则t1＋t2＝，t1t2＝－，‎ 所以|AB|＝|t1－t2|＝ ‎＝＝.‎ 当φ＝时，|AB|取得最小值，最小值为4.‎ ‎5．[2018·榆林模拟]在直角坐标系xOy中，曲线C的参数方程为(t为参数，a>0)．以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，已知直线l的极坐标方程为ρcos＝－2.‎ ‎(1)设P是曲线C上的一个动点，当a＝2时，求点P到直线l的距离的最小值；‎ ‎(2)若曲线C上的所有点均在直线l的右下方，求a的取值范围．‎ 解　(1)由ρcos＝－2，得(ρcosθ－ρsinθ)＝－2，‎ 化成直角坐标方程，得(x－y)＝－2，即直线l的方程为x－y＋4＝0.‎ 依题意，设P(2cost,2sint)，则点P到直线l的距离d＝＝.‎ 当t＋＝2kπ＋π，即t＝2kπ＋，k∈Z时，dmin＝2－2.‎ 故点P到直线l的距离的最小值为2－2.‎ ‎(2)∵曲线C上的所有点均在直线l的右下方，‎ ‎∴对∀t∈R，有acost－2sint＋4>0恒成立，‎ 即cos(t＋φ)>－4恒成立，‎ ‎∴<4，又a>0，∴00可知tanα＝.‎ 所以直线l的斜率为.‎