【数学】2019届一轮复习人教A版（理）立体几何学案

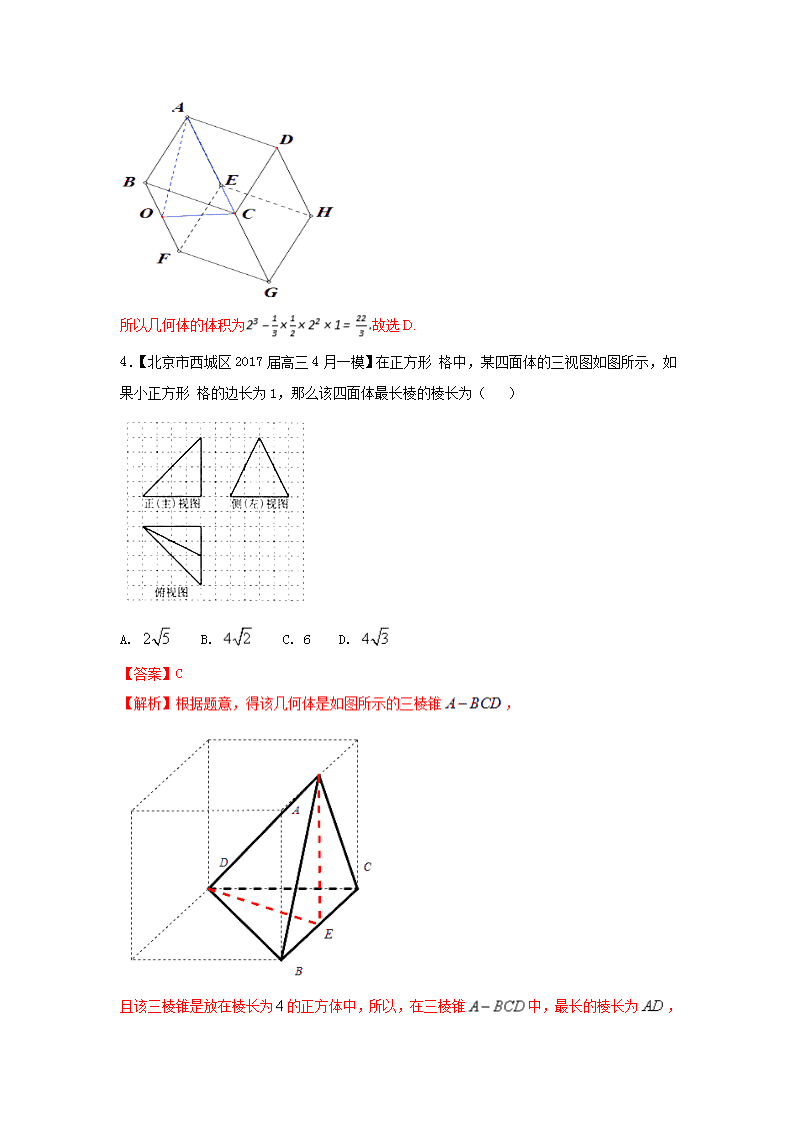
【数学】2019届一轮复习人教A版（理）立体几何学案

‎【热点知识再梳理——胸有成竹】‎ 热点一：三视图与表面积、体积 ‎[1] 几何体的三视图排列规则：俯视图放在正(主)视图下面，侧(左)视图放在正(主)视图右面，“长对正，高平齐，宽相等．” : , , ,X,X, ]‎ ‎[2] 以三视图为载体，考查面积、体积的计算，尤其三视图及柱、锥与球的接切问题相结合是考试的重点和热点，这类题的解决方法一般为将三视图还原几何体，再利用几何体的表面积公式或体积公式计算，解决的关键是要熟悉常见几何体的三视图，尤其注意几何体的不同摆放位置三视图会发生变化．由几何体的三视图确定几何体时，要注意以下几点：‎ ‎(1)还原后的几何体一般为较熟悉的柱、锥、台、球的组合体．‎ ‎(2)注意图中实、虚线，实际是原几何体中的可视线与被遮挡线．‎ ‎(3)想象原形，并画出草图后进行三视图还原，把握三视图和几何体之间的关系，与所给三视图比较，通过调整准确画出原几何体．‎ ‎[3]多面体与球接、切问题的求解策略 ‎(1)涉及球与棱柱、棱锥的接、切问题时，一般过球心及多面体中的特殊点(一般为接、切点)或线作截面，把空间问题转化为平面问题，再利用平面几何知识寻找几何体中元素间的关系，或只画内接、外切的几何体的直观图，确定球心的位置，弄清球的半径(直径)与该几何体已知量的关系，列方程(组)求解．‎ ‎(2)若球面上四点P，A，B，C构成的三条线段PA，PB，PC两两互相垂直，且PA＝a，PB＝b，PC＝c，一般把有关元素“补形”成为一个球内接长方体，则4R2＝a2＋b2＋c2求解．‎ ‎1．【湖北省荆州市2018届高三质量检查（III）】如图， 格纸上小正方形的边长为1，粗线画出的是某多面体的三视图，则该多面体的表面积为（ ）‎ A. B. C. D. 12‎ ‎【答案】C ‎【解析】由三视图可得，该几何体为如图所示的棱长为2的正方体中的四棱锥，且底面矩形中，．‎ 故该多面体的表面积为．选C． ‎ ‎2．在平面几何中，有“若的周长，面积为，则内切圆半径”，类比上述结论，在立体几何中，有“若四面体的表面积为，体积为，则其内切球的半径（ ） ‎ A. B. C. D. ‎ ‎【答案】A ‎ ‎ ‎3．【广东省肇庆市2018届高三第三次模拟】已知某几何体的三视图如图所示，则该几何体的体积为 A. B. C. D. ‎ ‎【答案】D ‎【解析】由三视图可知原几何体是在一个正方体的左上角割去了一个三棱锥O-ABC，‎ 所以几何体的体积为故选D. ‎ ‎4．【北京市西城区2017届高三4月一模】在正方形 格中，某四面体的三视图如图所示，如果小正方形 格的边长为1，那么该四面体最长棱的棱长为（ ）‎ A. B. C. 6 D. ‎ ‎【答案】C ‎ ‎ 且该三棱锥是放在棱长为的正方体中，所以，在三棱锥中，最长的棱长为 ‎，且，故选C. ‎ 热点二：证明或判断空间平行、垂直关系 ‎[4]空间平行问题的转化关系 平行问题的核心是线线平行，证明线线平行的常用方法有：三角形的中位线、平行线分线段成比例(三角形相似)、平行四边形等．‎ ‎[5] 空间垂直问题的转化关系 垂直问题的核心是线线垂直，证明线线垂直的常用方法有：‎ 等腰三角形底边上的中线、勾股定理、平面几何方法等．‎ ‎5．已知是不同的直线， 是不重合的平面，给出下面四个命题：‎ ‎①若，则 ‎②若，则 ‎③若是两条异面直线，若，则 ‎④如果，那么 上面命题中，正确的序号为（ ）‎ A. ①② B. ①③ C. ③④ D. ②③④[ : *xx* ]‎ ‎【答案】C 对于④，如果m⊥α，m垂直平面α内及与α平行的直线，故m⊥n，故正确；‎ 本题选择C选项. * ‎ ‎6．【浙江省湖州、衢州、丽水三市2017届高三4月联考】已知平面与两条不重合的直线，，则“，且”是“”的( )‎ A. 充分不必要条件 B. 必要不充分条件 C. 充分必要条件 D. 既不充分也不必要条件 ‎【答案】A ‎7．【贵州省凯里市第一中 2018届高三下 期《黄金卷》第三套模拟】若，表示空间中两条不重合的直线，，表示空间中两个不重合的平面，则下列命题中正确的是（ ）‎ A. 若，，则 B. 若，，，则 C. 若，，，则 D. 若，，，则 ‎【答案】C ‎【解析】对于，还可能有，故错；‎ 对于B ，还可能有异面，故B 错；C 正确；‎ 对于，还有平行、异面、相交，故错．‎ 故选：．‎ ‎8．【广东省肇庆市2018届高三第三次模拟】已知，，，四点均在以点为球心的球面上，且，，.若球在球内且与平面相切，则球直径的最大值为[ : XX ]‎ A. 1 B. 2 C. 4 D. 8‎ ‎【答案】D ‎【解析】如图所示:‎ ‎9.在四棱锥中， 平面， ， ，且， 为线段上一点．　‎ ‎（Ⅰ）求证：平面平面；‎ ‎（Ⅱ）若，求证： 平面．‎ ‎【答案】（Ⅰ）见解析;　（Ⅱ）见解析.‎ ‎【解析】试题分析：（1）要证平面平面，只需证明平面，而，所以只需证明，因为平面，所以成立，（2）在上取一点，使得，易得四边形为平行四边形，即有，再根据线面平行判定定理可得平面．‎ 试题解析：证明：（Ⅰ）因为平面， 平面， ‎ 所以，又，且，所以平面．‎ 因为平面，所以平面平面．　‎ ‎ ‎ ‎10.【江苏省2018年高考冲刺预测卷一】如图所示的多面体中，底面为正方形，为等边三角形，平面，，点是线段上除两端点外的一点，若点为线段的中点.‎ ‎（Ⅰ）求证：平面；‎ ‎（Ⅱ）求证：平面平面.‎ ‎【答案】（Ⅰ）见解析.（Ⅱ）见解析.‎ ‎【解析】试题分析：由点为线段的中点，故，由平面，得，得证平面，，平面，结合(1)的结果证得平面平面 热点三：空间角的求法 ‎[6]借助空间向量求空间角，是高考每年必考的重点和热点之一，对于异面直线所成的角：设两条异面直线的方向向量为，其夹角为，则 (其中为异面直线所成的角)，对于直线和平面所成的角：设直线的方向向量为，平面的法向量为，直线与平面所成的角为，两向量与的夹角为，则有，对于二面角：分别求出二面角的两个面所在平面的法向量，然后通过两个平面的法向量的夹角得到二面角的大小，但要注意结合实际图形判断所求角是锐角还是钝角．‎ ‎[7]求平面的法向量的方法 ‎(1)性质法：根据线面垂直的判定找出与平面垂直的直线，则此直线的方向向量就是平面的法向量．‎ ‎(2)赋值法：在平面内取两个不共线向量，设出平面的法向量建立方程组，通过赋值求出其中的一个法向量．‎ ‎11.【湖北省荆州市2018届高三质量检查（III）】如图，在直三棱柱中，，，点为棱的中点，点为线段上一动点.‎ ‎（Ⅰ）求证：当点为线段的中点时，平面；‎ ‎（Ⅱ）设，试问：是否存在实数，使得平面与平面所成锐二面角的余弦值为？若存在，求出这个实数；若不存在，请说明理由.‎ ‎【答案】（Ⅰ）见解析；（2）或 ‎【解析】试题分析：‎ ‎（Ⅰ）连、，由题意可证得．又在平面，从而可得平面．（Ⅱ）由题意可建立空间直角坐标系，结合条件可得，从而可得平面的法向量，同理可得平面的法向量，根据解得或，故存在实数满足条件． ‎ ‎（Ⅱ）解：以为原点，分别以、、为轴、轴、轴建立空间直角坐标系，‎ 连接、，设，‎ ‎∵，‎ ‎∴，‎ ‎∴，∴.‎ ‎∵点在线段上运动，‎ ‎∴平面的法向量即为平面的法向量，‎ 点睛：空间向量的引入为解决立体几何中的探索性问题提供了有力的工具．解决与平行、垂直有关的探索性问题时，通常假定题中的数 对象存在(或结论成立)，然后在这个前提下进行逻辑推理，若能导出与条件吻合的数据或事实，说明假设成立，即存在，并可进一步证明；若导出与条件或实际情况相矛盾的结果，则说明假设不成立，即不存在．‎ ‎12.【2017届湖南省衡阳市高三下第二次联考】如图，在四棱锥中， 平面，平面平面， ， 为等腰直角三角形， .‎ ‎（1）证明：平面平面；‎ ‎（2）若三棱锥的体积为，求平面与平面所成二面角的余弦值.‎ ‎【答案】（1）详见解析（2）‎ ‎【解析】试题分析：（1）证明面面垂直，通过证明线面垂直即可，根据 面，结合题目条件即可得平面，（2）由（1）面，所以AB为几何体高，所以 ，然后建立空间直接坐标系，写出两个平面得法向量，利用向量夹角公式求解即可。 ‎ 由（1）易知平面的一法向量为，设平面的法向量为.‎ ‎， .‎ ‎ ，取， .‎ ‎ ，故所求二面角的余弦值为.‎ ‎[ : _xx_ ]‎ ‎13.【四川省雅安市2018届高三下 期三诊】如图，在四棱锥中，底面，为的中点，底面为直角梯形，，，且.‎ ‎（1）求证：平面，平面平面；‎ ‎（2）若与平面所成角的正弦值为，求二面角的余弦值.‎ ‎【答案】（Ⅰ）见解析；（Ⅱ）.‎ 试题解析：（1）证明：设中点是，连接则，‎ ‎，‎ 为平行四边形，‎ ‎，‎ 平面，平面，‎ 平面，‎ 为直角梯形，，，且.‎ ‎，‎ ‎，‎ ‎ 底面 底面 ‎ 底面 平面平面. ‎ ‎ ‎ 平面的法向量，平面的法向量，‎ ‎.‎ 二面角的余弦值为.‎ 点睛：此题主要考查立体几何中线面直线及面面垂直的证明，二面角的三角函数值的求解，以及坐标法在解决立体几何问题中的应用等有关方面的知识和技能，属于中档题型，也是常考题型.坐标法在解决立体几何中的一般步骤，一是根据图形特点，建立空间直角坐标系；二是将几何中的量转化为向量，通过向量的运算；三是将运算得到的结果翻译为几何结论.‎