【数学】2019届一轮复习人教A版　集合的概念与运算学案

【数学】2019届一轮复习人教A版　集合的概念与运算学案

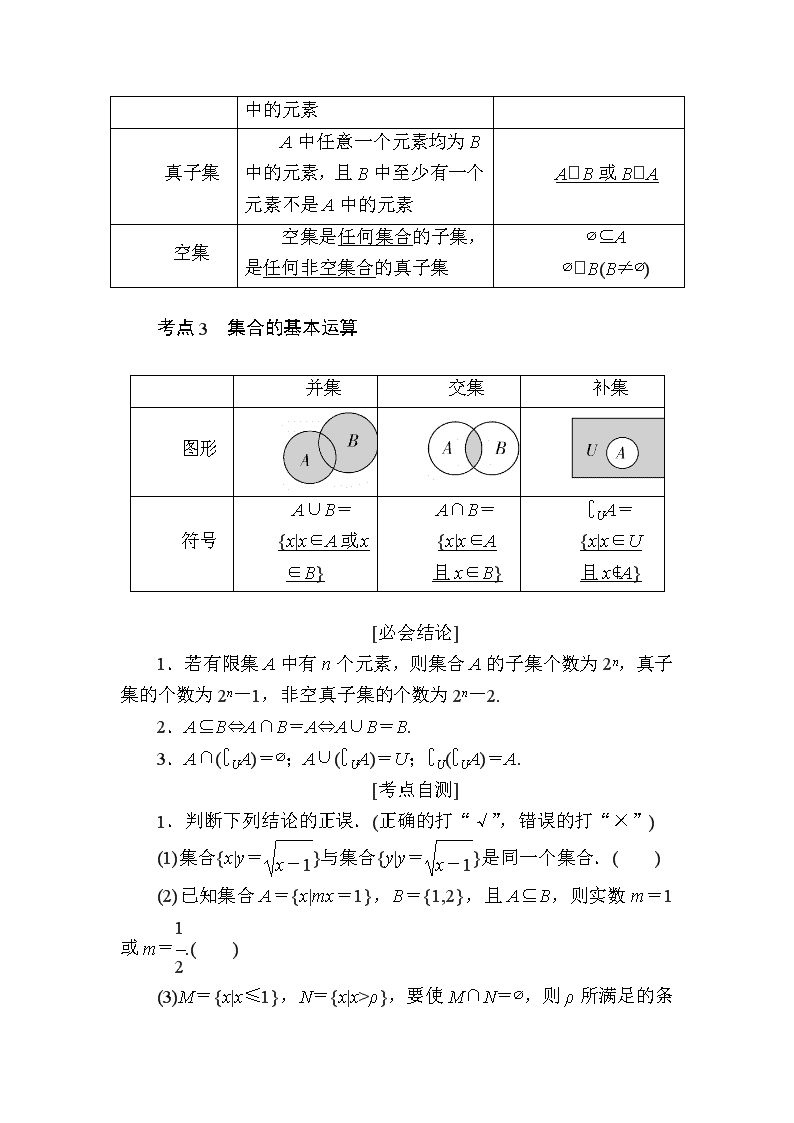
第1章　集合与常用逻辑用语 第1讲　集合的概念与运算 板块一　知识梳理·自主学习 ‎[必备知识]‎ 考点1　集合与元素 ‎1．集合中元素的三个特征：确定性、互异性、无序性．‎ ‎2．元素与集合的关系是属于或不属于两种，用符号∈或∉表示．‎ ‎3．集合的表示法：列举法、描述法、图示法．‎ ‎4．常见数集的记法 集合 自然数集 正整数集 整数集 有理数集 实数集 符号 N N*(或N＋)‎ Z Q R 考点2　集合间的基本关系 表示 关系　　‎ 文字语言 符号语言 相等 集合A与集合B中的所有元素相同 A⊆B且B⊆A ‎⇔A＝B 子集 A中任意一个元素均为B A⊆B或B⊇A 中的元素 真子集 A中任意一个元素均为B中的元素，且B中至少有一个元素不是A中的元素 AB或BA 空集 空集是任何集合的子集，是任何非空集合的真子集 ‎∅⊆A ‎∅B(B≠∅)‎ 考点3　集合的基本运算 并集 交集 补集 图形 符号 A∪B＝‎ ‎{x|x∈A或x∈B}‎ A∩B＝‎ ‎{x|x∈A 且x∈B}‎ ‎∁UA＝‎ ‎{x|x∈U 且x∉A}‎ ‎[必会结论]‎ ‎1．若有限集A中有n个元素，则集合A的子集个数为2n，真子集的个数为2n－1，非空真子集的个数为2n－2.‎ ‎2．A⊆B⇔A∩B＝A⇔A∪B＝B.‎ ‎3．A∩(∁UA)＝∅；A∪(∁UA)＝U；∁U(∁UA)＝A.‎ ‎[考点自测]‎ ‎1．判断下列结论的正误．(正确的打“√”，错误的打“×”)‎ ‎(1)集合{x|y＝}与集合{y|y＝}是同一个集合．(　　)‎ ‎(2)已知集合A＝{x|mx＝1}，B＝{1,2}，且A⊆B，则实数m＝1 或m＝.(　　)‎ ‎(3)M＝{x|x≤1}，N＝{x|x>ρ}，要使M∩N＝∅，则ρ所满足的条件是ρ≥1.(　　)‎ ‎(4)若集合A＝{－1,1}，B＝{0,2}，则集合{z|z＝x＋y，x∈A，y∈B}中有4个元素．(　　)‎ ‎(5)若5∈{1，m＋2，m2＋4}，则m的取值集合为{1，－1,3}．(　　)‎ 答案　(1)×　(2)×　(3)√　(4)×　(5)×‎ ‎2．[2017·北京高考]若集合A＝{x|－2＜x＜1}，B＝{x|x＜－1或x＞3}，则A∩B＝(　　)‎ A．{x|－2＜x＜－1} B．{x|－2＜x＜3}‎ C．{x|－1＜x＜1} D．{x|1＜x＜3}‎ 答案　A 解析　∵A＝{x|－2＜x＜1}，B＝{x|x＜－1或x＞3}，‎ ‎∴A∩B＝{x|－2＜x＜－1}．故选A.‎ ‎3．[课本改编]已知集合A＝{x|x2－2x－3≤0}，B＝{x|01} D．A∩B＝∅‎ 答案　A 解析　∵B＝{x|3x＜1}，∴B＝{x|x＜0}．‎ 又A＝{x|x＜1}，∴A∩B＝{x|x＜0}，A∪B＝{x|x＜1}．‎ 故选A.‎ ‎5．[2018·重庆模拟]已知集合A＝{x∈N|πx<16}，B＝{x|x2－5x＋4<0}，则A∩(∁RB)的真子集的个数为(　　)‎ A．1 B．3 C．4 D．7‎ 答案　B 解析　因为A＝{x∈N|πx<16}＝{0,1,2}，B＝{x|x2－5x＋4<0}＝{x|17}，B＝{x|x<2m－1}，若B⊆A，则实数m的取值范围是________．‎ 答案　(－∞，－1]‎ 解析　由题意知2m－1≤－3，m≤－1，∴m的取值范围是(－∞，－1]．‎ ‎　本例中的B改为B＝{x|m＋1≤x≤2m－1}，其余不变，该如何求解？‎ 解　当B＝∅时，有m＋1>2m－1，则m<2.‎ 当B≠∅时，或 解得m>6.综上可知m的取值范围是(－∞，2)∪(6，＋∞)．‎ ‎　本例中的A改为A＝{x|－3≤x≤7}，B改为B＝{x|m＋1≤x≤2m－1}，又该如何求解？‎ 解　当B＝∅时，满足B⊆A，此时有m＋1>2m－1，即m<2；当B≠∅时，要使B⊆A，则有解得2≤m≤4.‎ 综上可知m的取值范围是(－∞，4]．‎ 触类旁通 根据两集合的关系求参数的方法 ‎(1)空集是任何集合的子集，在涉及集合关系时，必须优先考虑空集的情况，否则会造成漏解．‎ ‎(2)已知两个集合间的关系求参数时，关键是将条件转化为元素或区间端点间的关系，进而转化为参数所满足的关系，常用数轴、Venn图等来直观解决这类问题．‎ ‎【变式训练2】　设A＝{x|x2－8x＋15＝0}，B＝{x|ax－1＝0}．‎ ‎(1)若a＝，试判定集合A与B的关系；‎ ‎(2)若BA，求实数a组成的集合C.‎ 解　(1)由x2－8x＋15＝0，‎ 得x＝3或x＝5，∴A＝{3,5}．‎ 若a＝，由ax－1＝0，得x－1＝0，即x＝5.‎ ‎∴B＝{5}．∴BA.‎ ‎(2)∵A＝{3,5}，又BA，‎ 故若B＝∅，则方程ax－1＝0无解，有a＝0；‎ 若B≠∅，则a≠0，由ax－1＝0，得x＝.‎ ‎∴＝3或＝5，即a＝或a＝.‎ 故C＝.‎ 考向　集合的基本运算 命题角度1　集合的交集及运算 例　3　[2017·山东高考]设集合M＝{x||x－1|<1}，N＝{x|x<2}，则M∩N＝(　　)‎ A．(－1,1) B．(－1,2)‎ C．(0,2) D．(1,2)‎ 答案　C 解析　∵M＝{x|00}，B＝{y|y＝ex＋1}，则A∪B等于(　　)‎ A．{x|x<2} B．{x|11} D．{x|x>0}‎ 答案　D 解析　由2x－x2>0得01，故B＝{y|y>1}，所以A∪B＝{x|x>0}．故选D.‎ 命题角度3　集合的补集及运算 例　5　[2016·浙江高考]已知集合P＝{x∈R|1≤x≤3}，Q＝{x∈R|x2≥4}，则P∪(∁RQ)＝(　　)‎ A．[2,3] B．(－2,3]‎ C．[1,2) D．(－∞，－2]∪[1，＋∞)‎ 答案　B 解析　∵Q＝(－∞，－2]∪[2，＋∞)，∴∁RQ＝(－2,2)，∴P∪(∁RQ)＝(－2,3]．故选B.‎ 命题角度4　抽象集合的运算 例　6　[2018·唐山统一测试]若全集U＝R，集合A＝，B＝{x|2x<1}，则下图中阴影部分表示的集合是(　　)‎ A．{x|2－1.‎ ‎9．[2018·郑州模拟]已知集合A＝{x∈R||x＋2|<3}，集合B＝，且A∩B＝(－1，n)，则m＝________，n＝________.‎ 答案　－1　1‎ 解析　A＝{x∈R||x＋2|<3}＝{x∈R|－50或y＝－1，－2}，(∁RA)∩B＝{－1，－2}．所以D正确．‎ ‎2．[2018·湖南模拟]设常数a∈R，集合A＝{x|(x－1)(x－a)≥0}，B＝{x|x≥a－1}，若A∪B＝R，则a的取值范围为(　　)‎ A．(－∞，2) B．(－∞，2]‎ C．(2，＋∞) D．[2，＋∞)‎ 答案　B 解析　集合A讨论后利用数轴可知或 解得1≤a≤2或a≤1，即a≤2.故选B.‎ ‎3．已知数集A＝{a1，a2，…，an}(1≤a17}．‎ 又Q＝{x|x2－3x－10≤0}＝{x|－2≤x≤5}，所以(∁RP)∩Q＝{x|x<4或x>7}∩{x|－2≤x≤5}＝{x|－2≤x＜4}．‎ ‎(2)当P≠∅时，由P∪Q＝Q得P⊆Q，‎ 所以解得0≤a≤2；‎ 当P＝∅，即2a＋1

查看更多