【数学】2019届一轮复习人教A版（文）集合的概念与运算学案

【数学】2019届一轮复习人教A版（文）集合的概念与运算学案

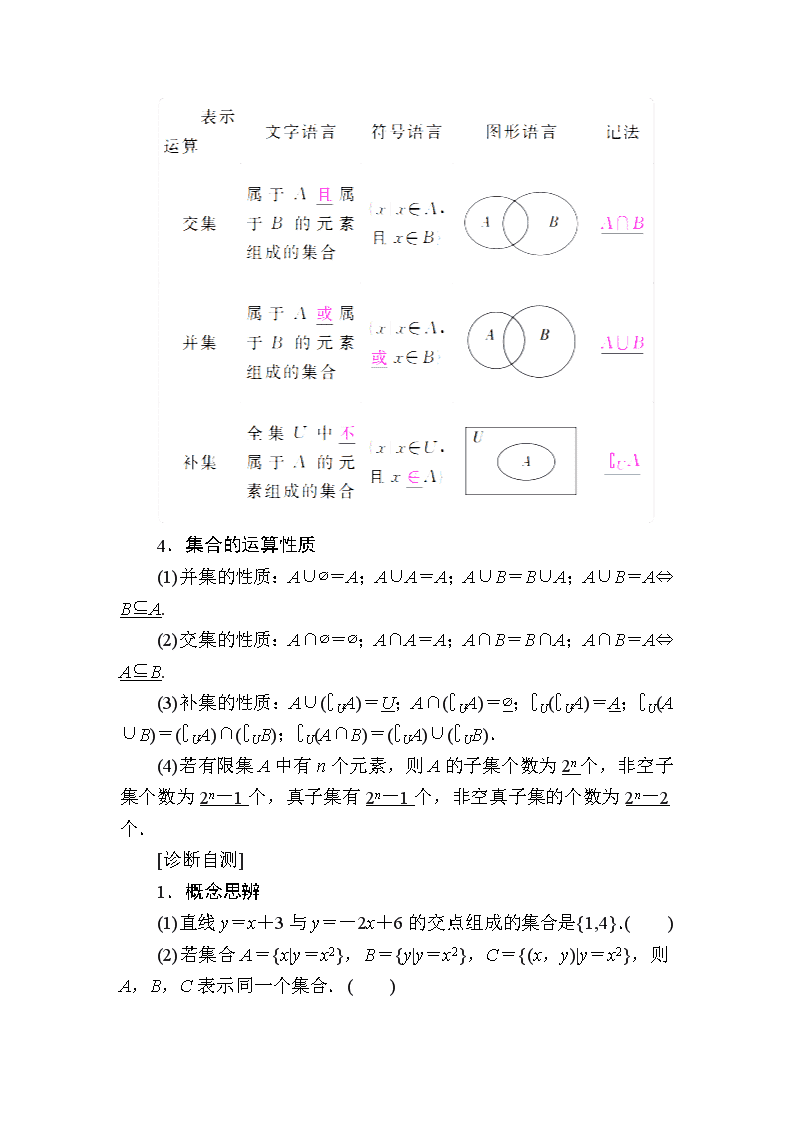
‎1．1　集合的概念与运算 ‎[知识梳理]‎ ‎1．集合与元素 ‎(1)集合中元素的三个特征：确定性、互异性、无序性．‎ ‎(2)元素与集合的关系有属于或不属于两种，用符号∈或∉表示．‎ ‎(3)集合的表示法：列举法、描述法、图示法．‎ ‎(4)常见数集的记法 集合 自然数集 正整数集 整数集 有理数集 实数集 符号 N N*(或N＋)‎ Z Q R ‎2．集合间的基本关系 ‎3．集合的基本运算 ‎4．集合的运算性质 ‎(1)并集的性质：A∪∅＝A；A∪A＝A；A∪B＝B∪A；A∪B＝A⇔B⊆A.‎ ‎(2)交集的性质：A∩∅＝∅；A∩A＝A；A∩B＝B∩A；A∩B＝A⇔A⊆B.‎ ‎(3)补集的性质：A∪(∁UA)＝U；A∩(∁UA)＝∅；∁U(∁UA)＝A；∁U(A∪B)＝(∁UA)∩(∁UB)；∁U(A∩B)＝(∁UA)∪(∁UB)．‎ ‎(4)若有限集A中有n个元素，则A的子集个数为2n个，非空子集个数为2n－1个，真子集有2n－1个，非空真子集的个数为2n－2个．‎ ‎[诊断自测]‎ ‎1．概念思辨 ‎(1)直线y＝x＋3与y＝－2x＋6的交点组成的集合是{1,4}．(　　)‎ ‎(2)若集合A＝{x|y＝x2}，B＝{y|y＝x2}，C＝{(x，y)|y＝x2}，则A，B，C表示同一个集合．(　　)‎ ‎(3)设集合A＝{0,1}，若B＝{x|x⊆A}，则A⊆B.(　　)‎ ‎(4)设集合A＝{x|ax＝1}，B＝{x|x2＝1}，若A⊆B，则a＝1或－1.(　　)‎ 答案　(1)×　(2)×　(3)×　(4)×‎ ‎2．教材衍化 ‎(1)(必修A1P12T10)若集合P＝{x|x≥5}，Q＝{x|5≤x≤7}，则P与Q的关系是(　　)‎ A．P＝Q B．PQ C．PQ D．P⊄Q 答案　C 解析　因为集合P＝{x|x≥5}，Q＝{x|5≤x≤7}，所以QP.故选C.‎ ‎(2)(必修A1P12T2)已知A＝{(x，y)|4x＋y＝6}，B＝{(x，y)|3x＋2y＝7}，则A∩B＝________.‎ 答案　{(1,2)}‎ 解析　A∩B＝{(x，y)|4x＋y＝6}∩{(x，y)|3x＋2y＝7}＝＝{(1,2)}．‎ ‎3．小题热身 ‎(1)已知集合A＝{x|－37}，B＝{x|x<2m－1}，若B⊆A，则实数m的取值范围是________．‎ 本题可结合数轴用数形结合方法．‎ 答案　(－∞，－1]‎ 解析　由题意知2m－1≤－3，m≤－1，∴m的取值范围是(－∞，－1]．‎ ‎[条件探究1]　典例2中的B改为B＝{x|m＋1≤x≤2m－1}，其余不变，该如何求解？‎ 解　当B＝∅时，有m＋1>2m－1，则m<2；‎ 当B≠∅时，或 解得m>6.综上可知m的取值范围是(－∞，2)∪(6，＋∞)．‎ ‎[条件探究2]　典例2中的A改为A＝{x|－3≤x≤7}，B改为B＝{x|m＋1≤x≤2m－1}，又该如何求解？‎ 解　当B＝∅时，满足B⊆A，此时有m＋1>2m－1，‎ 即m<2；当B≠∅，要使B⊆A，则有 解得2≤m≤4.‎ 综上可知m的取值范围是(－∞，4]．‎ 方法技巧 ‎1．集合相等的问题求解思路 首先分析已知元素与另一个集合中的哪个元素相等，一般要分类讨论，列出方程(组)求解，最后要验证是否满足互异性．例如典例1.‎ ‎2．已知两个集合间的关系求参数时的关键点及注意点 ‎(1)关键点：将条件转化为元素或区间端点间的关系，进而转化为参数所满足的关系．‎ ‎(2)注意点：①利用数轴、Venn图帮助分析及对参数进行讨论；②注意区间端点的取舍．例如典例2.‎ 提醒：空集是任何集合的子集，在涉及集合关系时，必须优先考虑空集的情况，否则会造成漏解．‎ 冲关针对训练　‎ ‎1．已知集合A＝{x|x2－2x>0}，B＝{x|－2或x<0}，又B＝{x|－0}，则A∩B＝(　　)‎ A. B. C. D. 本题用转化法，数形结合法．‎ 答案　D 解析　易知A＝(1,3)，B＝，∴A∩B＝.故选D.‎ 角度2　求并集 (2018·浙江模拟)已知集合P＝{x|－10}，B＝{x|y＝lg (x－1)}，则(∁UA)∩B＝(　　)‎ A．{x|x>2或x<0} B．{x|10，即x(x－2)>0，得x<0或x>2，故A＝{x|x<0或x>2}．集合B是函数y＝lg (x－1)的定义域，由x－1>0，解得x>1，所以B＝{x|x>1}．易知∁UA＝{x|0≤x≤2}，所以(∁UA)∩B＝{x|0≤x≤2}∩{x|x>1}＝{x|10}，则(　　)‎ A．A∩B＝ B．A∩B＝∅‎ C．A∪B＝ D．A∪B＝R 答案　A 解析　由3－2x>0得x<，则B＝，所以A∩B＝.故选A.‎ ‎2．(2017·全国卷Ⅲ)已知集合A＝{(x，y)│x2＋y2＝1}，B＝{(x，y)│y＝x}，则A∩B中元素的个数为(　　)‎ A．3 B．2‎ C．1 D．0‎ 答案　B 解析　集合A表示以原点O为圆心，半径为1的圆上的所有点的集合，集合B表示直线y＝x上的所有点的集合．‎ 由图形可知，直线与圆有两个交点，‎ 所以A∩B中元素的个数为2.故选B.‎ ‎3．(2018·武昌调研)设A，B是两个非空集合，定义集合A－B＝{x|x∈A，且x∉B}．若A＝{x∈N|0≤x≤5}，B＝{x|x2－7x＋10<0}，则A－B＝(　　)‎ A．{0,1} B．{1,2}‎ C．{0,1,2} D．{0,1,2,5}‎ 答案　D 解析　A＝{0,1,2,3,4,5}，B＝{x|21}，则(∁RA)∩B＝(　　)‎ A．[1，＋∞) B．(0，＋∞)‎ C．(0,1) D．[0,1]‎ 答案　A 解析　依题意得，A＝{x|00}，故(∁RA)∩B＝{x|x≥1}＝[1，＋∞)．故选A.‎ ‎5．若集合M＝{x||x|≤1}，N＝{y|y＝x2，|x|≤1}，则(　　)‎ A．M＝N B．M⊆N C．N⊆M D．M∩N＝∅‎ 答案　C 解析　M＝{x||x|≤1}＝[－1,1]，N＝{y|y＝x2，|x|≤1}＝[0,1]，所以N⊆M.故选C.‎ ‎6．(2017·山西模拟)设全集U＝R，集合A＝{x∈N|x2<6x}，B＝{x∈N|30可解得－60}，集合B＝{x|x2－2ax－1≤0，a>0}，若A∩B中恰含有一个整数，则实数a的取值范围是(　　)‎ A. B． C. D．(1，＋∞)‎ 答案　B 解析　A＝{x|x2＋2x－3>0}＝{x|x>1或x<－3}，‎ 设函数f(x)＝x2－2ax－1，因为函数f(x)＝x2－2ax－1图象的对称轴为x＝a(a>0)，f(0)＝－1<0，根据对称性可知若A∩B中恰有一个整数，则这个整数为2，‎ 所以有即 所以即≤a<.故选B.‎ 二、填空题 ‎11．(2017·南昌模拟)已知集合M＝{x|x2－4x<0}，N＝{x|m－2时，B＝(m－1,2m＋1)，因此，要B⊆A，‎ 则只要⇒－1≤m≤2.‎ 综上所述，m的取值范围是{m|m＝－2或－1≤m≤2}．‎