2019届二轮复习第十三章数系的扩充与复数的引入课件（8张）（全国通用）

2019届二轮复习第十三章数系的扩充与复数的引入课件（8张）（全国通用）

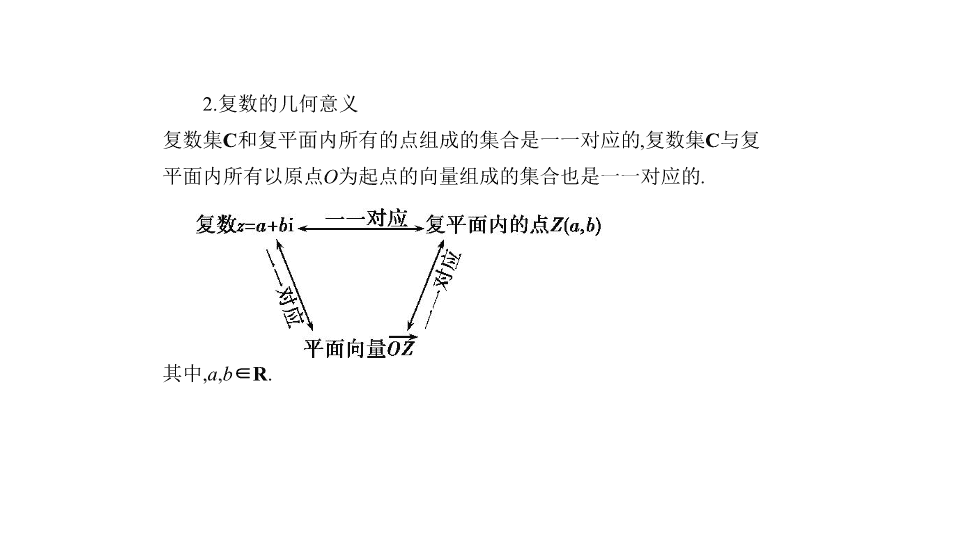
考点一    复数的概念与几何意义 考向基础 1.复数的有关概念 考点清单 　　2.复数的几何意义 复数集 C 和复平面内所有的点组成的集合是一一对应的,复数集 C 与复 平面内所有以原点 O 为起点的向量组成的集合也是一一对应的.   其中, a , b ∈ R . 例1     (2018河南开封定位考试,2)复数 z =   (其中i是虚数单位),则   (　　) A. z 的共轭复数为-1-i　　B. z 的实部为1 C.| z |=2　     D. z 的虚部为-1 考向突破 考向    复数的有关概念 解析      z =   =   =-1-i,∴   =-1+i,故A错; z 的实部为-1,故B 错;| z |=   ,故C错; z 的虚部为-1,故D正确. 答案     D 考点二    复数代数形式的四则运算 考向基础 1.复数的加、减、乘、除运算法则 设 z 1 = a + b i, z 2 = c + d i( a , b , c , d ∈ R ),则 (1)加法: z 1 + z 2 =( a + b i)+( c + d i)=( a + c )+( b + d )i; (2)减法: z 1 - z 2 =( a + b i)-( c + d i)=( a - c )+( b - d )i; (3)乘法: z 1 · z 2 =( a + b i)·( c + d i)=( ac - bd )+( ad + bc )i; (4)除法:   =   =   =   ( c + d i ≠ 0). 2.复数加法的运算律 复数的加法满足交换律、结合律,即对任何 z 1 、 z 2 、 z 3 ∈ C ,有 z 1 + z 2 = z 2 + z 1 , ( z 1 + z 2 )+ z 3 = z 1 +( z 2 + z 3 ). 例2     (2018豫南九校第六次质量考评,2)已知复数   = x + y i( a , x , y ∈ R ,i 是虚数单位),则 x +2 y =   (　　) A.1　    B.   　    C.-   　    D.-1 考向突破 考向    复数的四则运算 解析 　由题意得 a +i=( x + y i)(2+i)=2 x - y +( x +2 y )i, ∴ x +2 y =1,故选A. 答案     A 方法    复数代数形式的四则运算方法 复数的四则运算中,加减法相当于“合并同类项”,乘法相当于“多项 式乘多项式”,除法采用的方法是 “分母实数化” ,即分子、分母同乘 分母的共轭复数,类似于“分母有理化”的方法,可类比记忆.此外,一要 注意出现i 2 时用-1代替,二要注意“复数问题实数化”是解决复数问题 的最基本的思想方法. 方法技巧 例     (2017湖北黄石调研,3)若复数 z 满足 z (2+i)=   (i为虚数单位),则 z 的 共轭复数   =   (　　) A.1+3i　　B.1-3i C.3+i　　D.3-i 解题导引 解析      z (2+i)=   ⇒ z =   =   =1-3i ⇒   =1+3i.故选A. 答案     A