2019届二轮复习（理）客观题提速练四作业（全国通用）

2019届二轮复习（理）客观题提速练四作业（全国通用）

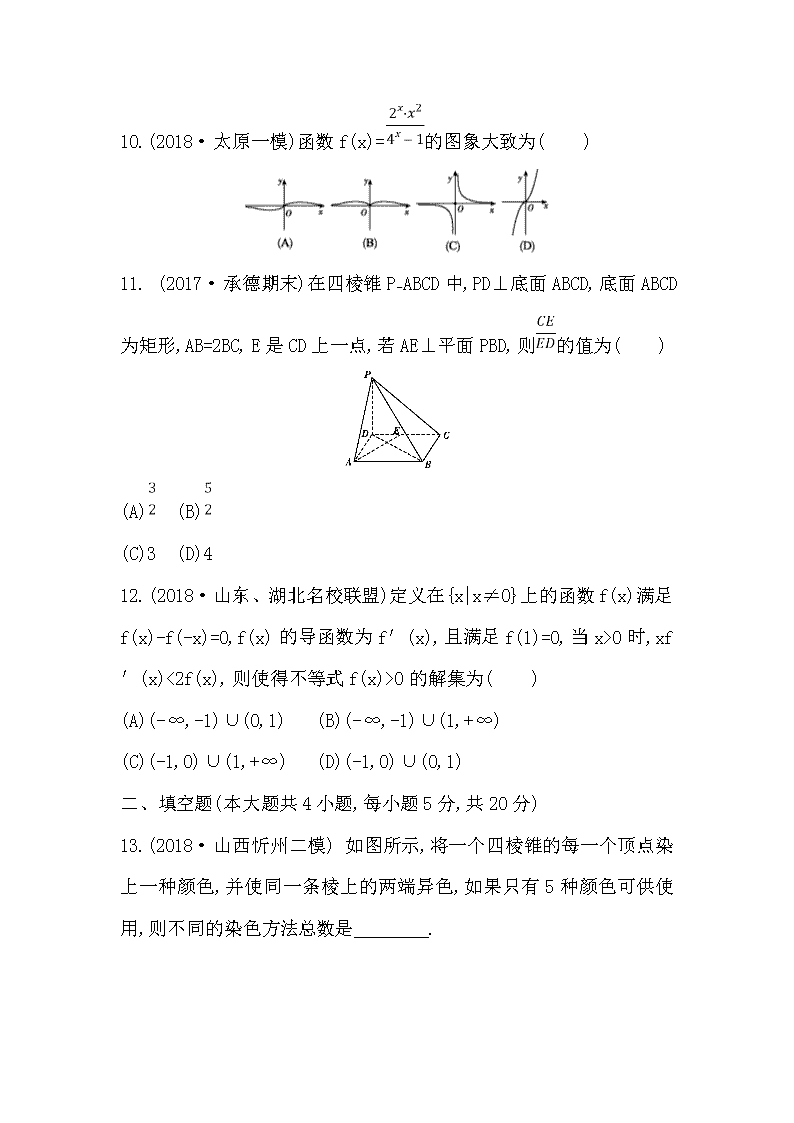
客观题提速练四 ‎(时间:45分钟　满分:80分)‎ 一、选择题(本大题共12小题,每小题5分,共60分)‎ ‎1.(2018·吉林省实验中学模拟)已知N是自然数集,集合A=｛x︱∈N｝,B={0,1,2,3,4},则A∩B等于(　　)‎ ‎(A){0,2} (B){0,1,2} (C){2,3} (D){0,2,4}‎ ‎2.已知条件p:t=,q:sin xdx=1,则p是q的(　　)‎ ‎(A)充分不必要条件 (B)必要不充分条件 ‎(C)充分必要条件 (D)既不充分也不必要条件 ‎3.(2018·石家庄一模)已知f(x)为偶函数,且当x∈[0,2)时,f(x)=2sin x,当x∈[2,+∞)时,f(x)=log2x,则f（-）+f(4)等于(　　)‎ ‎(A)-+2 (B)1‎ ‎(C)3 (D)+2‎ ‎4.(2018·河北邢台质检)过抛物线的焦点F的直线,交抛物线于A,B两点,交准线于C点,若=2,=λ·,则实数λ等于(　　)‎ ‎(A)-4 (B)4 (C)2 (D)-2‎ ‎5.(2018·全国Ⅰ卷)已知函数f(x)=2cos2x-sin2x+2,则(　　)‎ ‎(A)f(x)的最小正周期为π,最大值为3‎ ‎(B)f(x)的最小正周期为π,最大值为4‎ ‎(C)f(x)的最小正周期为2π,最大值为3‎ ‎(D)f(x)的最小正周期为2π,最大值为4‎ ‎6.(2018·东北三省四市教研联合体一模)已知边长为2的等边三角形ABC,D为BC的中点,以AD为折痕,将△ABC折成直二面角B-AD-C,则过A,B,C,D四点的球的表面积为(　　)‎ ‎(A)3π (B)4π (C)5π (D)6π ‎7.(2017·衡水金卷二模)若点P是以F1,F2为焦点的双曲线x2-= 1(b>0)上一点,PF1⊥PF2,且|PF1|=2|PF2|,则此双曲线的标准方程是(　　)‎ ‎(A)x2-=1 (B)x2-=1‎ ‎(C)x2-=1 (D)x2-=1‎ ‎8.(2018·南充三模)表中提供了某厂节能降耗技术改造后生产A产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对应数据.根据下表提供的数据,求出y关于x的线性回归方程为=0.7x+0.35,那么表中t的值为(　　)‎ x ‎3‎ ‎4‎ ‎5‎ ‎6‎ y ‎2.5‎ t ‎4‎ ‎4.5‎ ‎(A)3 (B)3.15 (C)3.5 (D)4.5‎ ‎9.(2018·陕西渭南二模)已知数列{xn}满足xn+2=|xn+1-xn|(n∈N*),若x1=1,x2=a(a≤1,a≠0),且xn+3=xn对于任意的正整数n均成立,则数列{xn}的前2 019项和S2 019等于(　　)‎ ‎(A)673 (B)674 (C)1 344 (D)1 346‎ ‎10.(2018·太原一模)函数f(x)=的图象大致为(　　)‎ ‎11. (2017·承德期末)在四棱锥PABCD中,PD⊥底面ABCD,底面ABCD为矩形,AB=2BC,E是CD上一点,若AE⊥平面PBD,则的值为(　　)‎ ‎(A) (B)‎ ‎(C)3 (D)4‎ ‎12. (2018·山东、湖北名校联盟)定义在{x|x≠0}上的函数f(x)满足f(x)-f(-x)=0,f(x)的导函数为f′(x),且满足f(1)=0,当x>0时,xf′(x)<‎2f(x),则使得不等式f(x)>0的解集为(　　)‎ ‎(A)(-∞,-1)∪(0,1) (B)(-∞,-1)∪(1,+∞)‎ ‎(C)(-1,0)∪(1,+∞) (D)(-1,0)∪(0,1)‎ 二、填空题(本大题共4小题,每小题5分,共20分)‎ ‎13.(2018·山西忻州二模) 如图所示,将一个四棱锥的每一个顶点染上一种颜色,并使同一条棱上的两端异色,如果只有5种颜色可供使用,则不同的染色方法总数是　　　　. ‎ ‎14. (2018·济南调研)为了研究某药品的疗效,选取若干名志愿者进行临床试验.所有志愿者的舒张压数据(单位:kPa)的分组区间为[12, 13),[13,14),[14,15),[15,16),[16,17],将其按从左到右的顺序分别编号为第一组,第二组,……,第五组.如图是根据试验数据制成的频率分布直方图.已知第一组与第二组共有20人,第三组中没有疗效的有6人,则第三组中有疗效的人数为　　　　. ‎ ‎15.(2018·山东、湖北部分重点中学模拟)设实数x,y满足则的最小值是　　　　. ‎ ‎16.(2018·上高模拟)定义在实数集R上的函数f(x),如果存在函数g(x)=Ax+B(A,B为常数),使得f(x)≥g(x)对一切实数x都成立,那么称g(x)为函数f(x)的一个承托函数.给出如下四个结论:‎ ‎①对于给定的函数f(x),其承托函数可能不存在,也可能有无数个;‎ ‎②定义域和值域都是R的函数f(x)不存在承托函数;‎ ‎③g(x)=2x为函数f(x)=|3x|的一个承托函数;‎ ‎④g(x)=x为函数f(x)=x2的一个承托函数.‎ 其中所有正确结论的序号是　　　　　　　　. ‎ ‎1.B　因为A=｛x︱∈N｝={0,1,2,5},B={0,1,2,3,4},‎ 所以A∩B={0,1,2}.故选B.‎ ‎2.A　由sin xdx=(-cos x) ︱=-cos t+1=1得cos t=0,所以t=+kπ(k∈N),于是p是q的充分不必要条件.故选A.‎ ‎3.D　因为f（-）=f（）=2sin =,f(4)=log24=2,所以f（-）+f(4)=+2.‎ ‎4.A　过点A,B分别作抛物线准线的垂线,垂足为M,N,设BF=m,则AF=AM=‎2m,BN=m,由△CBN∽△CAM,得=,=,则CB=‎3m,又,方向相反,则λ=-= -= -4,故选A.‎ ‎5.B　因为f(x)=2cos2x-sin2x+2=1+cos 2x-+2=cos 2x+,所以f(x)的最小正周期为π,最大值为4.故选B.‎ ‎6.C　如图所示.‎ 边长为2的等边三角形ABC,D为BC的中点,以AD为折痕,将△‎ ABC折成直二面角B-AD-C,则AD=,BD=CD=1,设球的半径为r,则(2r)2=1+1+3=5,解得r2=,所以S=‎ ‎4πr2=4π·=5π,故选C.‎ ‎7.A　因为|PF1|=2|PF2|,|PF1|-|PF2|=‎2a,所以|PF1|=‎4a,|PF2|=‎2a,因为PF1⊥PF2, |F‎1F2|=‎2c,所以|PF1|2+|PF2|2=|F‎1F2|2,所以c2=‎5a2,因为a=1,所以c2=5,b2=4,故双曲线的方程为x2-=1.故选A.‎ ‎8.A　因为==4.5,=,因为(,)满足回归方程,所以=0.7×4.5+0.35,解得t=3,故选A.‎ ‎9.D　因为x1=1,x2=a(a≤1,a≠0),所以x3=|x2-x1|=|a-1|=1-a,所以x1+x2+x3=1+a+ (1-a)=2,又xn+3=xn对于任意的正整数n均成立,所以数列{xn}的周期为3,所以数列{xn}的前2 019项和S2 019=S673×3=673×2=1 346,故选D.‎ ‎10.A　函数f(x)=的定义域为(-∞,0)∪(0,+∞),所以f(-x)= == -f(x),所以函数f(x)为奇函数,故排除B,因为f(1)==,f(2)==,所以f(1)< f(2),故排除C,当x→+∞时,f(x)→0,故排除D,故选A.‎ ‎11.C　因为PD⊥底面ABCD,所以PD⊥AE,又AE⊥平面PBD,所以AE⊥BD,此时△ABD∽△DAE,则=,因为AB=2BC,所以DE=AB=CD,所以 ‎=3.故选C.‎ ‎12.D　当x>0时,xf′(x)<‎2f(x),令g(x)=,x>0时,g′(x)==<0,‎ 所以g(x)在(0,+∞)上递减,又g(x)为偶函数,且g(1)=0,所以g(x)>0时,-10时,-10的解集为(-1,0)∪(0,1).‎ 故选D.‎ ‎13.解析:按所用颜色种数分类:‎ 第一类:5种颜色全用,共有种不同的方法;‎ 第二类:只用4种颜色,则必有某两个顶点同色(A与C,或B与D),共有2×种不同的方法;‎ 第三类:只用3种颜色,则A与C,B与D必定同色,共有种不同的方法.‎ 由分类加法计算原理,得不同的染色方法总数为+2×+=420.‎ 答案:420‎ ‎14.解析:全体志愿者共有=50(人),所以第三组志愿者有0.36×1× 50=18(人),因为第三组中没有疗效的有6人,所以有疗效的有18-6=12(人).‎ 答案:12‎ ‎15.解析:不等式组对应的可行域如图,‎ 令u=1+,则u在点(3,1)处取得最小值,umin=1+=,在点(1,2)处取得最大值,umax=1+2=3,所以=（）=（）u的最小值为（）3=.‎ 答案:‎ ‎16.解析:由题意可知,如果存在函数g(x)=Ax+B(A,B为常数),使得f(x)≥g(x)对一切实数x都成立,那么称g(x)为函数f(x)的一个承托函数,那么对于f(x)=B来说,不存在承托函数,当f(x)=2x,g(x)=x,则此时有无数个承托函数;②定义域和值域都是R的函数f(x)不存在承托函数,因为一个函数本身就是自己的承托函数.故错误;对于③因为f(x)=|3x|≥2x恒成立,则可知g(x)=2x为函数f(x)=|3x|的一个承托函数;成立;对于④如果g(x)=x为函数f(x)=x2的一个承托函数.则必然有x2≥x并非对任意实数都成立,只有当x≥或x≤0时成立,因此错误;综上可知正确的序号为①③.‎ 答案:①③‎