人教A版数学必修二2-2-1直线与平面平行的判定

人教A版数学必修二2-2-1直线与平面平行的判定

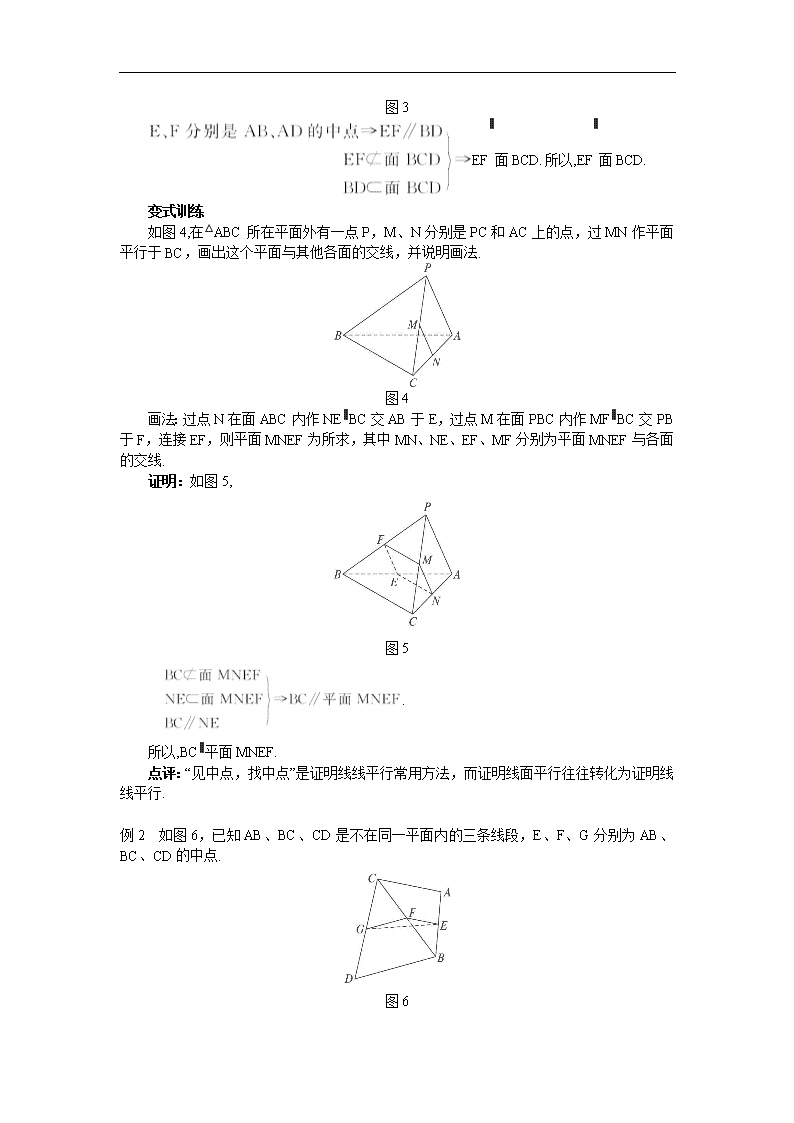
§2.2 直线、平面平行的判定及其性质 §2.2.1 直线与平面平行的判定 一、教材分析 空间里直线与平面之间的位置关系中，平行是一种非常重要的关系，它不仅应用较多， 而且是学习平面与平面平行的基础.空间中直线与平面平行的定义是以否定形式给出的用起 来不方便，要求学生在回忆直线与平面平行的定义的基础上探究直线与平面平行的判定定理. 本节重点是直线与平面平行的判定定理的应用. 二、教学目标 1．知识与技能 （1）理解并掌握直线与平面平行、平面与平面平行的判定定理； （2）进一步培养学生观察、发现的能力和空间想象能力； 2．过程与方法 学生通过观察图形，借助已有知识，掌握直线与平面平行、平面与平面平行的判定定理. 3．情感、态度与价值观 （1）让学生在发现中学习，增强学习的积极性； （2）让学生了解空间与平面互相转换的数学思想. 三、教学重点与难点 如何判定直线与平面平行. 四、课时安排 1 课时 五、教学设计 （一）复习 复习直线与平面平行的定义：如果直线与平面没有公共点叫做直线与平面平行. （二）导入新课 思路 1.(情境导入) 将一本书平放在桌面上，翻动书的封面，封面边缘 AB 所在直线与桌面所在平面具有什 么样的位置关系？ 思路 2.(事例导入) 观察长方体（图 1），你能发现长方体 ABCD—A′B′C′D′中，线段 A′B 所在的直线与长方 体 ABCD—A′B′C′D′的侧面 C′D′DC 所在平面的位置关系吗？ 图 1 （三）推进新课、新知探究、提出问题 ①回忆空间直线与平面的位置关系. ②若平面外一条直线平行平面内一条直线，探究平面外的直线与平面的位置关系. ③用三种语言描述直线与平面平行的判定定理. ④试证明直线与平面平行的判定定理. 活动：问题①引导学生回忆直线与平面的位置关系. 问题②借助模型锻炼学生的空间想象能力. 问题③引导学生进行语言转换. 问题④引导学生用反证法证明. 讨论结果：①直线在平面内、直线与平面相交、直线与平面平行. ②直线 a 在平面α外，是不是能够断定 a∥α呢？ 不能！直线 a 在平面α外包含两种情形：一是 a 与α相交，二是 a 与α平行， 因此，由直线 a 在平面α外，不能断定 a∥α. 若平面外一条直线平行平面内一条直线，那么平面外的直线与平面的位置关系可能相交 吗？ 既然不可能相交，则该直线与平面平行. ③直线与平面平行的判定定理： 平面外一条直线与此平面内的一条直线平行，那么该直线与此平面平行. 符号语言为： . 图形语言为：如图 2. 图 2 ④证明：∵a∥b，∴a、b 确定一个平面，设为β. ∴a  β，b  β. ∵a  α，a β，∴α和β是两个不同平面. ∵b  α且 b  β， ∴α∩β=b.假设 a 与α有公共点 P, 则 P∈α∩β=b，即点 P 是 a 与 b 的公共点，这与已知 a∥b 矛盾. ∴假设错误.故 a∥α. （四）应用示例 思路 1 例 1 求证空间四边形相邻两边中点的连线平行于经过另外两边的平面. 已知空间四边形 ABCD 中，E、F 分别是 AB、AD 的中点. 求证：EF∥面 BCD. 活动：先让学生思考或讨论，后再回答，经教师提示、点拨，对回答正确的学生及时表 扬，对回答不准确的学生提示引导考虑问题的思路. 证明：如图 3,连接 BD, 图 3 EF∥面 BCD.所以,EF∥面 BCD. 变式训练 如图 4,在△ABC 所在平面外有一点 P，M、N 分别是 PC 和 AC 上的点，过 MN 作平面 平行于 BC，画出这个平面与其他各面的交线，并说明画法. 图 4 画法：过点 N 在面 ABC 内作 NE∥BC 交 AB 于 E，过点 M 在面 PBC 内作 MF∥BC 交 PB 于 F，连接 EF，则平面 MNEF 为所求，其中 MN、NE、EF、MF 分别为平面 MNEF 与 各面的交线. 证明：如图 5, 图 5 . 所以,BC∥平面 MNEF. 点评：“见中点，找中点”是证明线线平行常用方法，而证明线面平行往往转化为证明线 线平行. 例 2 如图 6，已知 AB、BC、CD 是不在同一平面内的三条线段，E、F、G 分别为 AB、 BC、CD 的中点. 图 6 求证：AC∥平面 EFG，BD∥平面 EFG. 证明：连接 AC、BD、EF、FG、EG. 在△ABC 中， ∵E、F 分别是 AB、BC 的中点,∴AC∥EF. 又 EF  面 EFG，AC  面 EFG, ∴AC∥面 EFG. 同理可证 BD∥面 EFG. 变式训练 已知 M、N 分别是△ADB 和△ADC 的重心，A 点不在平面α内，B、D、C 在平面α内， 求证：MN∥α. 证明：如图 7,连接 AM、AN 并延长分别交 BD、CD 于 P、Q，连接 PQ. 图 7 ∵M、N 分别是△ADB、△ADC 的重心， ∴ NQ AN MP AM  =2.∴MN∥PQ. 又 PQ  α，MN  α,∴MN∥α. 点评：利用平面几何中的平行线截比例线段定理,三角形的中位线性质等知识促成“线线 平行”向“线面平行”的转化. 思路 2 例题 设 P、Q 是边长为 a 的正方体 AC1 的面 AA1D1D、面 A1B1C1D1 的中心,如图 8, （1）证明 PQ∥平面 AA1B1B； （2）求线段 PQ 的长. 图 8 (1)证法一：取 AA1,A1B1 的中点 M,N,连接 MN,NQ,MP, ∵MP∥AD,MP= AD2 1 ,NQ∥A1D1,NQ= 112 1 DA , ∴MP∥ND 且 MP=ND. ∴四边形 PQNM 为平行四边形. ∴PQ∥MN. ∵MN  面 AA1B1B,PQ  面 AA1B1B, ∴PQ∥面 AA1B1B. 证法二：连接 AD1,AB1,在△AB1D1 中,显然 P,Q 分别是 AD1,D1B1 的中点, ∴PQ∥AB1,且 PQ= 12 1 AB . ∵PQ  面 AA1B1B,AB1  面 AA1B1B, ∴PQ∥面 AA1B1B. (2)解:方法一:PQ=MN= aNAMA 2 22 1 2 1  . 方法二：PQ= aAB 2 2 2 1 1  . 变式训练 如图 9，正方体 ABCD—A1B1C1D1 中，E 在 AB1 上，F 在 BD 上，且 B1E=BF. 图 9 求证：EF∥平面 BB1C1C. 证明：连接 AF 并延长交 BC 于 M，连接 B1M. ∵AD∥BC,∴△AFD∽△MFB. ∴ BF DF FM AF  . 又∵BD=B1A，B1E=BF,∴DF=AE. ∴ BF DF FM AF  . ∴EF∥B1M，B1M  平面 BB1C1C. ∴EF∥平面 BB1C1C. （五）知能训练 已知四棱锥 P—ABCD 的底面为平行四边形,M 为 PC 的中点,求证:PA∥平面 MBD. 证明：如图 10,连接 AC、BD 交于 O 点,连接 MO, 图 10 ∵O 为 AC 的中点,M 为 PC 的中点, ∴MO 为△PAC 的中位线. ∴PA∥MO. ∵PA 平面 MBD,MO  平面 MBD, ∴PA∥平面 MBD. （六）拓展提升 如图 11，已知平行四边形 ABCD 和平行四边形 ACEF 所在的平面相交于 AC,M 是线段 EF 的中点. 图 11 求证:AM∥平面 BDE. 证明：设 AC∩BD=O，连接 OE， ∵O、M 分别是 AC、EF 的中点，ACEF 是平行四边形， ∴四边形 AOEM 是平行四边形. ∴AM∥OE. ∵OE  平面 BDE，AM  平面 BDE，∴AM∥平面 BDE. （七）课堂小结 知识总结：利用线面平行的判定定理证明线面平行. 方法总结：利用平面几何中的平行线截比例线段定理，三角形的中位线性质等知识促成 “线线平行”向“线面平行”的转化. （八）作业 课本习题 2.2 A 组 3、4.