- 2021-06-16 发布 |
- 37.5 KB |
- 4页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
人教A数学必修一奇偶性导学案
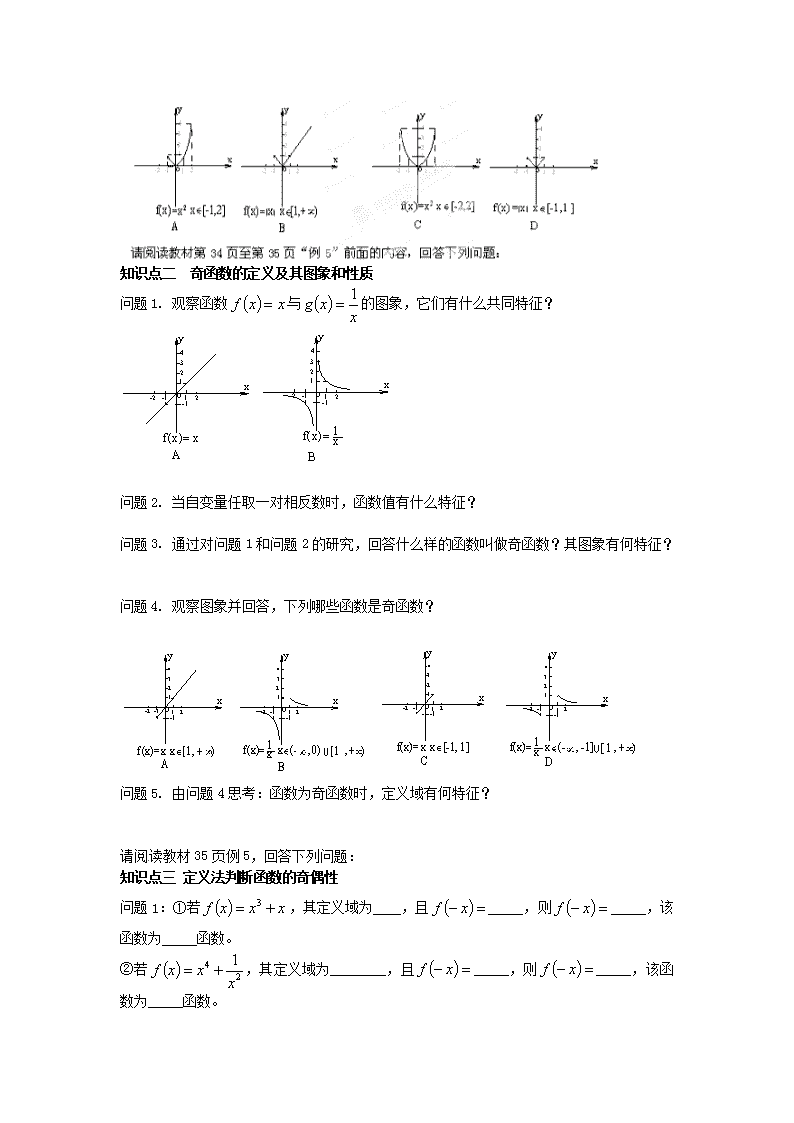
高中数学人教版必修1:1.3.2奇偶性 姓名: 班级: 组别: 组名: 【学习目标】 1. 了解奇、偶函数的定义,能运用函数图象理解和研究函数的性质. 2. 会利用定义判断具体函数的奇偶性. 3. 通过学习培养学生观察、抽象的能力,以及从特殊到一般的概括、归纳问题的能力. 【重点难点】 重点:函数奇偶性定义及其几何意义. 难点:判断函数奇偶性的方法与格式. 【知识链接】 轴对称和中心对称图形. 【学习过程】 请阅读教材第33页至第34页“观察”之前的内容,尝试回答以下问题: 知识点一 偶函数的定义及其图象和性质 问题1. 观察函数和的图象,它们有什么共同特征? 问题2. 计算: , ; , 。 , ; , 。 通过计算,你有什么发现? 问题3. 通过对问题1和问题2的研究,回答什么样的函数叫做偶函数?其图象有何特征? 问题4. 观察图象并回答,下列哪些函数是偶函数? 知识点二 奇函数的定义及其图象和性质 问题1. 观察函数与的图象,它们有什么共同特征? 问题2. 当自变量任取一对相反数时,函数值有什么特征? 问题3. 通过对问题1和问题2的研究,回答什么样的函数叫做奇函数?其图象有何特征? 问题4. 观察图象并回答,下列哪些函数是奇函数? 问题5. 由问题4思考:函数为奇函数时,定义域有何特征? 请阅读教材35页例5,回答下列问题: 知识点三 定义法判断函数的奇偶性 问题1:①若,其定义域为____,且_____,则_____,该函数为_____函数。 ②若,其定义域为________,且_____,则_____,该函数为_____函数。 问题2.尝试总结定义法判断函数奇偶性的一般步骤。 【基础达标】 A1.尝试用定义法判断下列函数的奇偶性 ①; ②; ③; ④ ; ⑤ B2.设函数为奇函数,若,则_____. C3.已知偶函数在上为增函数,则和的大小关系是( ) A. B. C.= D.无法确定 D4.判断函数的奇偶性. D5.已知奇函数,在定义域上是减函数,解不等式 【课堂小结】 1. 知识小结: 奇函数和偶函数的定义: 奇函数和偶函数的图象特征: 2. 方法小结: 定义法判断函数奇偶性的步骤: 【当堂检测】 C1.已知函数在上是偶函数,在上是单调函数,且 则下列不等式一定成立的是( ) A. B. C. D. 【课后反思】 本节课我最大的收获是 我还存在的疑惑是 我对导学案的建议是 查看更多