2019届二轮复习三角变换与解三角形课件（27张）（全国通用）

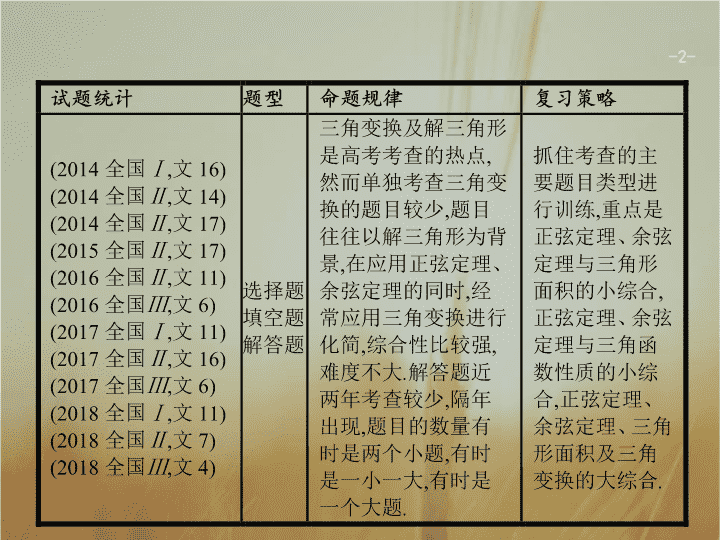
2019届二轮复习三角变换与解三角形课件（27张）（全国通用）

3.2 　三角变换与解三角形 - 2 - - 3 - 命题热点一 命题热点二 命题热点三 命题热点四 三角恒等变换及求值 【思考】 三角变换的基本思路及技巧有哪些? 例 1 D - 4 - 命题热点一 命题热点二 命题热点三 命题热点四 题后反思 从函数名、角、运算三方面进行差异分析 , 变换的基本思路是 : 异角化同角 , 异名化同名 , 高次化低次 ; 常用的技巧是 : 切化弦、降幂公式、用三角公式转化出现特殊角 . - 5 - 命题热点一 命题热点二 命题热点三 命题热点四 - 6 - 命题热点一 命题热点二 命题热点三 命题热点四 正、余弦定理的简单应用 【思考】 应用正、余弦定理需要的条件及解决的问题有哪些? 例 2 (1)设 △ ABC 的内角 A , B , C 所对边的长分别为 a , b , c ,若 b cos C+c cos B=a sin A ,则 △ ABC 的形状为( 　　 ) A.锐角三角形 B.直角三角形 C.钝角三角形 D.不确定 答案 解析 解析 关闭 答案 解析 关闭 - 7 - 命题热点一 命题热点二 命题热点三 命题热点四 题后反思 1 . 已知两角和一边 , 如已知 A , B 和 c ,由 A+B+C= π 求 C , 由正弦定理求 a , b. 2 . 已知两边和这两边的夹角 , 如已知 a , b 和 C , 应先用余弦定理求 c , 再应用正弦定理先求较短边所对的角 , 最 后利用 A+B+C= π , 求另一角 . 3 . 已知两边和其中一边的对角 , 如已知 a , b 和 A , 应先用正弦定理求 B , 由 A+B+C= π 求 C , 再由正弦定理或余弦定理求 c , 要注意解可能有多种情况 . 4 . 已知三边 a , b , c , 可应用余弦定理求 A , B , C ( 或先用余弦定理求出最大边所对的角 , 再用正弦定理及三角形内角和定理求另外两个内角 ) . - 8 - 命题热点一 命题热点二 命题热点三 命题热点四 对点训练 2 在 △ ABC 中 , 内角 A , B , C 所对的边分别为 a , b , c , 已知 a sin A= 4 b sin B , ac= ( a 2 -b 2 -c 2 ) . (1) 求 cos A 的值 ; (2) 求 sin(2 B-A ) 的值 . - 9 - 命题热点一 命题热点二 命题热点三 命题热点四 - 10 - 命题热点一 命题热点二 命题热点三 命题热点四 解三角形 【思考】 在解三角形中 , 一般要用到哪些知识 ? 例 3 在 △ ABC 中 , D 是 BC 上的点 , AD 平分 ∠ BAC , △ ABD 面积是 △ ADC 面积的 2 倍 . - 11 - 命题热点一 命题热点二 命题热点三 命题热点四 (2) 因为 S △ ABD ∶ S △ ADC =BD ∶ DC , 所以 BD= . 在 △ ABD 和 △ ADC 中 , 由余弦定理知 AB 2 =AD 2 +BD 2 - 2 AD·BD cos ∠ ADB , AC 2 =AD 2 +DC 2 - 2 AD·DC cos ∠ ADC. 故 AB 2 + 2 AC 2 = 3 AD 2 +BD 2 + 2 DC 2 = 6 . 由 (1) 知 AB= 2 AC , 所以 AC= 1 . - 12 - 命题热点一 命题热点二 命题热点三 命题热点四 题后反思 关于解三角形问题 , 一般要用到三角形内角和定理、正弦定理、余弦定理及有关三角形的性质 , 常见的三角变换方法和原则都适用 . 同时 , 要注意 “ 三统一 ”, 即 “ 统一角、统一函数、统一结构 ”, 这是使问题获得解决的突破口 . - 13 - 命题热点一 命题热点二 命题热点三 命题热点四 对点训练 3 如图 , 在 ▱ ABCD 中 , AB= 4, AD= 2, ∠ DAB= 60 ° , ∠ BCD= 120 ° . (1) 当 BC=CD 时 , 求 △ BCD 的面积 ; (2) 设 ∠ CBD=θ , 记四边形 ABCD 的周长为 f ( θ ), 求 f ( θ ) 的表达式 , 并求出它的最大值 . - 14 - 命题热点一 命题热点二 命题热点三 命题热点四 - 15 - 命题热点一 命题热点二 命题热点三 命题热点四 - 16 - 命题热点一 命题热点二 命题热点三 命题热点四 解三角形与三角变换的综合问题 【思考】 在三角形中,对于含有边角关系的等式如何进行运算? 例 4 已知 a , b , c 分别为 △ ABC 三个内角 A , B , C 的对边, c= a sin C-c cos A. (1)求 A ; (2)若 a= 2, △ ABC 的面积为 ,求 b , c. - 17 - 命题热点一 命题热点二 命题热点三 命题热点四 - 18 - 命题热点一 命题热点二 命题热点三 命题热点四 题后反思 对于一个解三角形的综合问题 , 若条件是既有边又有角的关系式 , 在进行运算时有两种方法 : 一是先应用正弦定理把边转化为角 , 再利用三角恒等变换进行化简整理 ; 二是先应用余弦定理把角转化为边 , 再进行字母的代数运算 , 使关系式得到简化 . - 19 - 命题热点一 命题热点二 命题热点三 命题热点四 对点训练 4 在 △ ABC 中 , 角 A , B , C 的对边分别为 a , b , c. 已知 b= 3, =- 6, S △ ABC = 3, 求 A 和 a. - 20 - 命题热点一 命题热点二 命题热点三 命题热点四 - 21 - 规律总结 拓展演练 1 . 三角恒等变形的基本思路: (1)“化异名为同名”“化异次为同次”“化异角为同角”; (2)“切化弦”“1”的代换; (3)角的变换是三角变换的核心,如 β = ( α + β ) - α ,2 α = ( α + β ) + ( α - β )等 . 2 . 倍角、半角公式应用的技巧:公式的正用、逆用和变形用 . 3 . 在处理三角形中的边角关系时,一般全部化为角的关系,或全部化为边的关系 . 题中若出现边的一次式一般采用到正弦定理,出现边的二次式一般采用到余弦定理 . 正弦定理的形式多样,其中 a= 2 R sin A , b= 2 R sin B , c= 2 R sin C 能够实现边角互化 . 4 . 在解三角形中,三角形内角和定理起着重要作用,在解题中要注意根据这个定理确定角的范围,确定三角函数值的符号,防止出现增解等扩大范围的现象 . - 22 - 规律总结 拓展演练 C - 23 - 规律总结 拓展演练 A - 24 - 规律总结 拓展演练 C 解析 由 , 得 c 2 =a 2 +b 2 - 2 ab sin C. 又由余弦定理 c 2 =a 2 +b 2 - 2 ab cos C , ∴ sin C= cos C , - 25 - 规律总结 拓展演练 4 . △ ABC 的内角 A , B , C 的对边分别为 a , b , c. 已知 C= 60 ° , b= , c= 3,则 A= 　　　　　 .   75 ° 因为 b

查看更多