- 2021-06-16 发布 |
- 37.5 KB |
- 4页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高中数学(人教版必修2)配套练习 第二章2.2.3 直线与平面平行的性质
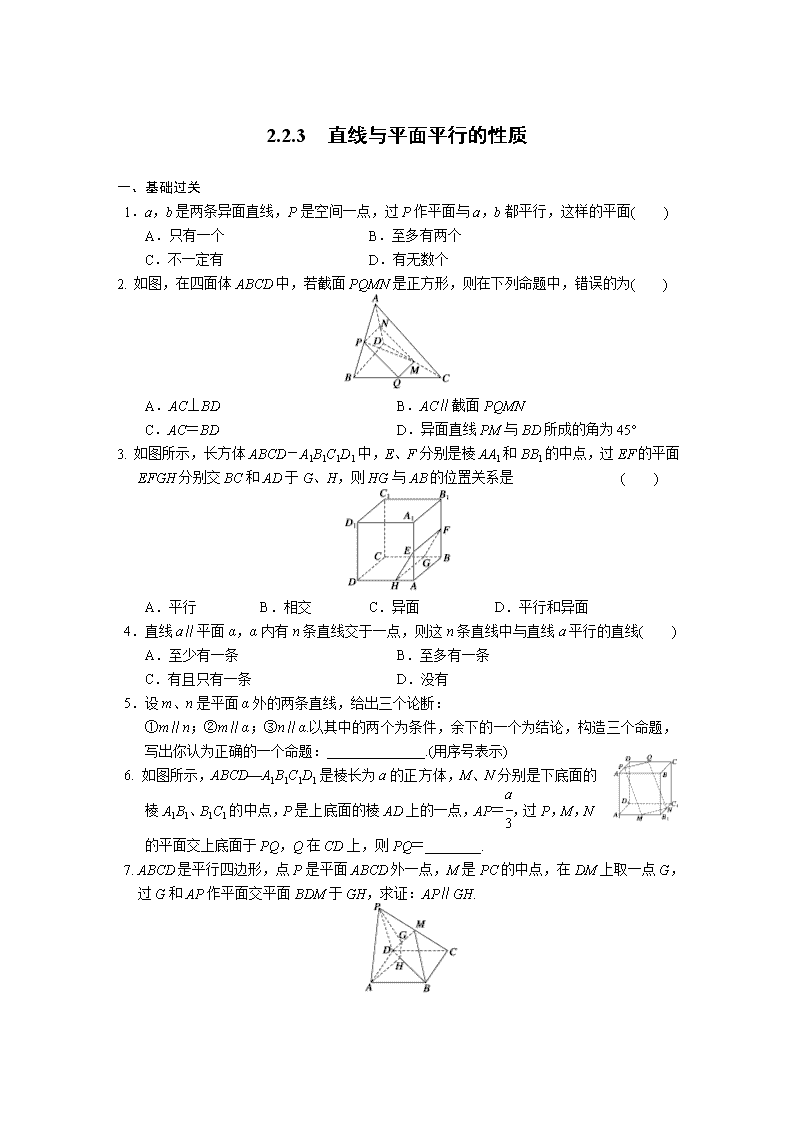
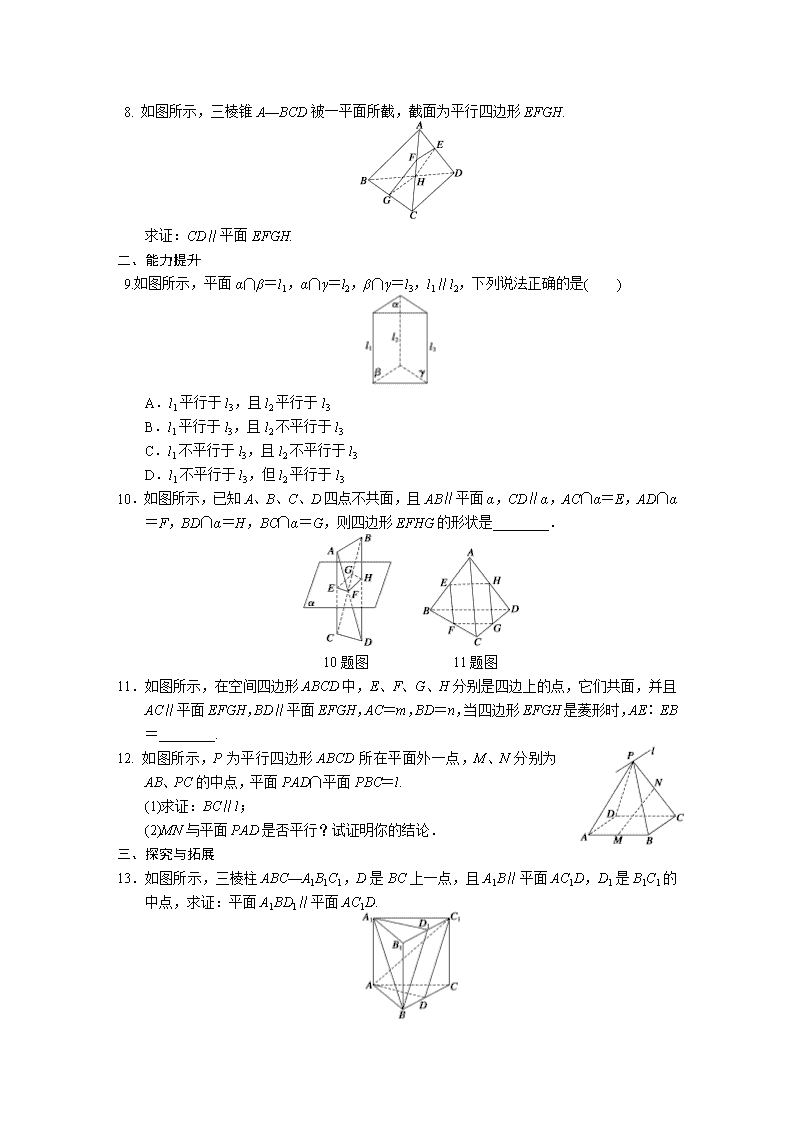
2.2.3 直线与平面平行的性质 一、基础过关 1.a,b 是两条异面直线,P 是空间一点,过 P 作平面与 a,b 都平行,这样的平面( ) A.只有一个 B.至多有两个 C.不一定有 D.有无数个 2. 如图,在四面体 ABCD 中,若截面 PQMN 是正方形,则在下列命题中,错误的为( ) A.AC⊥BD B.AC∥截面 PQMN C.AC=BD D.异面直线 PM 与 BD 所成的角为 45° 3. 如图所示,长方体 ABCD-A1B1C1D1 中,E、F 分别是棱 AA1 和 BB1 的中点,过 EF 的平面 EFGH 分别交 BC 和 AD 于 G、H,则 HG 与 AB 的位置关系是 ( ) A.平行 B.相交 C.异面 D.平行和异面 4.直线 a∥平面α,α内有 n 条直线交于一点,则这 n 条直线中与直线 a 平行的直线( ) A.至少有一条 B.至多有一条 C.有且只有一条 D.没有 5.设 m、n 是平面α外的两条直线,给出三个论断: ①m∥n;②m∥α;③n∥α.以其中的两个为条件,余下的一个为结论,构造三个命题, 写出你认为正确的一个命题:______________.(用序号表示) 6. 如图所示,ABCD—A1B1C1D1 是棱长为 a 的正方体,M、N 分别是下底面的 棱 A1B1、B1C1 的中点,P 是上底面的棱 AD 上的一点,AP=a 3 ,过 P,M, N 的平面交上底面于 PQ,Q 在 CD 上,则 PQ=________. 7. ABCD 是平行四边形,点 P 是平面 ABCD 外一点,M 是 PC 的中点,在 DM 上取一点 G, 过 G 和 AP 作平面交平面 BDM 于 GH,求证:AP∥GH. 8. 如图所示,三棱锥 A—BCD 被一平面所截,截面为平行四边形 EFGH. 求证:CD∥平面 EFGH. 二、能力提升 9.如图所示,平面α∩β=l1,α∩γ=l2,β∩γ=l3,l1∥l2,下列说法正确的是( ) A.l1 平行于 l3,且 l2 平行于 l3 B.l1 平行于 l3,且 l2 不平行于 l3 C.l1 不平行于 l3,且 l2 不平行于 l3 D.l1 不平行于 l3,但 l2 平行于 l3 10.如图所示,已知 A、B、C、D 四点不共面,且 AB∥平面α,CD∥α,AC∩α=E,AD∩α =F,BD∩α=H,BC∩α=G,则四边形 EFHG 的形状是________. 10 题图 11 题图 11.如图所示,在空间四边形 ABCD 中,E、F、G、H 分别是四边上的点,它们共面,并且 AC∥平面 EFGH,BD∥平面 EFGH,AC=m,BD=n,当四边形 EFGH 是菱形时,AE∶EB =________. 12. 如图所示,P 为平行四边形 ABCD 所在平面外一点,M、N 分别为 AB、 PC 的中点,平面 PAD∩平面 PBC=l. (1)求证:BC∥l; (2)MN 与平面 PAD 是否平行?试证明你的结论. 三、探究与拓展 13.如图所示,三棱柱 ABC—A1B1C1,D 是 BC 上一点,且 A1B∥平面 AC1D,D1 是 B1C1 的 中点,求证:平面 A1BD1∥平面 AC1D. 答案 1.C 2.C 3.A 4.B 5.①②⇒③(或①③⇒②) 6.2 2 3 a 7.证明 如图所示,连接 AC 交 BD 于 O,连接 MO, ∵ABCD 是平行四边形, ABCD 是平行四边形,点 P 是平面 ABCD 外一点,M 是 PC 的中点,在 DM 上取一点 G, 过 G 和 AP 作平面交平面 BDM 于 GH,求证:AP∥GH. ∴O 是 AC 中点,又 M 是 PC 的中点, ∴AP∥OM. 根据直线和平面平行的判定定理, 则有 PA∥平面 BMD. ∵平面 PAHG∩平面 BMD=GH, 根据直线和平面平行的性质定理, 则有 AP∥GH. 8.证明 ∵四边形 EFGH 为平行四边形, ∴EF∥GH. 又 GH⊂平面 BCD,EF⊄平面 BCD. ∴EF∥平面 BCD. 而平面 ACD∩平面 BCD=CD,EF⊂平面 ACD,∴EF∥CD. 而 EF⊂平面 EFGH,CD⊄平面 EFGH, ∴CD∥平面 EFGH. 9.A 10.平行四边形 11.m∶n 12.(1)证明 因为 BC∥AD,AD⊂平面 PAD, BC⊄平面 PAD,所以 BC∥平面 PAD. 又平面 PAD∩平面 PBC=l,BC⊂平面 PBC,所以 BC∥l. (2)解 MN∥平面 PAD. 证明如下: 如图所示,取 PD 中点 E. 连接 EN、AE. 又∵N 为 PC 中点,∴EN 綊 1 2AB ∴EN 綊 AM,∴四边形 ENMA 为平行四边形,∴AE∥MN. 又∵AE⊂平面 PAD,MN⊄平面 PAD, ∴MN∥平面 PAD. 13.证明 连接 A1C 交 AC1 于点 E, ∵四边形 A1ACC1 是平行四边形, ∴E 是 A1C 的中点,连接 ED, ∵A1B∥平面 AC1D, 平面 A1BC∩平面 AC1D=ED, ∴A1B∥ED, ∵E 是 A1C 的中点,∴D 是 BC 的中点.又∵D1 是 B1C1 的中点,∴BD1∥C1D, 又∵C1D⊂平面 AC1D,BD1⊄平面 AC1D, ∴BD1∥平面 AC1D, 又 A1B∩BD1=B, ∴平面 A1BD1∥平面 AC1D.查看更多