2020届二轮复习正弦定理和余弦定理课件（27张）（全国通用）

2020届二轮复习正弦定理和余弦定理课件（27张）（全国通用）

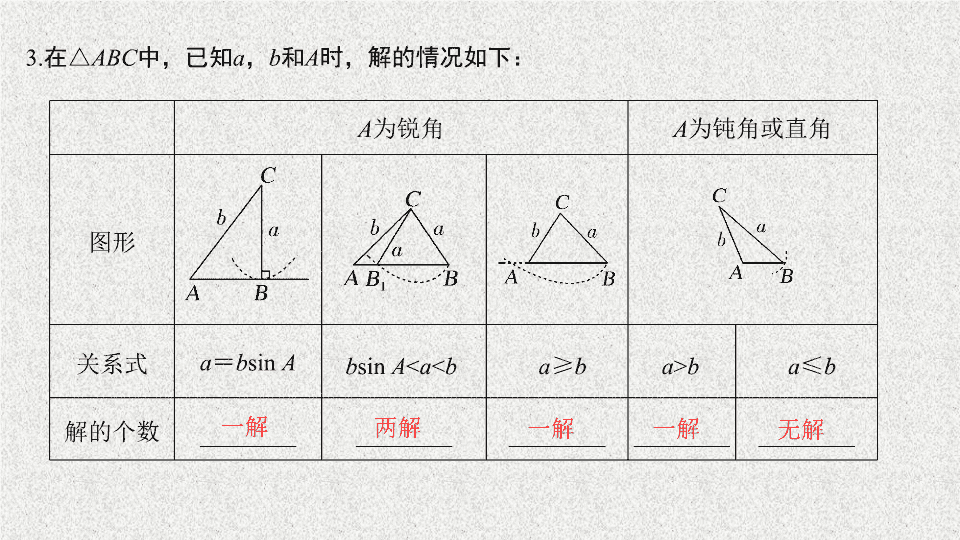
知 识 梳 理 1 . 正、余弦定理 在 △ ABC 中，若角 A ， B ， C 所对的边分别是 a ， b ， c ， R 为 △ ABC 外接圆半径，则 b 2 ＋ c 2 － 2 bc cos A c 2 ＋ a 2 － 2 ca cos B a 2 ＋ b 2 － 2 ab cos C 2 R sin B 2 R sin C sin A ∶ sin B ∶ sin C 3. 在 △ ABC 中，已知 a ， b 和 A 时，解的情况如下：   A 为锐角 A 为钝角或直角 图形 关系式 a ＝ b sin A b sin A < a < b a ≥ b a > b a ≤ b 解的个数 ________ ________ ________ ________ ________ 一解 两解 一解 一解 无解 [ 微点提醒 ] 1. 三角形中的三角函数关系 (1)sin( A ＋ B ) ＝ sin C ； (2)cos( A ＋ B ) ＝－ cos C ； 2. 三角形中的射影定理 在 △ ABC 中， a ＝ b cos C ＋ c cos B ； b ＝ a cos C ＋ c cos A ； c ＝ b cos A ＋ a cos B . 3. 在 △ ABC 中，两边之和大于第三边，两边之差小于第三边， A > B ⇔ a > b ⇔ sin A > sin B ⇔ cos A sin B ，则 A > B .( 　　 ) (3) 在 △ ABC 的六个元素中，已知任意三个元素可求其他元素 .( 　　 ) (4) 当 b 2 ＋ c 2 － a 2 >0 时， △ ABC 为锐角三角形；当 b 2 ＋ c 2 － a 2 ＝ 0 时， △ ABC 为直角三角形；当 b 2 ＋ c 2 － a 2 <0 时， △ ABC 为钝角三角形 .( 　　 ) 解析　 (1) 三角形中三边之比等于相应的三个内角的正弦值之比 . (3) 已知三角时，不可求三边 . (4) 当 b 2 ＋ c 2 － a 2 >0 时，三角形 ABC 不一定为锐角三角形 . 答案 　 (1) × 　 (2) √ 　 (3) × 　 (4) × 2. ( 必修 5P56A5 改编 ) 在 △ ABC 中， AB ＝ 5 ， AC ＝ 3 ， BC ＝ 7 ，则 ∠ BAC ＝ ( 　　 ) 答案　 C 3. ( 必修 5P65B2 改编 ) 在 △ ABC 中， a cos A ＝ b cos B ，则这个三角形的形状为 ________. 解析　 由正弦定理，得 sin A cos A ＝ sin B cos B ， 即 sin 2 A ＝ sin 2 B ，所以 2 A ＝ 2 B 或 2 A ＝ π － 2 B ， 所以这个三角形为等腰三角形或直角三角形 . 答案　 等腰三角形或直角三角形 答案 　 D 答案　 A ∴ 由 a 2 ＝ b 2 ＋ c 2 － 2 bc cos A ，可得 8 ＝ 4 c 2 ＋ c 2 － 3 c 2 ， 解得 c ＝ 2( 舍负 ) ，则 b ＝ 4. 考点一　利用正、余弦定理解三角形 结合 b < c 得 B ＝ 45° ，则 A ＝ 180° － B － C ＝ 75°. (2) ∵ ( a ＋ b )(sin A － sin B ) ＝ ( c － b )sin C ， ∴ 由正弦定理得 ( a ＋ b )( a － b ) ＝ c ( c － b ) ，即 b 2 ＋ c 2 － a 2 ＝ bc . 答案　 (1)75° 　 (2)B 　 (3)C 规律方法 　 1. 三角形解的个数的判断：已知两角和一边，该三角形是确定的，其解是唯一的；已知两边和一边的对角，该三角形具有不唯一性，通常根据三角函数值的有界性和大边对大角定理进行判断 . 2. 已知三角形的两边和其中一边的对角解三角形 . 可用正弦定理，也可用余弦定理 . 用正弦定理时，需判断其解的个数，用余弦定理时，可根据一元二次方程根的情况判断解的个数 . 解析　 (1) 由题意得 sin( A ＋ C ) ＋ sin A (sin C － cos C ) ＝ 0 ， ∴ sin A cos C ＋ cos A sin C ＋ sin A sin C － sin A cos C ＝ 0 ， 则有 cos 2 C ＋ cos C ＝ 0 ，即 2cos 2 C ＋ cos C － 1 ＝ 0 ， 由 4sin B ＝ 3sin A ，得 4 b ＝ 3 a ， ① 又 a － b ＝ 1 ， ② 联立 ① ， ② 得 a ＝ 4 ， b ＝ 3 ， ∴ 满足条件的三角形有 2 个 . 答案　 (1)B 　 (2)A 　 (3)B 考点二　判断三角形的形状 A. 钝角三角形 B. 直角三角形 C. 锐角三角形 D. 等边三角形 (2) 设 △ ABC 的内角 A ， B ， C 所对的边分别为 a ， b ， c ，若 b cos C ＋ c cos B ＝ a sin A ，则 △ ABC 的形状为 ( 　　 ) A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 不确定 又 B ∈ (0 ， π) ，所以 sin B >0 ， 所以 sin C 0 ，所以 cos B <0 ， 即 B 为钝角，所以 △ ABC 为钝角三角形 . (2) 由正弦定理得 sin B cos C ＋ sin C cos B ＝ sin 2 A ， ∴ sin( B ＋ C ) ＝ sin 2 A ，即 sin A ＝ sin 2 A . 答案 　 (1)A 　 (2)B 规律方法 　 1. 判定三角形形状的途径： (1) 化边为角，通过三角变换找出角之间的关系； (2) 化角为边，通过代数变形找出边之间的关系，正 ( 余 ) 弦定理是转化的桥梁 . 2. 无论使用哪种方法，都不要随意约掉公因式，要移项提取公因式，否则会有漏掉一种形状的可能 . 注意挖掘隐含条件，重视角的范围对三角函数值的限制 . 【训练 2 】 若将本例 (2) 中条件变为 “ c － a cos B ＝ (2 a － b )cos A ” ，判断 △ ABC 的形状 . 解　 ∵ c － a cos B ＝ (2 a － b )cos A ， C ＝ π － ( A ＋ B ) ， ∴ 由正弦定理得 sin C － sin A cos B ＝ 2sin A cos A － sin B cos A ， ∴ sin A cos B ＋ cos A sin B － sin A cos B ＝ 2sin A cos A － sin B cos A ， ∴ cos A (sin B － sin A ) ＝ 0 ， ∴ cos A ＝ 0 或 sin B ＝ sin A ， ∴△ ABC 为等腰或直角三角形 . 考点三　和三角形面积、周长有关的问题 多维探究 角度 1 　与三角形面积有关的问题 (1) 求 c ； (2) 设 D 为 BC 边上一点，且 AD ⊥ AC ，求 △ ABD 的面积 . 即 c 2 ＋ 2 c － 24 ＝ 0 ，解得 c ＝－ 6( 舍去 ) ， c ＝ 4. 角度 2 　与三角形周长有关的问题 则 ( b ＋ c ) 2 ≤ 64 ，即 b ＋ c ≤ 8( 当且仅当 b ＝ c ＝ 4 时等号成立 ) ， ∴△ ABC 周长＝ a ＋ b ＋ c ＝ 4 ＋ b ＋ c ≤ 12 ，即最大值为 12. 答案　 12 【训练 3 】 (2019· 潍坊一模 ) △ ABC 的内角 A ， B ， C 的对边分别为 a ， b ， c ，已知 ( a ＋ 2 c )cos B ＋ b cos A ＝ 0. (1) 求 B ； (2) 由余弦定理，得 9 ＝ a 2 ＋ c 2 － 2 ac cos B . ∴ a 2 ＋ c 2 ＋ ac ＝ 9 ，则 ( a ＋ c ) 2 － ac ＝ 9. 解　 (1) 由已知及正弦定理得 (sin A ＋ 2sin C )cos B ＋ sin B cos A ＝ 0 ， (sin A cos B ＋ sin B cos A ) ＋ 2sin C cos B ＝ 0 ， sin( A ＋ B ) ＋ 2sin C cos B ＝ 0 ， 又 sin( A ＋ B ) ＝ sin C ，且 C ∈ (0 ， π) ， sin C ≠ 0 ， [ 思维升华 ] 1 . 正弦定理和余弦定理其主要作用是将已知条件中的边、角关系转化为角的关系或边的关系 . 2. 在已知关系式中，既含有边又含有角，通常的解题思路是：先将角都化成边或边都化成角，再结合正弦定理、余弦定理即可求解 .