【北师大版】2021版高考数学一轮复习第二章函数及其应用2.9 函数的应用
- 1 -
2.9 函数的应用
核心考点·精准研析
考点一 利用图像刻画实际问题
1.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了 2014 年 1 月至 2016 年 12 月期间
月接待游客量(单位:万人)的数据,绘制了下面的折线图
根据该折线图,下列结论错误的是 ( )
A.月接待游客量逐月增加
B.年接待游客量逐年增加
C.各年的月接待游客量高峰期大致在 7,8 月份
D.各年 1 月至 6 月的月接待游客量相对 7 月至 12 月,波动性更小,变化比较平稳
【解析】选 A.由题图可知,2014 年 8 月到 9 月的月接待游客量在减少,则 A 选项错误,故选 A.
2.如图所示,一直角墙角,两边的长度足够长,在 P 处有一棵树与两墙的距离分别是 a(m)(0
8 时,由于函数在[a,12]上为减函数,
所以当 x=a 时,矩形面积取最大值 Smax=f(a)=a(16-a).
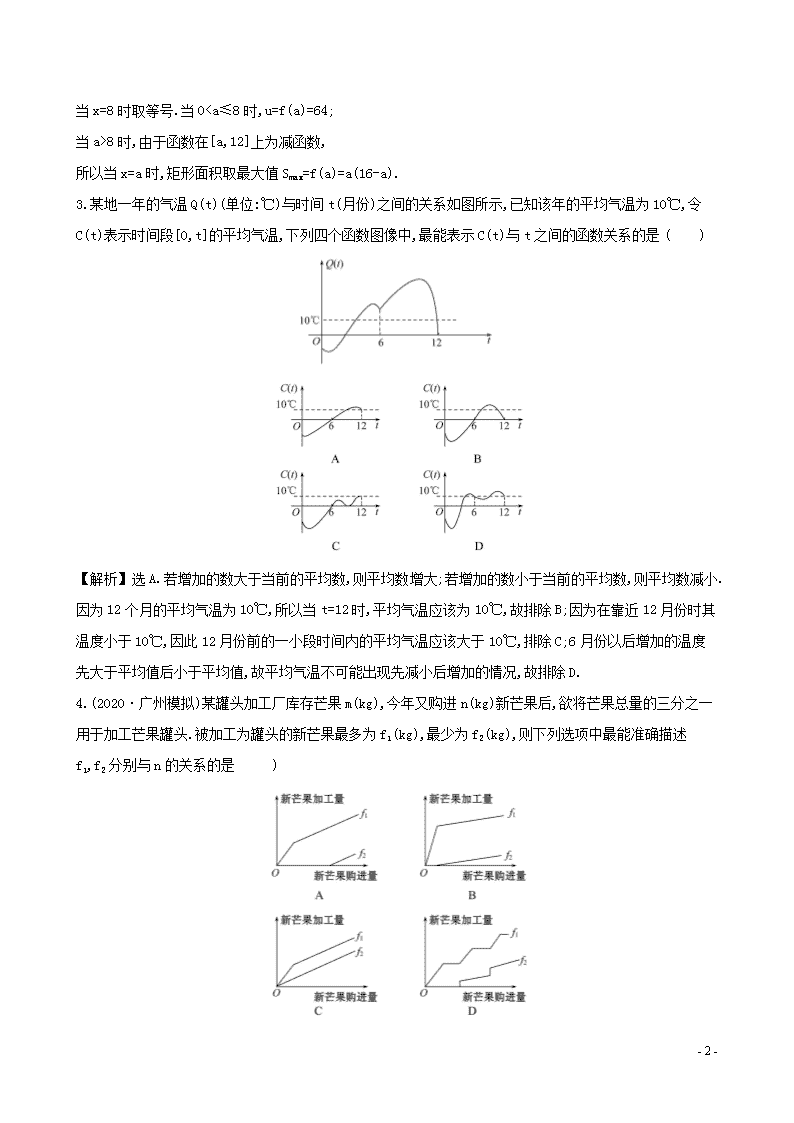
3.某地一年的气温 Q(t)(单位:℃)与时间 t(月份)之间的关系如图所示,已知该年的平均气温为 10℃,令
C(t)表示时间段[0,t]的平均气温,下列四个函数图像中,最能表示 C(t)与 t 之间的函数关系的是 ( )
【解析】选 A.若增加的数大于当前的平均数,则平均数增大;若增加的数小于当前的平均数,则平均数减小.
因为 12 个月的平均气温为 10℃,所以当 t=12 时,平均气温应该为 10℃,故排除 B;因为在靠近 12 月份时其
温度小于 10℃,因此 12 月份前的一小段时间内的平均气温应该大于 10℃,排除 C;6 月份以后增加的温度先
大于平均值后小于平均值,故平均气温不可能出现先减小后增加的情况,故排除 D.
4.(2020·广州模拟)某罐头加工厂库存芒果 m(kg),今年又购进 n(kg)新芒果后,欲将芒果总量的三分之一
用于加工芒果罐头.被加工为罐头的新芒果最多为 f1(kg),最少为 f2(kg),则下列选项中最能准确描述 f1,f2
分别与 n 的关系的是 )
- 3 -
【解析】选 A.要使得被加工为罐头的新芒果最少,尽量使用库存芒果,即当 ≤m,n≤2m 时,f2=0,当 n>2m
时,f2= -m= >0,对照图像舍去 C,D;
要使得被加工为罐头的新芒果最多,则尽量使用新芒果,即当 ≤n,n≥ 时 f1= ,当 >n,n<
时 f1=n,因为 <2m,所以选 A.
判断函数图像与实际问题变化过程相吻合的两种方法
(1)构建函数模型法:当根据题意易构建函数模型时,先建立函数模型,再结合模型选图像.
(2)验证法:根据实际问题中两变量的变化快慢等特点,结合图像的变化趋势,验证是否吻合,从中排除不符
合实际的情况,选择出符合实际情况的答案.
考点二 已知函数模型求解实际问题
【典例】1.某产品的总成本 y(万元)与产量 x(台)之间的函数关系是 y=
3 000+20x-0.1x2(00)的函数模型称为“对勾”函数模型,“对勾”函数模型的单调区间及最
值如下
(1)该函数在(-∞,- ]和[ ,+∞)上单调递增,在[- ,0)和(0, ]上单调递减.
(2)当 x>0 时,x= 时取最小值 2 ,
当 x<0 时,x=- 时取最大值-2 .
初等函数模型及其应用
【典例】(2019·马鞍山模拟)某高校为提升科研能力,计划逐年加大科研经费投入.若该高校 2018 年全年
投入科研经费 1 300 万元,在此基础上,每年投入的科研经费比上一年增长 12%,则该高校全年投入的科研经
费开始超过 2 000 万元的年份是(参考数据:lg 1.12≈0.05,lg 1.3≈0.11,lg 2≈0.30) ( )
A.2020 年 B.2021 年
C.2022 年 D.2023 年
【解析】选 C.若 2019 年是第 1 年,则第 n 年全年投入的科研经费为 1 300×1.12n 万元,由 1 300×1.12n>2 000,
可得 lg 1.3+nlg 1.12>lg 2,所以 n×0.05>0.19,得 n>3.8,即 n≥4,所以第 4 年,即 2022 年全年投入的科
研经费开始超过 2 000 万元.
每年投入的科研经费比上一年增长 12%,说明每年经费是上一年的多少倍?
提示:说明每年经费是上一年的 1.12 倍.
对勾函数模型及其应用
【典例】(2020·榆林模拟)某养殖场需定期购买饲料,已知该场每天需要饲料 200 千克,每千克饲料的价格
为 1.8 元,饲料的保管费与其他费用平均每千克每天 0.03 元,购买饲料每次支付运费 300 元.求该场多少天
购买一次饲料才能使平均每天支付的总费用最少.
【解析】设该场 x(x∈N*)天购买一次饲料,平均每天支付的总费用为 y 元.
因为饲料的保管费与其他费用每天比前一天少 200×0.03=6(元),所以 x 天饲料的保管费与其他费用共是
6(x-1)+6(x-2)+…+6=(3x2-3x)(元).
- 7 -
从而有 y= (3x2-3x+300)+200×1.8= +3x+357≥417,当且仅当 =3x,即 x=10 时,y 有最小值.故该场
10 天购买一次饲料才能使平均每天支付的总费用最少.
对勾函数求最值应注意什么?
提示:对勾函数求最值一定要注意该函数的单调性,然后再求最值.
分段函数模型及其应用
【典例】(2020·银川模拟)大气温度 y(℃)随着距离地面的高度 x(km)的增加而降低,当在高度不低于 11 km
的高空时气温几乎不变.设地面气温为 22℃,大约每上升 1 km 大气温度降低 6℃,则 y 关于 x 的函数关系式
为 .
【解析】由题意知,y 是关于 x 的分段函数,x=11 为分界点,易得其解析式为 y=
答案:y=
实际问题中分段函数的适用条件是什么?
提示:实际问题中有些变量间的关系不能用同一个关系式给出,而是由几个不同的关系式构成,如出租车计
价与路程之间的关系,应构建分段函数模型求解.
1.要制作一个容积为 16 m3,高为 1 m 的无盖长方体容器,已知该容器的底面造价是每平方米 20 元,侧面造
价是每平方米 10 元,则该容器的最低总造价是 元.
- 8 -
【解析】设长方体容器底面矩形的长、宽分别为 x m,y m,则 y= ,所以容器的总造价为
z=2(x+y)×1×10+20xy=20 +20×16,由基本不等式得,z=20 +20×16≥
40 +320=480,当且仅当 x=y=4,即底面是边长为 4 m 的正方形时,总造价最低.
答案:480
2.(2019·北京高考)李明自主创业,在网上经营一家水果店,销售的水果中有草莓、京白梨、西瓜、桃,价
格依次为 60 元/盒、65 元/盒、80 元/盒、90 元/盒.为增加销量,李明对这四种水果进行促销:一次购买水
果的总价达到 120 元,顾客就少付 x 元.每笔订单顾客网上支付成功后,李明会得到支付款的 80%.
①当 x=10 时,顾客一次购买草莓和西瓜各 1 盒,需要支付 元;
②在促销活动中,为保证李明每笔订单得到的金额均不低于促销前总价的七折,则 x 的最大值
为 .
【解析】①价格为 60+80=140 元,达到 120 元,少付 10 元,所以需支付 130 元.
②设促销前总价为 a 元,a≥120,李明得到金额 l(x)=(a-x)×80%≥0.7a,0≤x≤120,即 x≤ 恒成立,又 最
小值为 =15,所以 x 最大值为 15.
答案:①130 ②15
1.(2019·深圳模拟)某校甲、乙两食堂某年 1 月份的营业额相等,甲食堂的营业额逐月增加,并且每月的增
加值相同;乙食堂的营业额也逐月增加,且每月增加的百分率相同.已知本年 9 月份两食堂的营业额又相等,
则本年 5 月份 ( )
A.甲食堂的营业额较高
B.乙食堂的营业额较高
C.甲、乙两食堂的营业额相同
D.不能确定甲、乙哪个食堂的营业额较高
【解析】选 A.设甲、乙两食堂 1 月份的营业额均为 m,甲食堂的营业额每月增加 a(a>0),乙食堂的营业额每
月增加的百分率为 x,由题意可得,m+8a=m×(1+x)8,则 5 月份甲食堂的营业额 y1=m+4a,乙食堂的营业额
- 9 -
y2=m×(1+x)4= ,因为 - =(m+4a)2-m(m+8a)=16a2>0,所以 y1>y2,故本年 5 月份甲食堂
的营业额较高.
2.一个工厂生产某种产品每年需要固定投资 100 万元,此外每生产 1 件该产品还需要增加投资 1 万元,年产
量为 x(x∈N*)件.当 x≤20 时,年销售总收入为(33x-x2)万元;当 x>20 时,年销售总收入为 260 万元.记该工
厂生产并销售这种产品所得的年利润为 y 万元,则 y 与 x 的函数关系式为 ,该工厂的年产量为
件时,所得年利润最大(年利润=年销售总收入-年总投资).
【解析】年销售总收入减去年总投资即可得到年利润,年总投资为(x+100)万元,故函数关系式为
y= 当 020 时,y<140.故年产量为 16 件时,年利润最大.
答案:y= 16