- 2021-06-16 发布 |
- 37.5 KB |
- 9页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高考数学一轮复习练案44第七章立体几何第三讲空间点直线平面之间的位置关系含解析
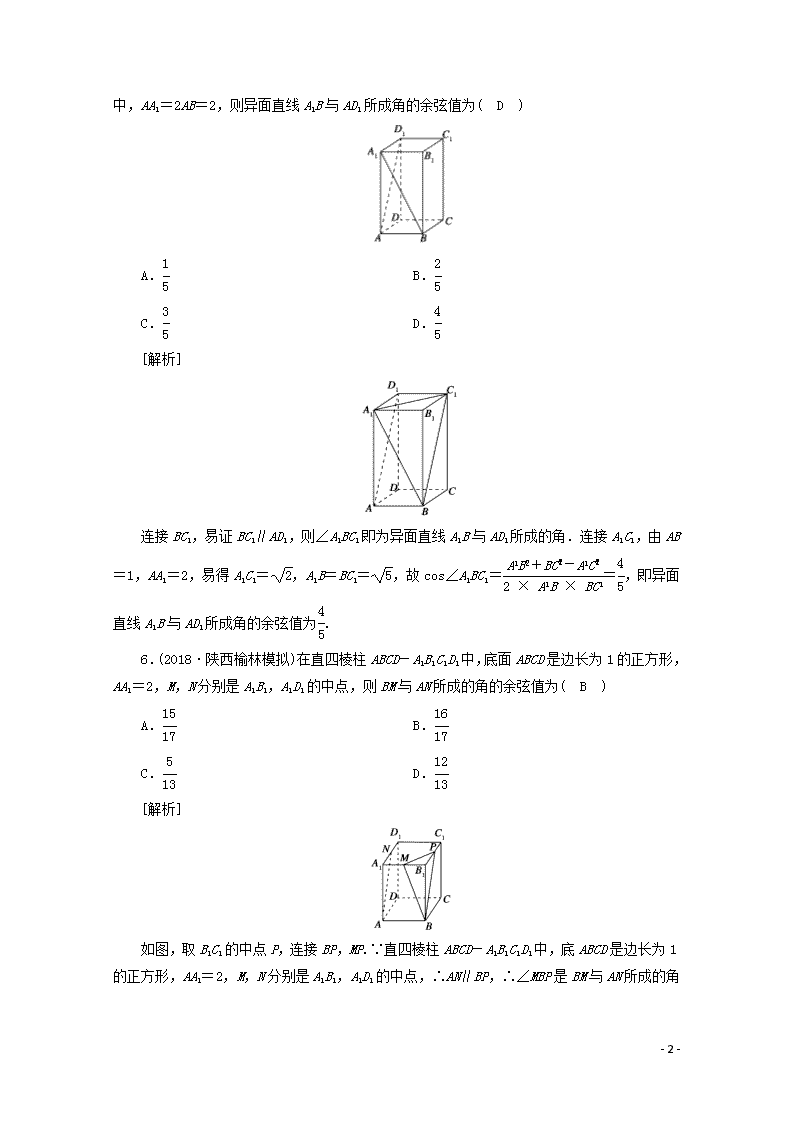
[练案44]第三讲 空间点、直线、平面之间的位置关系 A组基础巩固 一、单选题 1.在空间中,下列命题正确的是( D ) A.经过三个点有且只有一个平面 B.经过一个点和一条直线有且只有一个平面 C.经过一个点且与一条直线平行的平面有且只有一个 D.经过一个点且与一条直线垂直的平面有且只有一个 2.四条线段顺次首尾相连,它们最多可确定的平面个数为( A ) A.4 B.3 C.2 D.1 [解析] 首尾相连的四条线段每相邻两条确定一个平面,所以最多可以确定四个平面. 3.a,b,c是两两不同的三条直线,下面四个命题中,真命题是( C ) A.若直线a,b异面,b,c异面,则a,c异面 B.若直线a,b相交,b,c相交,则a,c相交 C.若a∥b,则a,b与c所成的角相等 D.若a⊥b,b⊥c,则a∥c [解析] 若直线a,b异面,b,c异面,则a,c相交、平行或异面;若a,b相交,b,c相交,则a,c相交、平行或异面;若a⊥b,b⊥c,则a,c相交、平行或异面;由异面直线所成的角的定义知C正确.故选C. 4.如图所示,平面α∩平面β=l,A∈α,B∈α,AB∩l=D,C∈β,C∉l,则平面ABC与平面β的交线是( C ) A.直线AC B.直线AB C.直线CD D.直线BC [解析] 由题意知,D∈l,l⊂β,所以D∈β, 又因为D∈AB,所以D∈平面ABC, 所以点D在平面ABC与平面β的交线上. 又因为C∈平面ABC,C∈β, 所以点C在平面β与平面ABC的交线上, 所以平面ABC∩平面β=CD. 5.(2020·青岛模拟)如图,在底面为正方形,侧棱垂直于底面的四棱柱ABCD-A1B1C1D1 - 9 - 中,AA1=2AB=2,则异面直线A1B与AD1所成角的余弦值为( D ) A. B. C. D. [解析] 连接BC1,易证BC1∥AD1,则∠A1BC1即为异面直线A1B与AD1所成的角.连接A1C1,由AB=1,AA1=2,易得A1C1=,A1B=BC1=,故cos∠A1BC1==,即异面直线A1B与AD1所成角的余弦值为. 6.(2018·陕西榆林模拟)在直四棱柱ABCD-A1B1C1D1中,底面ABCD是边长为1的正方形,AA1=2,M,N分别是A1B1,A1D1的中点,则BM与AN所成的角的余弦值为( B ) A. B. C. D. [解析] 如图,取B1C1的中点P,连接BP,MP.∵直四棱柱ABCD-A1B1C1D1中,底ABCD是边长为1的正方形,AA1=2,M,N分别是A1B1,A1D1的中点,∴AN∥BP,∴∠MBP是BM与AN所成的角(或所成角的补角).BM=BP==,MP==,∴cos∠MBP= - 9 - ==.∴BM与AN所成的角的余弦值为.故选B. 7.(2019·江西高安期末)三棱柱ABC-A1B1C1中,侧棱AA1垂直于底面A1B1C1,底面三角形A1B1C1是正三角形,E是BC的中点,则下列叙述正确的是( A ) ①CC1与B1E是异面直线; ②AE与B1C1是异面直线,且AE⊥B1C1; ③AC⊥平面ABB1A1; ④A1C1∥平面AB1E. A.② B.①③ C.①④ D.②④ [解析] 对于①,CC1,B1E都在平面BB1CC1内,故错误;可排除B、C,对于④,A1C1所在的平面与平面AB1E相交,且A1C1与交线有公共点,故错误,选A项. 8.(2019·福建长汀、连城一中等六校联考)已知正三棱锥S-ABC的底面边长为2、侧棱长为2,D、E分别是AB、SC的中点,则异面直线DE与BC所成的角的大小为( B ) A.90° B.60° C.45° D.30° [解析] 作SO⊥平面ABC于O,则C、O、D共线,由题意可知CO=,∴cos∠SCD=,取SB的中点H,连HE,HD,则HE∥BC,从而∠HED即为异面直线DE与BC所成的角,且HE=1,DH=,又DE2=DC2+CE2-2DC·CE·cos∠DCS=4,∴∠EHD=90°,又EH=DE,∴∠HED=60°,故选B. - 9 - 9.(2019·福建漳州二模)在正方体ABCD-A1B1C1D1中,O为AC的中点,则异面直线AD1与OC1所成角的余弦值为( C ) A. B. C. D. [解析] 由题意知O∈BD,连BC1,则BC1∥AD1, ∴∠OC1B即为AD1与OC1所成的角, 设正方体棱长为a, 则BO=a,BC1=a, 又BC1=DC1,∴C1O⊥BD,∴sin∠OC1B=, 从而cos∠OC1B=,故选C. 10.(2019·内蒙古包头模拟)如图,在正方体ABCD-A1B1C1D1中,点P在线段AD1上运动,则异面直线CP与BA1所成的角θ的取值范围是( D ) A.(0,) B.(0,] C.[0,] D.(0,] 二、多选题 11.如图是正方体或四面体,P,Q,R,S分别是所在棱的中点,这四个点共面的是( ABC ) - 9 - [解析] 在A图中分别连接PS,QR,易证PS∥QR,∴P,Q,R,S共面;在C图中分别连接PQ,RS,易证PQ//RS,∴P,Q,R,S共面;如图所示,在B图中过P,Q,R,S可作一正六边形,故四点共面;D图中PS与 QR为异面直线,∴四点不共面,故选ABC. 12.(原创)三个平面可将空间分成( )部分( ACD ) A.4 B.5 C.7 D.8 [解析] 三个平面可将空间分成4或6或7或8部分. 13.(2020·湖北名师联盟模拟改编)如图,正方体ABCD-A1B1C1D1中,点E,,F分别是AB,A1D1的中点,O为正方形A1B1C1D1的中心,则下列结论错误的是( ABD ) A.直线EF,AO是异面直线 B.直线EF,BB1是相交直线 C.直线EF与BC1所成角为30° D.直线EF与BB1所成角的余弦值为 [解析] OF綊AE,EF、AO是相交直线,A错; EF、BB1是异面直线,B错; 如图,OF綊BE, - 9 - ∴EF∥BO, ∴∠C1BO为EF与BC1所成的角, 设正方体棱长为2, 则BC1=2,OC1=,BO=, ∴BC=OC+BO,即BO⊥OC1, ∴∠OBC1=30°,C对; EF与BB1所成角的余弦值为,D错;故选ABD. 三、填空题 14.(2020·郑州质检)在正方体ABCD-A1B1C1D1中,M、N分别为A1B1,BB1的中点,则异面直线AM与CN所成角的余弦值为 . [解析] 如图所示,取AB的中点E,连接B1E,则AM∥B1E,取EB的中点F,连接FN,则B1E∥FN,因此AM∥FN,则直线FN与CN所夹的锐角或直角为异面直线AM与CN所成的角,设AB=1,连接CF,在△CFN中,CN=,FN=,CF=.由余弦定理,得cos∠CNF==. 15.(2019·云南模拟)在正三棱柱ABC-A1B1C1中,若AB=BB1,则异面直线AB1与C1B所成的角是__90°__. [解析] 将正三棱柱补成四棱柱,如图,设BB1=,则AB=2,连接AD1,BD1,则BC1∥AD1,∴∠D1AB1即为异面直线AB1与BC1所成的角,又由题意易知AB1=AD1=,B1D1=2,∴B1D=AB+AD,∴∠B1AD1=90°. - 9 - 另解1:本题若取A1B1的中点D,连DC1,易证AB1⊥平面BDC1,从而AB1⊥BC1. 另解2:可建立空间直角坐标系,用向量法求解. B组能力提升 1.(2020·甘肃诊断)直三棱柱ABC-A′B′C′中,∠ABC=90°,AB=4,BC=2,BB′=,则异面直线AC′与B′C所成角的余弦值为 . [解析] 连接BC′,交CB′于E,则E为BC′为中点,取AB中点F,连接EF,故EF∥AC′,则∠FEC或其补角为所求,又EF=AC′=,FC==2,CE=B′C=,在三角形EFB中,cos∠FEC=,故答案为. 2. (2020·河北衡水中学调研)如图,圆柱的轴截面ABCD为正方形,E为弧的中点,则异面直线AE与BC所成角的余弦值为( D ) A. B. C. D. [解析] 由题意可知AD∥BC,∴∠EAD即为异面直线AE与BC所成的角,设圆柱上、下底面圆心为O,O1,连OE、OA、ED,不妨设正方形ABCD的边长为2,则AO=,从而AE=ED=,则cos∠EAD==,即AE与BC所成角的余弦值为,故选D. - 9 - 3.(多选题)如图是侧棱长和底面边长都相等的正四棱锥的平面展开图,M,N,P,Q分别是边BF,AB,CD,DH的中点,则在这个正四棱锥,下列四个结论正确的为( BD ) A.MN和CD平行 B.CE和PQ平行 C.MN和PE所成的角为60° D.EP和AB垂直 [解析] 正棱锥直观图如图,显然MN与CD异面,A错;B对;连AP,由MN∥AE知,∠AEP为异面直线MN与PE所成的角,设四棱锥的棱长为2a,则AP=a,PE=a,∴cos∠AEP==,C错;∵PE⊥CD,CD∥AB,∴PE⊥AB,D对.故选B、D. 4.(2019·西安模拟)如图,四边形ABCD和四边形ADPQ均为正方形,它们所在的平面互相垂直,则异面直线AP与BD所成的角为__60°__. [解析] 将图形补成正方体,如图,连BH,HD,则∠HBD即为异面直线AP与BD所成的角,又BH=BD=HD,∴∠HBD=60°. 5. - 9 - 如图所示,三棱锥P-ABC中,PA⊥平面ABC,∠BAC=60°,PA=AB=AC=2,E是PC的中点. (1)求证:AE与PB是异面直线; (2)求异面直线AE和PB所成角的余弦值; (3)求三棱锥A-EBC的体积. [解析] (1)证明:假设AE与PB共面,设平面为α, ∵A∈α,B∈α,E∈α,∴平面α即为平面ABE, ∴P∈平面ABE,这与P∉平面ABE矛盾, ∴AE与PB是异面直线. (2)取BC的中点F,连接EF、AF,则EF∥PB,所以∠AEF或其补角就是异面直线AE和PB所成角. ∵∠BAC=60°,PA=AB=AC=2,PA⊥平面ABC, ∴AF=,AE=,EF=, cos∠AEF==, ∴异面直线AE和PB所成角的余弦值为. (3)因为E是PC的中点,所以E到平面ABC的距离为PA=1, VA-EBC=VE-ABC=×(×2×)×1=. - 9 -查看更多