- 2021-06-16 发布 |
- 37.5 KB |
- 18页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
浙江省杭州市第二中学2020届高三上学期第一次月考数学试题
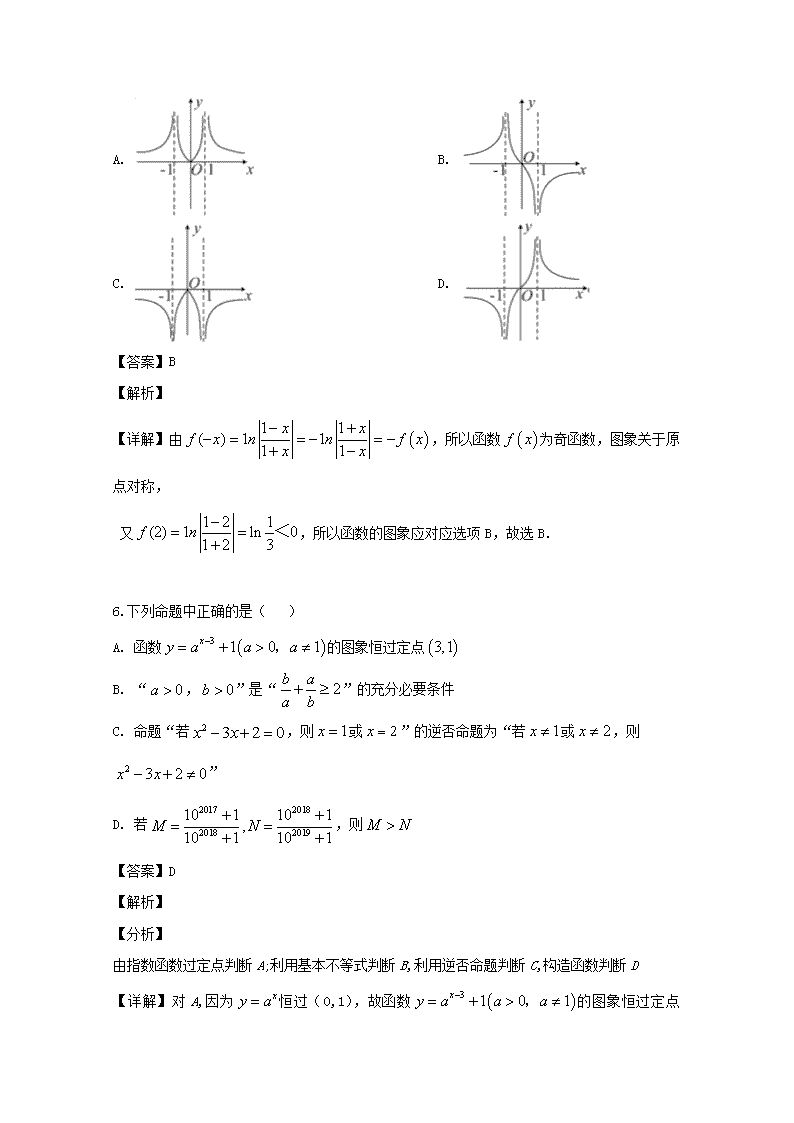
杭州二中高三第一学期第一次月考数学试题 一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的. 1.已知集合,,则=( ) A. B. C. D. 【答案】B 【解析】 ∵集合 ∴集合或 ∵集合 ∴集合 ∴ 故选B. 2.若,则的大小关系是 ( ) A. B. C. D. 【答案】C 【解析】 【分析】 直接利用对数函数和指数函数的单调性求解. 【详解】∵0<a=,b=log0.51.2<log0.51=0,c=1.20.5>1.20=1, ∴b<a<c. 故选:C. 【点睛】本题考查对数值大小的比较,考查了对数函数和指数函数的单调性,是基础题. 3.已知复数对应复平面上的点,复数满足,则( ) A. B. C. D. 【答案】A 【解析】 【分析】 由已知利用复数代数形式的乘除运算化简求得z2,再求模长即可. 【详解】由已知可得z1=﹣1+i, ∴, ∴|z2|. 故选:A. 【点睛】本题考查复数代数形式的乘除运算,考查复数模的求法,是基础题. 4.函数,的值域是( ) A. B. C. D. 【答案】A 【解析】 【分析】 利用二倍角的余弦函数化简函数为一个角的一个三角函数的形式,然后求解函数的值域. 【详解】因为函数y=cos2x+sin2x=cos2xcos2xcos2x.因为x∈R,所以cos2x∈[﹣1,1], 所以cos2x∈[0,1]. 故选:A. 【点睛】本题考查三角函数的恒等变换,二倍角的余弦函数的应用,求三角函数的值域是解题的关键,考查计算能力. 5.函数的大致图象为( ) A. B. C. D. 【答案】B 【解析】 【详解】由,所以函数为奇函数,图象关于原点对称, 又,所以函数的图象应对应选项B,故选B. 6.下列命题中正确的是( ) A. 函数的图象恒过定点 B. “,”是“”的充分必要条件 C. 命题“若,则或”的逆否命题为“若或,则” D. 若,则 【答案】D 【解析】 【分析】 由指数函数过定点判断A;利用基本不等式判断B,利用逆否命题判断C,构造函数判断D 【详解】对A,因为恒过(0,1),故函数的图象恒过定点 ,故A错误; 对B, 的充分必要条件是,故B错误; 对C, 命题“若,则或”的逆否命题为“若且,则”,故C错误; 对D,令,则,易得函数为单调递减函数,故,则D正确 故选:D 【点睛】本题考查命题真假,熟练掌握函数单调性,基本不等式,逆否命题等知识是关键,是中档题 7.已知内角的对边分别为,若,,则的形状是( ) A. 等腰三角形 B. 等边三角形 C. 等腰直角三角形 D. 等腰三角形或直角三角形 【答案】D 【解析】 【分析】 利用余弦定理将化边代入,结合求解即可 【详解】由题 当,三角形直角三角形 当,则,又,则三角形为等腰三角形 故选:D 【点睛】本题考查余弦定理,注意角化边的应用,是基础题,注意等式两边不能随便约分,是易错题 8.函数(),满足,且对任意,都有,则以下结论正确的是 A. B. C. D. 【答案】A 【解析】 【详解】解:函数f(x)满足, ∴f(x)关于点(,0)对称, 且对任意x∈R,都有, ∴x是f(x)的对称轴, 令x=0,得﹣f(0)=asin0+bcos0=b=f()=0, ∴b=0,f(x)=asinωx,A正确; ∴f(x)是定义域R上的奇函数,B错误; 可得a≠0,b=0,ab,C错误; 由题意,ω=6k+3,k∈Z,∴D错误; 综上,正确的结论是A. 故选:A. 9.若不等式组(为常数),表示的平面区域的面积8,则的最小值为( ) A. B. C. D. 2 【答案】B 【解析】 【分析】 画出满足条件的(a为常数)表示的平面区域,根据目标函数z=x2+y的几何意义是曲线y=﹣x2+z与y轴交点的纵坐标,利用数形结合可以得到答案. 【详解】满足约束条件的可行域如下图所示, 若可行域的面积为8,则a=2 设z=x2+y 由图可得当z=x2+y与直线相切时z最小,联立两曲线得x2-x-z=0,,得 ,此时x,y,故x2+y取最小值, 故选:B. 【点睛】本题考查的知识点是简单线性规划,其中画出约束条件对应的可行域是解答本题的关键. 10.已知函数在区间上满足,且.设,,则当时,下列不等式成立的是( ) A. B. C. D. 不能确定 【答案】A 【解析】 【分析】 求导数,利用f(x)+f′(x)<0,可得F(x)=exf(x)的单调性,根据0<x<1,x,由已知F(x)>F(),即可得出结论. 【详解】令F(x)=exf(x),∴F′(x)=ex[f(x)+f′(x)]; 又∵f(x)+f′(x)<0,∴F′(x)<0, ∴F(x)是(0,+∞)上的减函数; 令0<x<1,则x,由已知F(x)>F(),可得f(x)f(), 下面证明:,即证明x+2lnx>0, 令g(x)x+2lnx,则: g′(x)0,g(x)在(0,1)↓,g(x)>g(1), 即, ∴xf(x)f(),即 故选:A 【点睛】本题考查导数知识的综合运用,考查函数的单调性,考查大小比较,正确构造函数求导是关键. 二、填空题。 11.在中,,,,,则的最小值为______ , 又若,则________. 【答案】 (1). (2). 【解析】 【分析】 利用平面向量数量积的运算律和定义计算,将其转化为有关于的二次函数的最小值,可得出的最小值,由,得出,利用平面向量数量积的运算律和定义可求出实数的值. 【详解】 , 所以当时, 取最小值; 因为,所以,解得,故答案为:;. 【点睛】本题考查平面向量模的最值的计算以及垂直向量数量积的转化,解题时应充分转化为平面向量数量积,考查运算求解能力,属于中等题. 12.已知函数,则函数的增区间是____,最小值是_____ 【答案】 (1). (2). 4 【解析】 【分析】 去绝对值分段,得的解析式,则增区间和最小值可求 【详解】易知,则函数的增区间是, 又,则函数的最小值为4 故答案为 ; 4 【点睛】本题考查分段函数的性质,考查函数增减性及最值,是基础题 13.若锐角满足,则______;函数的单调增区间为______. 【答案】 (1). (2). 【解析】 【分析】 根据题意由同角三角函数和二倍角求出φ的值,利用降幂公式化简函数f(x), 再求出它的单调增区间. 【详解】锐角φ满足sinφ﹣cosφ, ∴1﹣2sinφcosφ, ∴sin2φ; 又sinφ, ∴2φ, 解得φ; ∴函数f(x)=sin2(x+φ) cos(2x), ∴2kπ≤2x2kπ+π,k∈Z; 解得kπx≤kπ,k∈Z; ∴f(x)的单调增区间为[kπ,kπ](k∈Z). 故答案为 ; 【点睛】本题考查了三角函数的图象与性质的应用问题,准确利用三角变换化简是关键,是中档题. 14.已知函数,若,则____;有_________个零点 【答案】 (1). 1或或 (2). 4 【解析】 【分析】 分情况讨论正负解方程即可求解,则其乘积可求,利用换元法结合内外层函数求解根的个数即可 【详解】当均大于0,则或或或,此时1或或 当均小于0,不合题意舍去. 又令,则,故 或 解得 则与交点个数分别1个,0个,3个,综上有4个零点 故答案为1或或 ; 4 【点睛】本题考查分段函数及性质,函数的零点,注意函数复合的应用,是难题 15.已知函数,则不等式的解集是______. 【答案】 【解析】 【分析】 先判断函数的奇偶性和单调性,再构造函数解不等式即可 【详解】,故为奇函数,且单调递减,则令,故 为奇函数且单调递减,故 等价于,即 ,即,解得 故答案为 【点睛】本题考查函数的奇偶性和单调性,准确判断的奇偶性和单调性,构造新函数是关键,是中档题 16.已知都为正实数,且,则的最小值为______. 【答案】9 【解析】 【分析】 将通分整理代入所求式子,配凑基本不等式形式求解即可 【详解】则 且,则=,当且仅当等号成立 故答案为9 【点睛】本题考查基本不等式求最值,将条件灵活变形是关键,是中档题 17.已知是平面上两个定点,平面上的动点满足,若对于任意的,不等式恒成立,则实数的最小值为______. 【答案】 【解析】 【分析】 建立坐标系,得点的轨迹方程,分离参量求范围即可求解 【详解】不妨设,以A为原点,AB所在直线为x轴建立直角坐标系,则 , 设 故动点的轨迹为圆,由恒成立,则 故答案为 【点睛】本题考查圆的轨迹方程,平面问题坐标化的思想,是难题 三、解答题:解答应写出文字说明、证明过程或演算步骤。 18.已知函数 (1)求的值; (2)当时,求函数的值域. 【答案】(1)1;(2) 【解析】 【分析】 (1)利用二倍角公式结合辅助角公式化简解析式,即可求值;(2)由正弦函数的性质求值域即可 详解】(1) (2)由(1)知,, 当时 由,得的值域为. 【点睛】本题考查三角变换,熟记公式准确化简是关键,是基础题 19.已知两个非零向量,且, (1)求的夹角; (2)若,求的最小值. 【答案】(1);(2) 【解析】 【分析】 (1)由垂直结合数量积运算得,再利用模长公式结合得,即可求解夹角;(2)利用模长公式计算结合基本不等式求最值即可 【详解】(1)由可得 ,即 又 则 所以 故 (2)若 则的最小值为,当时,即时,取得最小值。 【点睛】本题考查向量的数量积,模长夹角运算,其中模长最值是易错点,是中档题 20.已知锐角中,角的对边分别为,向量, ,且. (1)求角; (2)求的取值范围. 【答案】(1);(2) 【解析】 【分析】 (1)由结合二倍角公式求解即可;(2)利用正弦定理边化角,再利用内角和为,结合三角变换化为的函数求解即可 详解】(1)∵,∴,∴ ,由锐角故 (2). 为锐角三角形,则 ∴,所以. 故的取值范围是. 【点睛】本题考查数量积垂直的坐标运算,三角恒等变换,及正弦定理,准确计算是关键,是中档题 21.已知函数,() (1)当时,若存在实数,当时,恒成立,求实数的最大值。 (2)若对任意,总存在唯一,使得成立.求实数的取值范围. 【答案】(1)4;(2)或 【解析】 【分析】 (1)不等式恒成立,转化为()恒成立,换元转化为二次函数求最值即可求解;(2)对讨论求值域,由的值域为值域的子集,利用集合的包含关系列不等式求解即可 【详解】(1),∵存在实数,当时,恒成立; 即恒成立.()恒成立. 设,则 ∴, 即,且 ,∴实数最大值是4。 (2),∵∴ ∴函数的值域为 其次,由题意知:,且对任意,总存在唯一,使得.以下分三种情况讨论: ①当时,则,解得; ②当时,则,解得; ③当时,则或,解得; 综上:a的取值范围是a≤﹣2或a. 【点睛】本题考查二次函数不等式恒成立问题,双变元问题,注意题目的等价转化是关键,是中档题 22.已知函数, . (1)若与的图象在公共点处有相同的切线,求切线方程; (2)若为整数,且恒成立,求的最小值. 【答案】(1);(2)2 【解析】 【分析】 (1)设公共点为,利用切线斜率相等,及点在两个函数上列方程组求解即可求解切线方程;(2)分离参数,构造函数求最值即可求解 【详解】(1)设公共点为,则有,解得,故切线方程是 (2) ∵恒成立,∴恒成立 恒成立,令,, 令,,单调递增, ,所以存在使, 所以在上单调递增,在单调递减, ,因为为整数,所以的最小值为2. 【点睛】本题考查导数的几何意义,利用导数解决不等式恒成立问题,函数最值问题,准确转化是关键,是中档题 查看更多