- 2021-06-16 发布 |
- 37.5 KB |
- 22页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
宁夏回族自治区银川一中2020届高三第三次模拟考试数学(文)试题
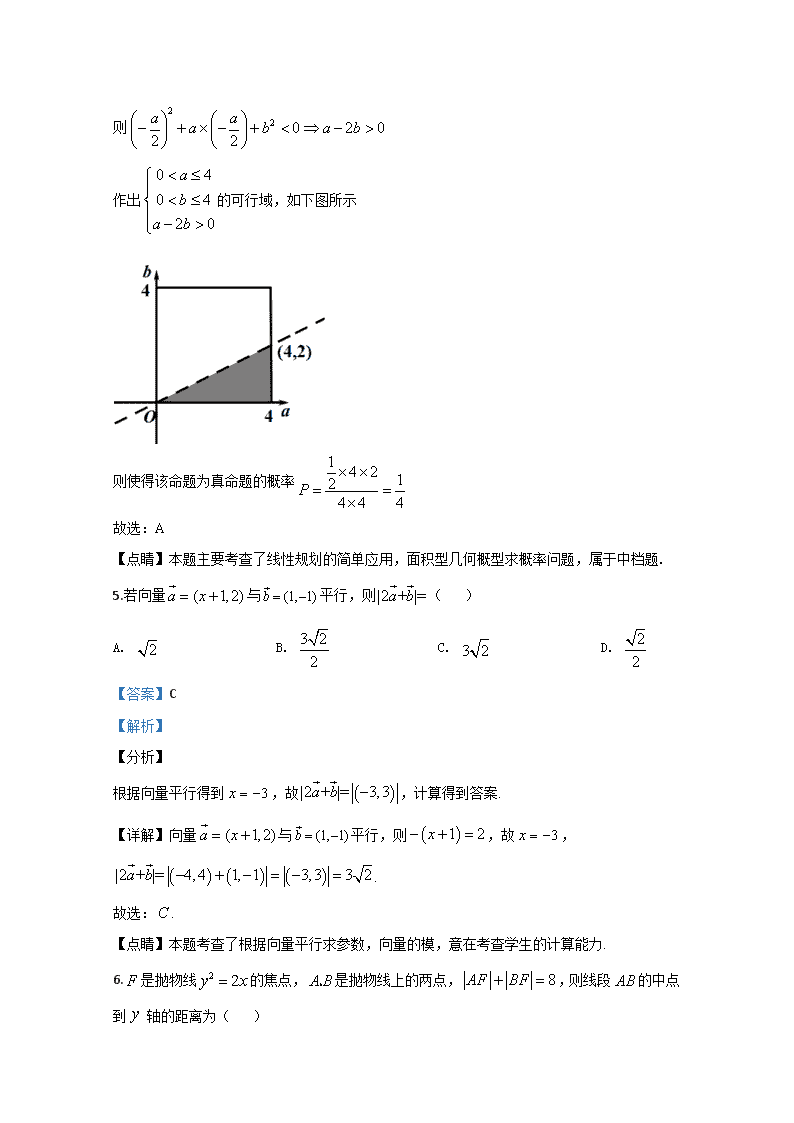
2020年普通高等学校招生全国统一考试 文科数学试题卷 注意事项: 1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上. 2.作答时,务必将答案写在答题卡上.写在本试卷及草稿纸上无效. 3.考试结束后,将本试卷和答题卡一并交回. 一、选择题:本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.已知集合,则=( ) A. B. C. D. 【答案】D 【解析】 【分析】 先求出集合A,B,再求集合B的补集,然后求 【详解】,所以 . 故选:D 【点睛】此题考查的是集合的并集、补集运算,属于基础题. 2.若复数z与其共轭复数满足,则( ) A B. C. 2 D. 【答案】A 【解析】 【分析】 设,则,得到答案. 【详解】设,则,故,, ,. 故选:. 【点睛】本题考查了复数的计算,意在考查学生的计算能力. 3.已知双曲线的离心率为,则其渐近线为( ) A. 2x+y=0 B. C. D. 【答案】D 【解析】 本题由双曲线标准方程,离心率出发来求解其渐近线,主要考察学生对双曲线概念,基本关系的理解与应用,属于简单题型. 请在此填写本题解析! 解 因为, =25, 因为+,所以,+=25 即化简得=,所以答案为D. 4.在区间内随机取两个数,则使得“命题‘,不等式成立’为真命题”的概率为( ) A. B. C. D. 【答案】A 【解析】 【分析】 由该命题为真命题得出,画出不等式组表示的平面区域,根据几何概型的计算公式求解即可. 【详解】,不等式成立,即 则 作出的可行域,如下图所示 则使得该命题为真命题的概率 故选:A 【点睛】本题主要考查了线性规划的简单应用,面积型几何概型求概率问题,属于中档题. 5.若向量与平行,则( ) A. B. C. D. 【答案】C 【解析】 【分析】 根据向量平行得到,故,计算得到答案. 【详解】向量与平行,则,故, . 故选:. 【点睛】本题考查了根据向量平行求参数,向量的模,意在考查学生的计算能力. 6.是抛物线的焦点,是抛物线上的两点,,则线段的中点到 轴的距离为( ) A. B. C. D. 【答案】D 【解析】 【分析】 根据抛物线的方程求出准线方程,利用抛物线的定义抛物线上的点到焦点的距离等于到准线的距离,列出方程求出A,B的中点横坐标的和,求出线段AB的中点到y轴的距离 【详解】是抛物线的焦点, ,准线方程, 设, , , 线段AB的中点横坐标为, 线段AB的中点到y轴的距离为 所以D选项是正确的 【点睛】抛物线的弦长问题一般根据第一定义可简化运算. 7.已知是两条不重合的直线,是两个不重合的平面,则下列命题中,错误的是( ) A. 若,则 B. 若,则 C. 若,则 D. 若,则或 【答案】A 【解析】 【分析】 根据直线和平面,平面和平面的位置关系依次判断每个选项得到答案. 【详解】对于:若,则或,故错误;正确. 故选:. 【点睛】本题考查了直线和平面,平面和平面的位置关系,意在考查学生的空间想象能力和推断能力. 8.已知函数的部分图像如图,则的解析式可能是( ) A. B. C. D. 【答案】C 【解析】 【分析】 根据定义域排除A,根据奇偶性排除D,根据单调性排除B,即可得出答案. 【详解】由图象可知,函数在上单调递增,且为奇函数 对A项,由于定义域不是,则A错误; 对B项,当时, ; 则函数在不是单调递增,则B错误; 对C项,,则函数在上单调递增 又,则函数为奇函数,则C正确; 对D项,,则函数不是奇函数,则D错误; 故选:C 【点睛】本题主要考查了根据图象判断解析式,属于中档题. 9.已知函数,,,,则,,的大小关系为( ) A. B. C. D. 【答案】A 【解析】 【分析】 首先判断函数的奇偶性与单调性,再根据指数函数、对数函数的性质得到,,,即可得解; 【详解】解:因为,定义域为, 故函数是奇函数,又在定义域上单调递增,在定义域上单调递减,所以在定义域上单调递增, 由,, 所以 即 故选:A 【点睛】本题考查指数函数、对数函数的性质的应用,属于基础题. 10.天文学中为了衡量星星的明暗程度,古希腊天文学家喜帕恰斯(,又名依巴谷)在公元前二世纪首先提出了星等这个概念.星等的数值越小,星星就越亮;星等的数值越大,它的光就越暗.到了1850年,由于光度计在天体光度测量中的应用,英国天文学家普森()又提出了衡量天体明暗程度的亮度的概念.天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满足.其中星等为的星的亮度为.已知“心宿二”的星等是1.00.“天津四” 的星等是1.25.“心宿二”的亮度是“天津四”的倍,则与最接近的是(当较小时, ) A. 1.24 B. 1.25 C. 1.26 D. 1.27 【答案】C 【解析】 【分析】 根据题意,代值计算,即可得,再结合参考公式,即可估算出结果. 【详解】根据题意可得: 可得,解得, 根据参考公式可得, 故与最接近的是. 故选:C. 【点睛】本题考查对数运算,以及数据的估算,属基础题. 11.已知数列的通项公式是,其中 的部分图像如图所示,为数列的前项和,则的值为( ) A. B. C. D. 【答案】D 【解析】 【分析】 根据图像得到,,,计算每个周期和为0,故,计算得到答案. 【详解】,故,故,, , 故,故,当时满足条件,故, ,,, ,,,,,,每个周期和为0, 故. 故选:. 【点睛】本题考查了数列和三角函数的综合应用,意在考查学生计算能力和综合应用能力. 12.已知函数,若函数有4个零点,则实数的取值范围是( ) A. B. C. D. 【答案】B 【解析】 【分析】 根据函数零点定义可知有四个不同交点,画出函数图像可先求得斜率的大致范围.根据函数在和的解析式,可求得与两段函数相切时的斜率,即可求得的取值范围. 【详解】函数, 函数有4个零点,即有四个不同交点. 画出函数图像如下图所示: 由图可知,当时,设对应二次函数顶点为,则,, 当时,设对应二次函数的顶点为,则,. 所以. 当直线与时的函数图像相切时与函数图像有三个交点,此时,化简可得. ,解得 (舍); 当直线与时的函数图像相切时与函数图像有五个交点,此时,化简可得. ,解得 (舍); 故当有四个不同交点时. 故选:B. 【点睛】本题考查了分段函数解析式的求法,函数零点与函数交点的关系,直线与二次函数相切时的切线斜率求法,属于难题. 二、填空题:本大题共4小题,每小题5分,共20分. 13.我校高一、高二、高三共有学生1800名,为了了解同学们对“智慧课堂”的意见,计划采用分层抽样的方法,从这1800名学生中抽取一个容量为36的样本.若从高一、高二、高三抽取的人数恰好是从小到大排列的连续偶数,则我校高三年级的学生人数为_____. 【答案】700 【解析】 【分析】 设从高三年级抽取的学生人数为2x人,由题意利用分层抽样的定义和方法,求出x的值,可得高三年级的学生人数. 【详解】设从高三年级抽取的学生人数为2x人,则从高二、高一年级抽取的人数分别为2x﹣2,2x﹣4. 由题意可得,∴. 设我校高三年级的学生人数为N,再根据,求得N=700 故答案为:700. 【点睛】本题主要考查分层抽样,属于基础题. 14.已知实数满足,则的最大值为_______. 【答案】22 【解析】 【分析】 ,作出可行域,利用直线的截距与b的关系即可解决. 【详解】作出不等式组表示的平面区域如下图中阴影部分所示, 由可得,观察可知,当直线过点时,取得最大值, 由,解得,即,所以. 故答案为:22. 【点睛】本题考查线性规划中线性目标函数的最值问题,要做好此类题,前提是正确画出可行域,本题是一道基础题. 15.等差数列的前n项和为,,则_____. 【答案】 【解析】 【分析】 计算得到,再利用裂项相消法计算得到答案. 【详解】,,故,故, . 故答案为:. 【点睛】本题考查了等差数列的前n项和,裂项相消法求和,意在考查学生对于数列公式方法的综合应用. 16.在三棱锥中,,点到底面的距离是;则三棱锥的外接球的表面积是_________. 【答案】 【解析】 【分析】 根据线面垂直的判定定理以及勾股定理得出,平面,将三棱锥 放入长方体中,得出长方体的外接球的半径,即为三棱锥的外接球的半径,再由球的表面积公式得出答案. 【详解】取中点为,连接,过点作的垂线,垂足为 平面, 平面 平面, ,平面, 平面,即 在中, ,与重合,即,平面 将三棱锥放入如下图所示的长方体中 则该三棱锥的外接球的半径 所以三棱锥的外接球的表面积 故答案为: 【点睛】本题主要考查了多面体的外接球的问题,涉及了线面垂直的证明,属于中档题. 三、解答题:共70分,解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答. (一)必考题:共60分) 17.某年级教师年龄数据如下表: 年龄(岁) 人数(人) 22 1 28 2 29 3 30 5 31 4 32 3 40 2 合计 20 (1)求这20名教师年龄的众数与极差; (2)以十位数为茎,个位数为叶,作出这20名教师年龄的茎叶图; (3)现在要在年龄为29岁和31岁教师中选2位教师参加学校有关会议,求所选的2位教师年龄不全相同的概率. 【答案】(1)30,18;(2)见解析;(3) 【解析】 试题分析: (1)由所给的年龄数据可得这20名教师年龄的众数为30,极差为18. (2)结合所给的数据绘制茎叶图即可; (3)由题意可知,其中任选2名教师共有21种选法,所选的2位教师年龄不全相同的选法共有12种,结合古典概型计算公式可得所求概率值为. 试题解析: (1)年龄为30岁的教师人数为5,频率最高,故这20名教师年龄的众数为30,极差为最大值与最小值的差,即40-22=18. (2) (3)设事件“所选的2位教师年龄不全相同”为事件A.年龄为29,31岁的教师共有7名,从其中任选2名教师共有=21种选法,3名年龄为29岁的教师中任选2名有3种选法,4名年龄为31岁的教师中任选2名有6种选法,所以所选的2位教师年龄不全相同的选法共有21-9=12种,所以P(A)==. 18.在锐角△ABC中,,________, (1)求角A; (2)求△ABC的周长l的范围. 注:在①,且,②,③这三个条件中任选一个,补充在上面问题中并对其进行求解. 【答案】(1)若选①,(2) 【解析】 【分析】 (1)若选①,,得到,解得答案. (2)根据正弦定理得到,故,根据角度范围得到答案. 【详解】(1)若选①,∵,且 ,,. (2), 故, ,锐角△ABC,故. ,. (1)若选②,,则, ,,,(2)问同上; (1)若选③=+- =×+×-, ,(2)问同上; 【点睛】本题考查了向量的数量积,正弦定理,三角恒等变换,意在考查学生的计算能力和综合应用能力. 19.如图所示多面体中,四边形是正方形,平面平面,,,. (1)求证:; (2)求点D到平面的距离. 【答案】(1)证明见解析;(2) 【解析】 【分析】 (1)利用面面垂直的性质定理,线面垂直的判定定理以及性质,即可证明; (2)利用等体积法求解即可. 【详解】(1)四边形是正方形, 又平面平面,平面平面,平面 平面 又平面 在中, 由余弦定理得,,∴,∴. 又,平面 ∴平面. 又平面 ∴. (2)连结,由(1)可知,平面 四边形是正方形,∴ 又面,面 ∴面 A到的距离等于B到的距离.即B到面的距离为. 在直角梯形中, ∴ ∴, 在直角梯形中, 可得在等腰中,, ∴, 设点D到平面的距离为d, ,即, 点D到平面的距离为. 【点睛】本题主要考查了证明线线垂直以及求点到平面的距离,属于中档题. 20.已知椭圆的长轴长是短轴长的2倍,且过点. (1)求椭圆的标准方程; (2)直线交椭圆于两点,若点始终在以为直径的圆内,求实数的取值范围. 【答案】(1);(2). 【解析】 【分析】 (1)题设条件为易得椭圆方程; (2)设,直线方程与椭圆方程联立,消元得一元二次方程,由韦达定理可得,注意到直线恒过定点,此为椭圆的左顶点,因此有,,这样可得出点坐标,点始终在以为直径的圆内,则,由此可得的范围. 【详解】(1)由题意知,, 椭圆的标准方程为:. (2)设联立,消去,得: 依题意:直线恒过点,此点为椭圆的左顶点,所以① , 由(*)式,②,得 ③ ,由①②③,, 由点B在以PQ为直径圆内,得为钝角或平角,即. .即 整理得,解得. 【点睛】本题考查椭圆标准方程,考查直线与椭圆相交中的范围问题.由于直线过定点是椭圆左顶点,即其中一个交点已知了,因此可求出另一交点坐标,利用求得结论.本题属于中档题.考查学生的运算求解能力. 21.已知函数. (1)若曲线与直线相切,求实数的值; (2)若不等式在定义域内恒成立,求实数的取值范围. 【答案】(1)1;(2). 【解析】 分析:(1)求导,利用导数的几何意义进行求解;(2)分离参数,将不等式恒成立问题转化为求函数的最值问题,再求导,通过导数的符号变化确定函数的单调性,进而求出极值和最值. 详解:(1), 设切点的横坐标为,由题意得, 解得,, 所以实数的值为1. (2)由题意,在定义域内恒成立, 得在定义域内恒成立, 令, 则, 再令,则, 即在上单调递减,又, 所以当时,,从而,在上单调递增; 当时,,从而,在上单调递减; 所以在处取得最大值, 所以实数的取值范围是. 点睛:1.在处理曲线的切线时,要注意区分“在某点的切线”和“过某点的切线”,前者的点一定为切点,但后者的点不一定在曲线上,且也不一定为切点; 2.在处理含参数的不等式恒成立问题时,往往分离参数,将不等式恒成立问题转化为求函数的最值问题,再利用“恒成立”进行处理. (二)选考题:共10分.请考生在第22、23两题中任选一题做答,如果多做,则按所做的第一题记分. [选修4-4:坐标系与参数方程] 22.在平面直角坐标系中,以坐标原点为极点,轴正半轴为极轴建立极坐标系,直线的极坐标方程为,曲线的极坐标方程为. (1)写出直线和曲线的直角坐标方程; (2)已知点,若直线与曲线交于两点,中点为M,求的值. 【答案】(1)..(2) 【解析】 【分析】 (1)直接利用极坐标和参数方程公式计算得到答案. (2)设直线的参数方程为,代入方程得到,,代入计算得到答案. 【详解】(1)直线,故, 即直线的直角坐标方程为. 因为曲线,则曲线的直角坐标方程为, 即. (2)设直线的参数方程为(为参数), 将其代入曲线的直角坐标系方程得. 设,对应的参数分别为,,则,, 所以M对应的参数,故. 【点睛】本题考查了参数方程和极坐标方程,意在考查学生的计算能力和转化能力. [选修4-5:不等式选讲] 23.已知函数. (1)求不等式的解集; (2)若,使得恒成立,求的取值范围. 【答案】(1) .(2) . 【解析】 【分析】 (1)先由题意得,再分别讨论,,三种情况,即可得出结果; (2)先由含绝对值不等式的性质,得到,再由题意,可得,求解,即可得出结果. 【详解】(1)不等式 可化为, 当时, ,,所以无解; 当时, 所以; 当时,, ,所以, 综上,不等式的解集是. (2)因为 又,使得 恒成立,则, ,解得. 所以的取值范围为. 【点睛】本题主要考查含绝对值的不等式,熟记分类讨论的思想,以及绝对值不等式的性质即可,属于常考题型.查看更多