浙江省衢州市2019-2020学年高二下学期期末教学质量检测数学试题

浙江省衢州市2019-2020学年高二下学期期末教学质量检测数学试题

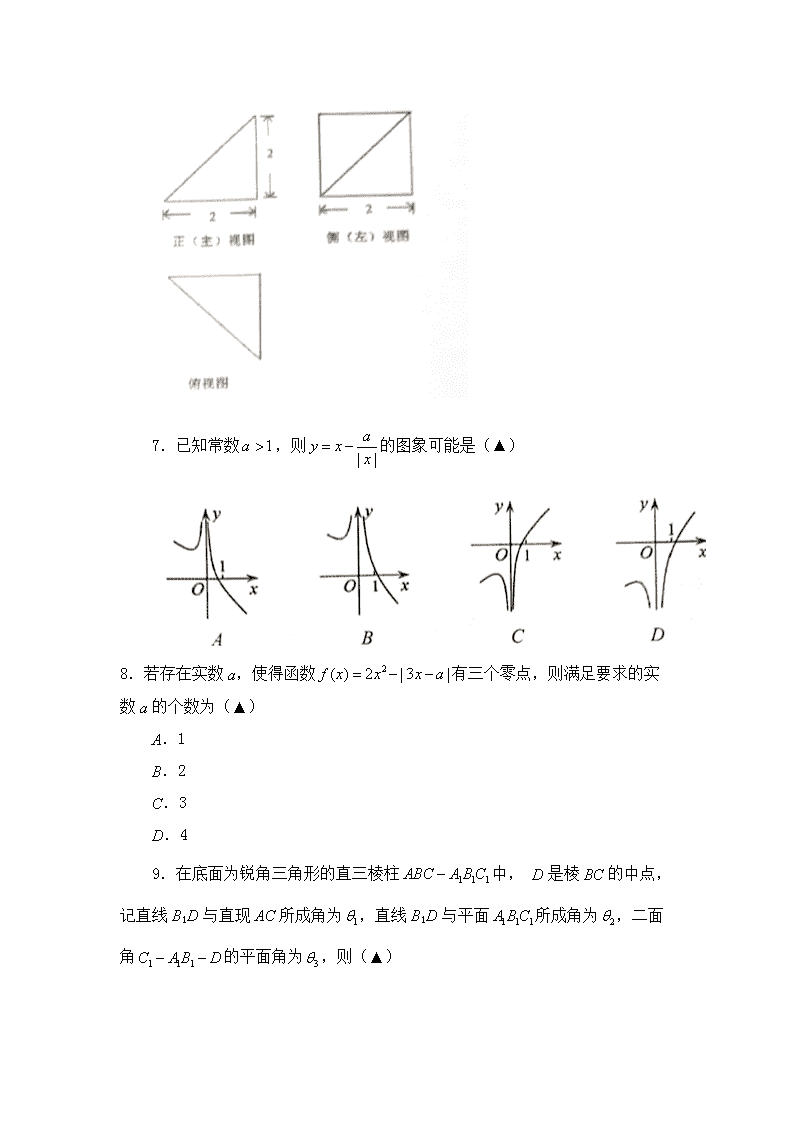
衢州市2020年6月高二年级教学质量检测试卷 数学 一、选择题： （本大题共10小题，每题4分，共40分，每个小题只有一个选项符合题意，多选、不选均不给分．）‎ ‎1．已知集合，则A∩B＝（▲）‎ ‎2．双曲线的渐近线方程为（▲）‎ ‎3．“x＜3”是“”的（▲）‎ A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 ‎4．将函数y＝sin3x的图象向右平移个单位长度后，所得函数图象的解析式为（▲）‎ ‎5．已知变量x，y满足约束条件，则z＝2x＋y的最小值为（▲）‎ A．14 B．8 C．6 D．4‎ ‎6．某四棱锥的三视图如右图所示，则该四棱锥的表面积为（▲）‎ ‎7．已知常数，则的图象可能是（▲）‎ ‎8．若存在实数a，使得函数有三个零点，则满足要求的实数a的个数为（▲）‎ A．1‎ B．2‎ C．3‎ D．4‎ ‎9．在底面为锐角三角形的直三棱柱中， D是棱BC的中点，记直线B1D与直现AC所成角为，直线B1D与平面所成角为，二面角的平面角为，则（▲）‎ ‎10．已知数列中， ，若对于任意的，不等式恒成立，则实数t的取值范围为（▲）‎ 二、填空题： （本大题共7小题，多空题每空3分，单空题每题4分，共36分．）‎ ‎11．直线的斜率为________，倾斜角为________‎ ‎12．已知向量 ，若，则m＝________；若，则m＝________‎ ‎13．十六、十七世纪之交，随着天文、航海、工程、贸易及军事的发展，改进数字计算方法成了当务之急，约翰·纳皮尔正是在研究天文学的过程中，为了简化其中的计算而发明了对数，后来天才数学家欧拉发现了对数与指数的关系，即．现已知，则________，‎ ‎________‎ ‎14．已知△ABC中， AB＝BC＝4， AC＝2，点D为AB延长线上一点， BD＝2，连接CD，则CD＝ ________，△BCD的面积为________‎ ‎15．已知椭圆上有一点，F为右焦点， B为上顶点， O为坐标原点，且 ，则椭圆C的离心率为________‎ ‎16．已知且， 则的最小值为________‎ ‎17．当时，不等式恒成立，则a的取值范围是________‎ 三、解答题： （本大题共5小题，共74分，解答应写出文字说明、证明过程或演算步骤．）‎ ‎18． （本题满分14分）‎ 已知角α的顶点与原点O重合，始边与 x轴的非负半轴重合，它的终边过点P(－4，3)．‎ ‎(1)求cosα的值； (2)若角β满足sin(α－β)＝2，求sinβ的值．‎ ‎19． （本题满分15分）‎ 如图，在三棱锥P—ABC中， PA⊥平面ABC， AC ⊥ BC，D为PC中点，E为AD中点，PA＝AC＝2，BC＝1．‎ ‎（1）求证： AD⊥平面PBC：‎ ‎(2)求PE与平面ABD所成角的正弦值．‎ ‎20．（本题满分15分）设数列的前n项和为 ‎（1）试求a1的值及数列的通项公式；‎ ‎(2)数列满足：，记数列的前n项和为．求证： ．‎ ‎21． （本题满分15分）‎ 如图，抛物线的焦点为F(1，0)， E是抛物线的准线与x轴的交点，直线AB经过焦点F且与抛物线交于A，B两点，直线AE， BE分别交y轴于M， N两点，记△ABE，△MNE的面积分别为．‎ ‎（1）求抛物线C的标准方程；‎ ‎（2）是否为定值？若是，求出该定值；若不是，请说明理由；‎ ‎（3）求的最小值．‎ ‎22． （本题满分15分）‎ 已知函数．‎ ‎(1)若a＝0，求函数f(x)的零点；‎ ‎（2）若不存在相异实数，使得成立。求实数a的取值范围；‎ ‎（3）若对任意实数a，总存在实数，使得成立，求实数k的最大值.‎