2019届二轮复习　平面向量、复数学案（全国通用）

2019届二轮复习　平面向量、复数学案（全国通用）

‎2019届二轮复习 　平面向量、复数 学案（全国通用）‎ 命 题 者 说 考 题 统 计 考 情 点 击 ‎2018·全国卷Ⅰ·T1·复数的运算 ‎2018·全国卷Ⅰ·T6·平面向量的线性运算 ‎2018·全国卷Ⅱ·T1·复数的运算 ‎2018·全国卷Ⅱ·T4·平面向量的数量积运算 ‎2018·全国卷Ⅲ·T2·复数的运算 ‎2018·全国卷Ⅲ·T13·平面向量的坐标运算 ‎　　高考对本部分内容的考查主要有以下几方面：①平面向量的运算。包括向量的线性运算及几何意义，坐标运算，利用数量积运算解决模、夹角、垂直的问题，常与函数、不等式、三角函数、解析几何等知识进行简单的结合；②复数的运算。包括复数的概念、几何意义及四则运算。以上考点难度不高，属送分题，只要掌握基础知识就能得满分。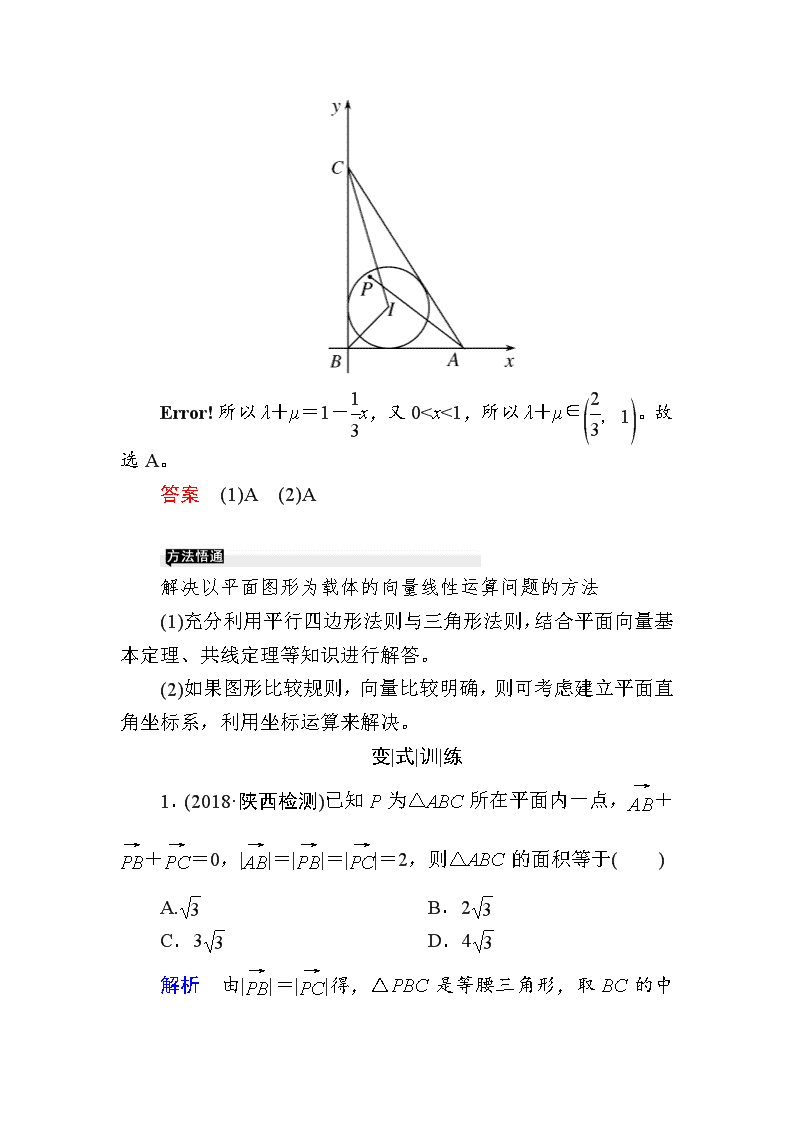‎ 考向一 平面向量 微考向1：平面向量的线性运算 ‎【例1】　(1)(2018·全国卷Ⅰ)在△ABC中，AD为BC边上的中线，E为AD的中点，则＝(　　)‎ A.－ B.－ C.＋ D.＋ ‎(2)(2018·重庆调研)已知Rt△ABC中，AB＝3，BC＝4，AC＝5，I是△ABC的内心，P是△IBC内部(不含边界)的动点，若＝λ＋μ(λ，μ∈R)，则λ＋μ的取值范围是(　　)‎ A. B. C. D．(2,3)‎ 解析　(1)解法一：如图所示，＝＋＝＋＝×(＋)＋(－)＝－，故选A。‎ 解法二：＝－＝－＝－××(＋)＝－，故选A。‎ ‎(2)以B为原点，BA，BC所在直线分别为x，y轴建立如图所示的平面直角坐标系，则B(0,0)，A(3,0)，C(0,4)。设△ABC的内切圆的半径为r，因为I是△ABC的内心，所以(5＋3＋4)×r＝4×3，解得r＝1，所以I(1,1)。设P(x，y)，因为点P在△IBC内部(不含边界)，所以00)，则B(m,0)，C，D。因为E是CD的中点，所以E。所以＝，＝。由·＝1可得＋＝1，即2m2－m＝0。所以m＝0(舍去)或m＝。故AB的长为。‎ 答案　(1)B　(2)3　(3) 解决以平面图形为载体的向量数量积问题的方法 ‎(1)选择平面图形中的模与夹角确定的向量作为一组基底，用该基底表示构成数量积的两个向量，结合向量数量积运算律求解。‎ ‎(2)若已知图形中有明显的适合建立直角坐标系的条件，可建立直角坐标系将向量数量积运算转化为代数运算来解决。 ‎ 变|式|训|练 ‎1．平面向量a与b的夹角为45°，a＝(1,1)，|b|＝2，则|3a＋b|＝(　　)‎ A．13＋6 B．2 C. D. 解析　依题意得|a|＝，a·b＝×2×cos45°＝2，则|3a＋b|＝＝＝＝。故选D。‎ 答案　D ‎2．已知菱形ABCD的边长为2，∠BAD＝120°，点E，F 分别在边BC，DC上，BC＝3BE，DC＝λDF 。若·＝1，则λ的值为________。‎ 解析　解法一：如图，由题意可得·＝||·||cos120°＝2×2×＝－2。在菱形ABCD中，易知＝，＝，所以＝＋＝＋，＝＋＝＋，·＝·＝＋－2＝1，解得λ＝2。‎ 解法二：以A为原点建立直角坐标系如图，则A(0,0)，B(2,0)，C(1，)，D(－1，)，E，设F (x0，)，则·＝·(x0，)＝1，则x0＋1＝1，则x0＝0，所以F 为DC中点，所以DC＝2DF ，即λ＝2。‎ 答案　2‎ 微考向3：平面向量的最值问题 ‎【例3】　(2018·浙江高考)已知a，b，e是平面向量，e是单位向量。若非零向量a与e的夹角为，向量b满足b2－4e·b＋3＝0，则|a－b|的最小值是(　　)‎ A．－1 B．＋1‎ C．2 D．2－ 解析　解法一：设O为坐标原点，a＝，b＝＝(x，y)，e＝(1,0)，由b2－4e·b＋3＝0得x2＋y2－4x＋3＝0，即(x－2)2＋y2＝1，所以点B的轨迹是以C(2,0)为圆心，1为半径的圆。因为a与e的夹角为，所以不妨令点A在射线y＝x(x>0)上，如图，数形结合可知|a－b|min＝||－||＝－1。故选A。‎ 解法二：由b2－4e·b＋3＝0得b2－4e·b＋3e2＝(b－e)·(b－3e)＝0。设b＝，e＝，3e＝，所以b－e＝，b－3e＝，所以·＝0，取EF 的中点为C，则B在以C为圆心，EF 为直径的圆上，如图。设a＝，作射线OA，使得∠AOE＝，所以|a－b|＝|(a－2e)＋(2e－b)|≥|a－2e|－|2e－b|＝||－||≥－1。故选A。‎ 答案　A 平面向量的最值问题的两种解法 ‎(1)坐标法：建立平面直角坐标系，计算有关向量的坐标，利用向量的坐标计算。‎ ‎(2)几何法：根据向量的几何意义构造图形，通过分析图形得出结论。 ‎ 变|式|训|练 已知A，B，C是圆O：x2＋y2＝1上的动点，且AC⊥BC，若点M的坐标是(1,1)，则|＋＋|的最大值为(　　)‎ A．3 B．4‎ C．3－1 D．3＋1‎ 解析　解法一：因为A，B，C是圆O：x2＋y2＝1上的动点，且AC⊥BC，所以设A(cosθ，sinθ)，B(－cosθ，－sinθ)，C(cosα，sinα)，其中0≤θ<2π，0≤α<2π，因为M(1,1)，所以＋＋＝(cosθ－1，sinθ－1)＋(－cosθ－1，－sinθ－1)＋(cosα－1，sinα－1)＝(cosα－3，sinα－3)，所以|＋＋|‎ ‎＝ ‎＝ ‎＝，当且仅当sin＝－1时，|＋＋|取得最大值，最大值为＝3＋1。故选D。‎ 解法二：连接AB，因为AC⊥BC，所以AB为圆O的直径，所以＋＝2，所以|＋＋|＝|2＋|≤|2|＋||＝2＋||，易知点M与圆上动点C的距离的最大值为＋1，所以||≤＋1，所以|＋＋|≤3＋1。故选D。‎ 答案　D 考向二 复数的运算 ‎【例4】　(1)(2018·全国卷Ⅱ)＝(　　)‎ A．－－i B．－＋i C．－－i D．－＋i ‎(2)(2018·北京高考)在复平面内，复数的共轭复数对应的点位于(　　)‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 解析　(1)因为＝＝＝－＋i。故选D。‎ ‎(2)＝＝＋i，其共轭复数为－i，对应的点为。故选D。‎ 答案　(1)D　(2)D 复数问题的解题思路 ‎(1)以复数的基本概念、几何意义、相等的条件为基础，结合四则运算，利用复数的代数形式列方程或方程组解决问题。‎ ‎(2)若与其他知识结合考查，则要借助其他的相关知识解决问题。 ‎ 变|式|训|练 ‎1．设i是虚数单位，若复数a＋(a∈R)是纯虚数，则a＝(　　)‎ A．－1 B．1‎ C．－2 D．2‎ 解析　因为a＋＝a＋＝a－2＋i为纯虚数，所以a－2＝0，得a＝2。故选D。‎ 答案　D ‎2．复数z＝(i为虚数单位)在复平面内对应点的坐标为(　　)‎ A．(3,3) B．(－1,3)‎ C．(3，－1) D．(2,4)‎ 解析　因为z＝＝＝＝－1＋3i，所以其在复平面内对应的点的坐标为(－1,3)。故选B。‎ 答案　B ‎3．复数z满足＝i(i为虚数单位)，则＝(　　)‎ A．1＋i　　　B．1－i C.　　　D. 解析　因为＝i，所以z＝(z－i)i＝zi＋1，z＝＝，＝，故选D。‎ 答案　D ‎1．(考向一)(2018·河北、河南、山西联考)如图，在等边△ABC中，O为△ABC的重心，点D为BC边上靠近B点的四等分点，若＝x＋y，则x＋y＝(　　)‎ A. B. C. D. 解析　设点E为BC的中点，连接AE，可知O在AE上，由＝＋＝＋＝(＋)＋(－)＝－，故x＝，y＝－，x＋y＝。故选B。‎ 答案　B ‎2．(考向一)(2018·天津高考)如图，在平面四边形ABCD中，AB⊥BC，AD⊥CD，∠BAD＝120°，AB＝AD＝1。若点E为边CD上的动点，则·的最小值为(　　)‎ A． B． C． D．3‎ 解析　解法一：如图，以D为原点DA所在直线为x轴，DC所在直线为y轴，建立平面直角坐标系，则A(1,0)，B，C(0，)，令E(0，t)，t∈[0，]，所以·＝(－1，t)· ‎＝t2－t＋，因为t∈[0，]，所以当t＝－＝时，·取得最小值，(·)min＝－×＋＝。故选A。‎ 解法二：令＝λ(0≤λ≤1)，由已知可得DC＝，因为＝＋λ，所以＝＋＝＋＋λ，所以·＝(＋λ)·(＋＋λ)＝·＋2＋λ·＋2＝3λ2－λ＋。当λ＝－＝时，·取得最小值。故选A。‎ 答案　A ‎3．(考向二)(2018·株洲二模)设i为虚数单位，1－i＝，则实数a＝(　　)‎ A．2 B．1‎ C．0 D．－1‎ 解析　因为1－i＝，所以2＋ai＝(1－i)(1＋i)＝2，所以a＝0。故选C。‎ 答案　C ‎4．(考向二)已知复数z的共轭复数为，若(1－2i)＝5－i(i为虚数单位)，则在复平面内，复数z对应的点位于(　　)‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 解析　依题意，设z＝a＋bi(a，b∈R)，则＋＝2a＋bi，故2a＋bi＝＝1＋i，故a＝，b＝，则在复平面内，复数z对应的点为，位于第一象限。故选A。‎ 答案　A