江西省2020届高三上学期模拟检测数学（文）试卷

江西省2020届高三上学期模拟检测数学（文）试卷

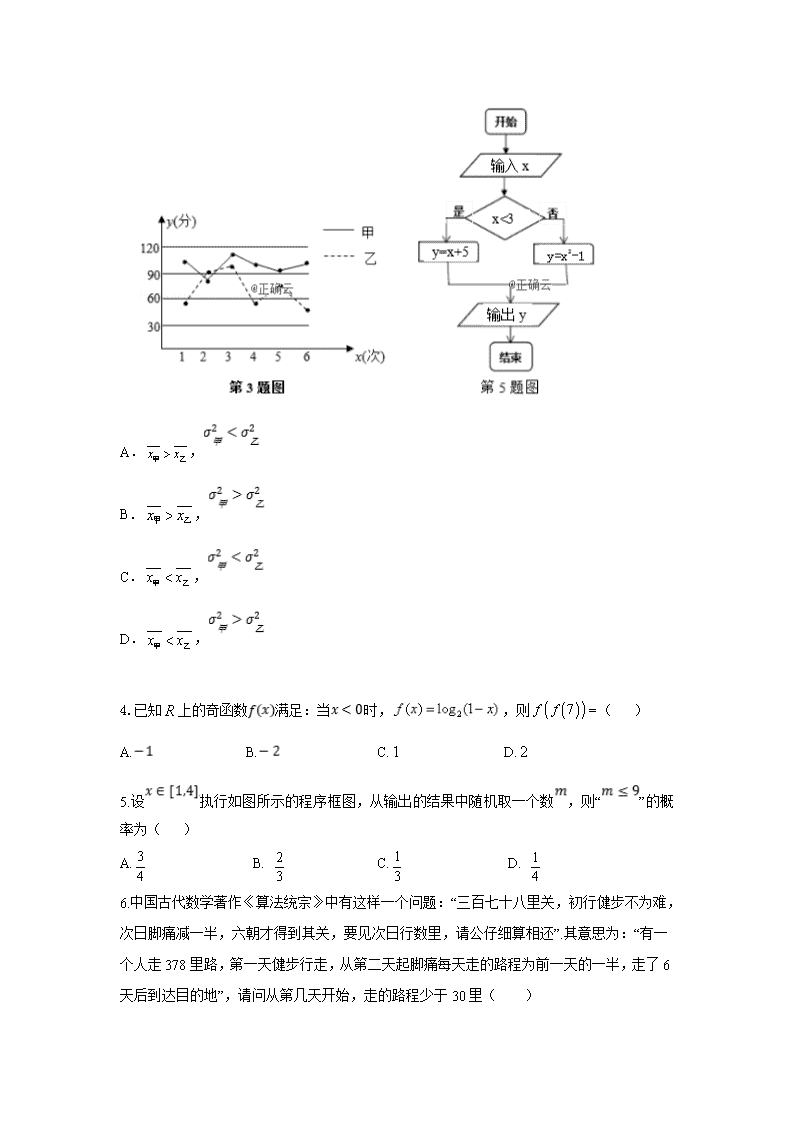
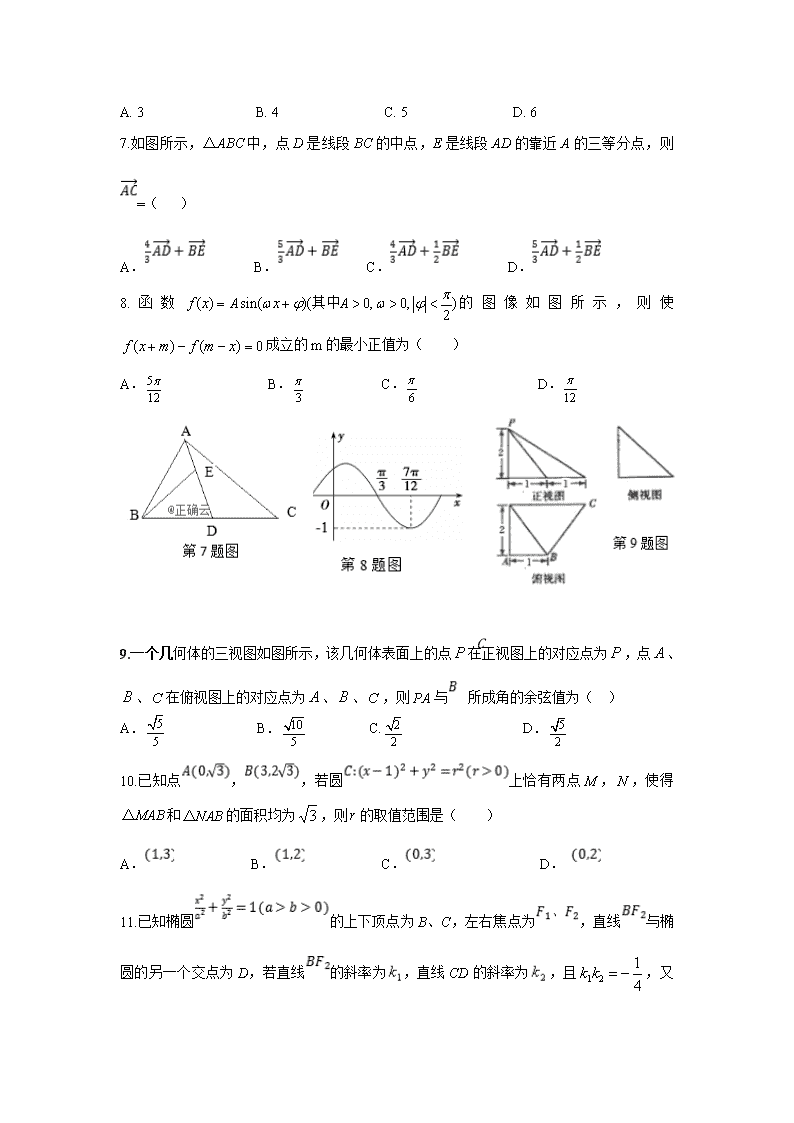
数学（文科）试卷 考试时间：120分钟 本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。共150分。‎ 考生注意：‎ 1. 答题前，考生将自己的准考证号、姓名填写在答题卡上。考生要认真核对答题卡上粘贴的条形码的“准考证号、姓名、考试科目”与考生本人准考证号、姓名是否一致。‎ 2. 第Ⅰ卷每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑。第Ⅱ卷用黑色墨水签字笔在答题卡上书写作答，在试卷上作答，答案无效。‎ 3. 考试结束，监考员将试题卷、答题卡一并回收。‎ 第Ⅰ卷（选择题）‎ 一．选择题：共12小题，满分60分，每小题5分。‎ ‎1.已知集合，,则 ( )‎ A. B. {3} C.{2,3} D. ‎ ‎2.已知是两个命题，那么“是真命题”是“是假命题”的（ ）‎ A．既不充分也不必要条件 B．充分必要条件 ‎ C．充分不必要条件 D．必要不充分条件 ‎3．甲乙两名同学6次考试的成绩统计如图，甲乙两组数据的平均数分别为,方差分别 为，则（　　）‎ A．， ‎ B．，‎ C．，‎ D．， ‎ ‎4.已知上的奇函数满足：当时，，则（ ）‎ A. B. C. D.‎ ‎5.设执行如图所示的程序框图，从输出的结果中随机取一个数，则“”的概率为（ ）‎ A. B. C. D. ‎ ‎6.中国古代数学著作《算法统宗》中有这样一个问题：“三百七十八里关，初行健步不为难，次日脚痛减一半，六朝才得到其关，要见次日行数里，请公仔细算相还”.其意思为：“有一个人走378里路，第一天健步行走，从第二天起脚痛每天走的路程为前一天的一半，走了6天后到达目的地”，请问从第几天开始，走的路程少于30里（ ）‎ A. 3 B. 4 C. 5 D. 6‎ ‎7.如图所示，△ABC中，点D是线段BC的中点，E是线段AD的靠近A的三等分点，则=（ ）‎ A． B． C． D． ‎ ‎8.函数的图像如图所示，则使成立的m的最小正值为（ ）‎ A． B． C． D．‎ ‎9.一个几何体的三视图如图所示，该几何体表面上的点在正视图上的对应点为，点、、在俯视图上的对应点为、、，则PA与C所成角的余弦值为（ ） ‎ A． B． C. D． ‎ ‎10.已知点，，若圆上恰有两点，，使得和的面积均为，则的取值范围是（ ）‎ A． B． C． D． ‎ ‎11.已知椭圆的上下顶点为B、C，左右焦点为，直线与椭圆的另一个交点为D，若直线的斜率为，直线CD的斜率为，且，又 的周长为8，则的面积为（ ）．‎ A．1 B． C． D．2‎ 12. 定义在R上的连续可导函数f（x），其导函数记为，满足f（x）+f（2﹣x）＝（x﹣1）2，‎ 且当x1时，恒有 +2＜x．若，则实数m的取值范围是（　　）‎ A．（﹣∞，1] B． C．[1，+∞） D．‎ 第Ⅱ卷（非选择题）‎ 二．填空题：共4小题，满分20分，每小题5分。‎ ‎13.若复数满足（其中为虚数单位），则等于______．‎ ‎14.设x，y满足约束条件，若，则z的最大值为______．‎ ‎15.数列满足，其前项和为.若恒成立，则M的最小值 为_____．‎ ‎16.体积为的三棱锥P-ABC的顶点都在球O的球面上，PC平面ABC,PC=4,,则球O的表面积的最小值为 ． ‎ 三．解答题：共70分。解答应写出文字说明、证明过程或演算步骤。第17~21题为必考题，每个试题考生都必须作答。第22~23题为选考题，考生根据要求作答。‎ ‎17．（12分）已知分别为三个内角A,B,C的对边，且.‎ ‎（1）求角A的大小；‎ ‎（2）若AD是BC边上的中线，b＝3，AD＝，求△ABC的面积．‎ ‎18．（12分）2020年开始，国家逐步推行全新的高考制度.新高考不再分文理科，采用3+3‎ 模式，其中语文、数学、外语三科为必考科目，满分各150分，另外考生还要依据想考取的高校及专业的要求，结合自己的兴趣爱好等因素，在思想政治、历史、地理、物理、化学、生物6门科目中自选3门参加考试（6选3），每科目满分100分.为了应对新高考，某高中从高一年级1500名学生（其中男生900人，女生600 人）中，采用分层抽样的方法从中抽取名学生进行调查.‎ ‎（1）已知抽取的名学生中含女生20人，求的值及抽取到的男生人数；‎ ‎（2）学校计划在高一上学期开设选修中的“物理”和“地理”两个科目，为了了解学生对这两个科目的选课情况，对在（1）的条件下抽取到的名学生进行问卷调查（假定每名学生在这两个科目中必须选择一个科目且只能选择一个科目），下表是根据调查结果得到的列联表. 请将列联表补充完整，并判断是否有 99%的把握认为选择科目与性别有关？说明你的理由；‎ （3） 在（2）抽取的选择“地理”的学生中按分层抽样再抽取5名，再从这5名学生中抽取2人了解学生对“地理”的选课意向情况，求2人中至少有1名男生的概率.‎ ‎ 附：参考公式及数据 19． ‎（12分）在四棱锥中，AB//CD，，与相交于点，点在线段上，. ‎ ‎（1）求证：∥平面 ‎ ‎（2）若，， ，‎ 求点到平面的距离.‎ ‎20.（12分）在平面直角坐标系xOy中，椭圆C：的离心率为，抛物线E：的焦点是椭圆C的一个顶点．‎ ‎（1）求椭圆C的方程；‎ ‎（2）若过点Q（1,0）的直线与椭圆C交于A，B两点，问是否在x轴上存在一点T，使得∠ATQ=∠BTQ？若存在，求出点T的坐标，若不存在，说明理由．‎ ‎21．（12分）已知函数，‎ ‎（1）若函数的极小值是，求的值；‎ ‎（2）设是函数图象上任意不同的两点，线段的中点为，直线的斜率为.证明：.‎ 选考题共10分。请考生在22、23题中任选一题作答。如果多做，则按所做的第一题计分。‎ ‎22．（10分）选修4-4：坐标系与参数方程 在直角坐标系 xoy 中，曲线 C1 的直角坐标方程为，以坐标原点为极点，以 x 轴正半轴为极轴，建立极坐标系，曲线 C2 的极坐标方程为 ‎ ‎（1）求 C1 的极坐标方程和 C2 的直角坐标方程;‎ ‎（2）已知射线的的直角坐标方程为,若射线与C1，C2 分别交于 A，B 两点，‎ 求的值.‎ ‎23．（10分）选修4-5：不等式选讲 已知函数．‎ ‎（1）当时，解不等式；‎ ‎（2）当时，不等式恒成立，求实数的取值范围．‎ ‎ ‎ 参考答案与试题解析 一． 选择题 BCADC BBDBA CA 二．填空题 ‎13．5 14．3 15． 16．‎ 三．解答题 ‎17,解：（1）由已知及正弦定理得 …………………………2分 ‎，所以，即sin(A+, …………………………4分 因为（），所以，所以A= …………………………6分 ‎（2）以AB，AC为邻边作平行四边形ABEC，在△ACE中，．………………………………………………8分 由余弦定理得AE2＝AC2+CE2﹣2AC•CE•cos120°，又AB＝CE 即：，………………………………10分 解得，AB＝2．故．…………………………12分 ‎18．【解析】（1）由题意得：，解得，男生人数为：50-20=30人．…………2分 ‎（2）列联表为：‎ ‎………………………………3分 ‎ …………………………………………………5分 所以有的把握认为选择科目与性别有关. ……………………………… 6分 ‎ ‎（3）从25个选择地理的学生中分层抽样抽5名，‎ 所以这5名学生中有2名男生，3名女生，………………………………7分 男生编号为1，2，女生编号为a，b，c， 5名学生中再选抽2个，‎ 则所有可能的结果为Ω={ab，ac， a1，a2，bc， b1，b2， c1，c2， 12}，……………9分 至少一名男生的结果为{a1，a2，b1，b2，c1，c2， 12}，‎ 所以2人中至少一名男生的概率为 ……………………………… 12分 ‎19．【解析】解法一：（1）因为,所以即．‎ 因为,所以 , 所以∥,平面，平面 , 所以∥平面，…………………………5分 ‎ ‎(2)因为,所以为等边三角形，所以,‎ 又因为,所以且,所以且又因为所以 …………………………7分 因为平面,所以 作因为,所以 ‎ 所以EH为点到平面的距离. …………………………9分 在中，设边上的高为，则 因为,所以,即点到平面的距离为1 …………12分 解法二、（1）同解法一。‎ ‎（2）因为,所以为等边三角形，所以,‎ 又因为,所以且,所以且又因为所以 …………………………7分 设点到平面的距离为，因为，所以………9分 即 ‎ 因为,，‎ 所以，解得，即点到平面的距离为1。…………12分 ‎20．解：（1）由题意知 椭圆方程为： ………………………… 4分 （2） ‎(1)当直线斜率不存在，显然x轴上任意一点T均成立 ………………………… 5分 ‎（2）当直线斜率存在，设直线斜率为k,假设存在T（t，0）满足∠ATQ=∠BTQ．‎ 设A（x1，y1），B（x2，y2）联立，‎ 得（1+2k2）x2﹣4k2x+2k2﹣8=0，‎ 由韦达定理有①，其中△＞0恒成立， ‎ 由∠ATQ=∠BTQ（显然TA，TB的斜率存在），‎ 故kTA+kTB=0即②，………………………… 7分 由A，B两点在直线y=k（x﹣1）上，‎ 故y1=k（x1﹣1），y2=k（x2﹣1）代入②‎ 得，‎ 即有2x1x2﹣（t+1）（x1+x2）+2t=0③，…………………………9分 将①代入③，即有：‎ ‎④ ‎ 要使得④与k的取值无关，当且仅当“t=8“时成立，综上所述存在T（8，0），使得∠ATQ=∠BTQ．12分 ‎21．解：(1)函数的定义域为，……………………1分 当时，恒大于0，在上递增，无极值 …………………… 2分 当，,,且时，在递减 时，在递增 故在的极小值为= ……………………4分 经检验，使得函数的极小值为成立……………………5分 ‎（2）证明：由已知可得，又，所以。要证，即证………6分 不妨设，即证，即证。……………………8分 设，即证，即证，其中。 ……9分 设，则所以在上单调递增，因此 得证. ……………………12分 ‎22．解： (1)由C1 ：，得，即，所以曲线C1 的极坐标方程为由C2 ：，得，即，所以C2 的直角坐标方程为 …………………………………5分 ‎（2）法一：设直线的倾斜角为，则直线的极坐标方程为 且 代入曲线 C1 的极坐标方程得 将代入曲线 C2 的极坐标方程得 ‎ 所以= ……………………………………10分 ‎ 法二：直线的参数方程为，将的参数方程代入C1 的直角坐标方程得，所以 将的参数方程代入C2 的直角坐标方程得，所以，所以= …………………………………… 10分 ‎23．解：(1)当时,，由解得 ……………………………5分 （2） ‎, ‎ 时，使得 不等式恒成立 ……………………7分 不等式恒成立，‎ ‎， ……………………………9分 又 …………………………… 10分 访问“高中试卷网”——http://sj.fjjy.org