高考文科数学复习备课课件：第八节　函数与方程

高考文科数学复习备课课件：第八节　函数与方程

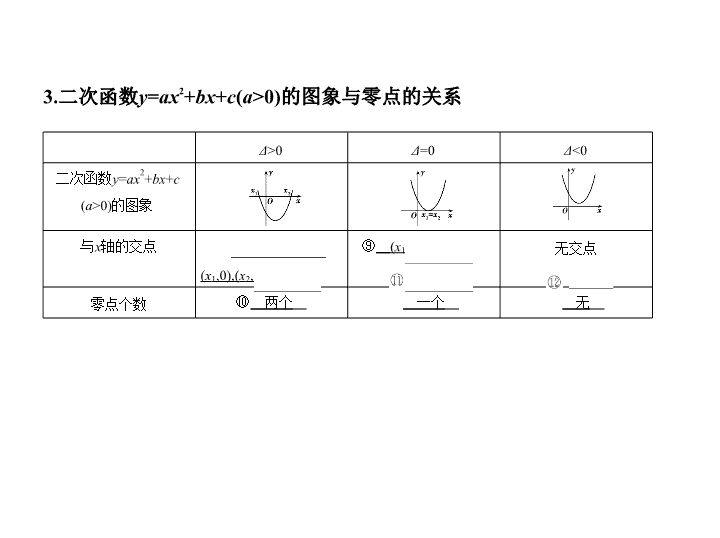
文数 课标 版 第八节　函数与方程 1.函数零点的定义 (1)对于函数 y = f ( x ),把使①      f ( x )=0     的实数 x 叫做函数 y = f ( x )的零点. (2)方程 f ( x )=0有实根 ⇔ 函数 y = f ( x )的图象与②      x 轴     有交点 ⇔ 函数 y = f ( x )有③ 　零点     . 教材研读 2.函数零点的判定(零点存在性定理) 一般地,如果函数 y = f ( x )在区间[ a , b ]上的图象是连续不断的一条曲线,并 且有④      f ( a )· f ( b )<0     ,那么函数 y = f ( x )在区间⑤ 　( a , b )     内有零点,即存 在 c ∈( a , b ),使得⑥      f ( c )=0     ,这个⑦      c      也就是方程 f ( x )=0的根.我们 把这一结论称为零点存在性定理. 3.二次函数 y = ax 2 + bx + c ( a >0)的图象与零点的关系 Δ >0 Δ =0 Δ <0 二次函数 y = ax 2 + bx + c ( a >0)的图象       与 x 轴的交点 ⑧ 　( x 1 ,0),( x 2 ,0)     ⑨ 　( x 1 ,0)     无交点 零点个数 ⑩ 　两个       　一个       　无     4.用二分法求函数 f ( x )零点近似值的步骤 第一步,确定区间[ a , b ],验证        f ( a )· f ( b )<0     ,给定精确度ε. 第二步,求区间( a , b )的中点 x 1 . 第三步,计算        f ( x 1 )     : (i)若        f ( x 1 )=0     ,则 x 1 就是函数的零点; (ii)若        f ( a )· f ( x 1 )<0     ,则令 b = x 1 (此时零点 x 0 ∈( a , x 1 )); (iii)若        f ( x 1 )· f ( b )<0     ,则令 a = x 1 (此时零点 x 0 ∈( x 1 , b )). 第四步,判断是否达到精确度ε:若| a - b |<ε,则得到零点近似值 a (或 b );否则, 重复第二、三、四步.   　　判断下列结论的正误(正确的打“√”,错误的打“ × ”) (1)函数的零点就是函数的图象与 x 轴的交点.   ( × ) (2)函数 y = f ( x )在区间( a , b )内有零点(函数图象连续不间断),则 f ( a )· f ( b )<0.   ( × ) (3)只要函数有零点,我们就可以用二分法求出零点的近似值.   ( × ) (4)二次函数 y = ax 2 + bx + c ( a ≠ 0)在 b 2 -4 ac <0时没有零点.   (√) (5)若函数 f ( x )在( a , b )上单调且 f ( a )· f ( b )<0,则函数 f ( x )在[ a , b ]上有且只有一 个零点.   (√)   1.下列函数图象与 x 轴均有交点,其中不能用二分法求图中函数零点的 是   (　　)   答案     C　对于选项C,由图可知零点附近左右两侧的函数值的符号是 相同的,故不能用二分法求解. 2.已知函数 y = f ( x )的图象是连续曲线,且有如下的对应值表: 则函数 y = f ( x )在区间[1,6]上的零点至少有   (　　) A.2个　    B.3个　    C.4个　    D.5个 答案     B　由零点存在性定理及题中的对应值表可知,函数 f ( x )在区间 (2,3),(3,4),(4,5)内均有零点,所以 y = f ( x )在[1,6]上至少有3个零点.故选B. x 1 2 3 4 5 6 y 124.4 35 -74 14.5 -56.7 -123.6 3.函数 f ( x )=ln x -   的零点所在的大致范围是   (　　) A.(1,2)　    B.(2,3) C.   和(3,4)　    D.(4,+ ∞ ) 答案     B　易知 f ( x )为增函数,由 f (2)=ln 2-1<0, f (3)=ln 3-   >0,得 f (2)· f (3)< 0.故选B. 4.函数 f ( x )=e x +3 x 的零点个数是   (　　) A.0　    B.1　     C.2　    D.3 答案     B　函数 f ( x )=e x +3 x 在R上是增函数, ∵ f (-1)=   -3<0, f (0)=1>0, ∴ f (-1)· f (0)<0, ∴函数 f ( x )有唯一零点,且在(-1,0)内,故选B. 5.函数 y =   - m 有两个零点,则 m 的取值范围是 　　　     . 答案 　(0,1) 解析 　在同一直角坐标系内,画出 y 1 =   和 y 2 = m 的图象,如图所示,由于 原函数有两个零点,故0< m <1.   考点一　函数零点所在区间的判断 典例1 　(1)(2016赣中南五校联考)在下列区间中,函数 f ( x )=3 x - x 2 有零点 的区间是   (　　) A.[0,1]　    B.[1,2]　    C.[-2,-1]　    D.[-1,0] (2)(2016湖南长沙模拟)已知函数 f ( x )=ln x -   的零点为 x 0 ,则 x 0 所在的 区间是   (　　) A.(0,1)　    B.(1,2)　    C.(2,3)　    D.(3,4) 考点突破 ∵ f (-2)=   -4, f (-1)=   -1,∴ f (-2) f (-1)>0, ∵ f (0)=1, f (-1)=   -1,∴ f (0) f (-1)<0, 易知[-1,0]符合条件,故选D. (2)∵ f ( x )=ln x -   在(0,+ ∞ )上是增函数, 答案　 (1)D　(2)C 解析　 (1)∵ f (0)=1, f (1)=2,∴ f (0) f (1)>0, ∵ f (2)=5, f (1)=2,∴ f (2) f (1)>0, 又 f (1)=ln 1-   =ln 1-2<0, f (2)=ln 2-   <0, f (3)=ln 3-   >0, ∴ x 0 ∈(2,3),故选C. 方法技巧 判断函数在某个区间上是否存在零点的方法 (1)解方程,当对应方程易解时,可通过解方程看方程是否有根落在给定 区间上进行判断; (2)利用零点存在性定理进行判断; (3)画出函数图象,通过观察图象与 x 轴在给定区间内是否有交点来判断. 1-1　 函数 f ( x )=   +ln   的零点所在的大致区间为   (　　) A.(1,2)　    B.(2,3) C.(3,4)　    D.(1,2)与(2,3) 答案     B     f ( x )=   +ln   =   -ln( x -1),其在定义域(1,+ ∞ )上是减函数.当1 < x <2时,ln( x -1)<0,   >0,即 f ( x )>0,故函数在(1,2)上没有零点. f (2)=   -ln 1= 1>0, f (3)=   -ln 2=   =   ,因为   =2   ≈ 2.828,所以   >e,故ln e 0, f ( b )<0, f ( c )>0,又函数 f ( x )是二次函数,且图象开口向上,故两个 零点分别在( a , b )和( b , c )内,选A. 考点二　判断函数零点的个数 典例2 　(1)(2016湖北华师一附中3月联考)已知函数 f ( x )=   则函数 g ( x )= f (1- x )-1的零点个数为   (　　) A.1　    B.2　    C.3　    D.4 (2)(2016 江西高安中学等九校联考 ) 定义在 R 上的函数 f ( x ) 满足 f ( x )+ f ( x + 4)=16, 当 x ∈ (0,4] 时 , f ( x )= x 2 -2 x , 则函数 f ( x ) 在 [-4,2 016] 上的零点个数是   ( 　　 ) A.504 　     B.505 　     C.1 008 　     D.1 009 答案 　(1)C　(2)B 解析　 (1) g ( x )= f (1- x )-1 =   ⇒ g ( x )=   当 x ≥ 1时,函数 g ( x )有1个零点;当 x <1时,函数 g ( x )有2个零点,所以函数 g ( x )的零点个数为3,故选C. (2)∵ f ( x )+ f ( x +4)=16,∴ f ( x +4)+ f ( x +8)=16, ∴ f ( x )= f ( x +8),∴函数 f ( x )是R上周期为8的函数;又 f (2)= f (4)=0,2 020=8 × 25 2+4, f (2)= f (10)= f (18)= … = f (8 × 251+2), f (-4)= f (4)= … = f (8 × 251+4),故函数 f ( x )在[-4,2 016]上的零点个数是251+1+251+2=505,故选B. 方法技巧 1.判断零点个数的方法:①直接求零点:令 f ( x )=0,求解方程,有几个解就有 几个零点;②利用零点存在性定理:利用定理不仅要求函数图象在[ a , b ] 上是连续的曲线,且 f ( a )· f ( b )<0,还必须结合函数的图象和性质才能确定 函数有几个零点;③画两个相应函数的图象,有几个交点,就有几个零点. 2.函数的零点、方程的根、函数图象与 x 轴的交点的横坐标,实质是同 一个问题的三种不同表达形式,方程根的个数就是函数零点的个数,即 该函数的图象与 x 轴的交点的个数. 2-1 　函数 f ( x )=2 x |log 0.5 x |-1的零点个数为   (　　) A.1　    B.2　    C.3　    D.4 答案     B　易知函数 f ( x )=2 x |log 0.5 x |-1的零点个数 ⇔ 方程|log 0.5 x |=   =   的根的个数 ⇔ 函数 y 1 =|log 0.5 x |与 y 2 =   的图象的交点个数.作出两个函 数的图象如图所示,由图可知两个函数图象有两个交点,故选B.   2-2 　已知函数 f ( x )=sgn( x -1)-ln x ,且sgn( x )=   则函数 f ( x )零点的个 数为 　　　     . 答案 　3 解析 　依题意得,当 x -1>0,即 x >1时, f ( x )=1-ln x ,此时,令 f ( x )=0,得 x =e>1;当 x -1=0,即 x =1时, f ( x )=0-ln 1=0;当 x -1<0,即 x <1时, f ( x )=-1-ln x ,此时,令 f ( x )= 0,得 x =   <1.因此,函数 f ( x )的零点个数为3. 考点三　函数零点的应用 命题角度一　利用函数的零点比较大小 典例3 　设函数 f ( x )=e x + x -2, g ( x )=ln x + x 2 -3.若实数 a , b 满足 f ( a )=0, g ( b )=0,则   (　　) A. g ( a )<0< f ( b )　    B. f ( b )<0< g ( a ) C.0< g ( a )< f ( b )　    D. f ( b )< g ( a )<0 答案     A 解析 　∵ f ( x )=e x + x -2, ∴ f '( x )=e x +1>0, 则 f ( x )在R上为增函数, 又 f (0)=e 0 -2<0, f (1)=e-1>0,且 f ( a )=0, ∴0< a <1. ∵ g ( x )=ln x + x 2 -3, ∴ g '( x )=   +2 x . 当 x ∈(0,+ ∞ )时, g '( x )>0, ∴ g ( x )在(0,+ ∞ )上为增函数, 又 g (1)=ln 1-2=-2<0, g (2)=ln 2+1>0,且 g ( b )=0, ∴1< b <2,∴ a < b , ∴   故选A. 3-1　函数 f ( x )=2 x -   - a 的一个零点在区间(1,2)内,则实数 a 的取值范围是   (　　) A.(1,3)　    B.(1,2)　     C.(0,3)　    D.(0,2) 答案     C　由条件可知 f (1) f (2)<0, 即(2-2- a )(4-1- a )<0, 即 a ( a -3)<0,解得0< a <3,故选C. 典例4 　(1)(2017山西大同模拟)已知函数 f ( x )=|log 2 x |, g ( x )=   若方程 f ( x )- g ( x )=1在[ a ,+ ∞ )上有三个实根,则正实数 a 的 取值范围是 　　　     . (2)(2017山东临沂期中)已知函数 f ( x )=   若函数 y = f ( x )- b ,当 b ∈(0,1)时总有三个零点,则 a 的取值范围是 　　　　　     . 答案 　(1)   　(2)(- ∞ ,-2] 解析 　(1)∵ f ( x )- g ( x )=1在[ a ,+ ∞ )上有三个实根, ∴ f ( x )-1= g ( x )在[ a ,+ ∞ )上有三个实根, ∴函数 y = f ( x )-1与 y = g ( x )的图象在 x ∈[ a ,+ ∞ )上有三个交点, 命题角度二　利用函数的零点求参数的范围 作出 y = f ( x )-1和 y = g ( x )的图象,如图.   从图象可知, a ≤ x A , 令 f ( x )-1=|log 2 x |-1=0, 得 x =   或 x =2,故 x A =   , ∴ a ≤   , 又∵ a 为正实数, ∴0< a ≤   . (2)函数 y = f ( x )- b ,当 b ∈(0,1)时总有三个零点, 即函数 y = f ( x )与 y = b 的图象当 b ∈(0,1)时总有三个交点,作出两个函数的 图象,如图.   由图可得   解得 a ≤ -2. 方法技巧 已知函数有零点(或方程有根),求参数取值范围的常用方法 (1)直接法:直接根据题设条件构建关于参数的不等式,再通过解不等式 确定参数范围; (2)分离参数法:将参数分离,转化成求函数值域问题加以解决; (3)数形结合法:先对函数解析式(或方程)变形,在同一平面直角坐标系 中画出两个相应函数的图象,然后数形结合求解.