高中数学选修2-2教案第三章 1_1
1.1 导数与函数的单调性
明目标、知重点
1.结合实例,直观探索并掌握函数的单调性与导数的关系.
2.能利用导数判断函数的单调性.
3.会求函数的单调区间(其中多项式函数一般不超过三次).
导数与函数单调性的关系
(1)一般地,在区间(a,b)内
导数
函数的单调性
f′(x)>0
单调递增
f′(x)<0
单调递减
f′(x)=0
常数函数
(2)若函数f(x)在(a,b)内存在导函数且单调递增(递减),则对一切x∈(a,b)都有f′(x)≥0(f′(x)≤0),且在(a,b)任一子区间内f′(x)不恒为零.
(3)利用导数讨论函数的单调性或求单调区间时,首先要确定函数的定义域,解决问题的过程只能在定义域内进行,即单调区间一定是定义域的子区间.当函数y=f(x)有多个单调区间时,不能用“∪”或“或”把单调区间连起来,而应用“,”或“和”连起来.
探究点一 函数的单调性与导函数正负的关系
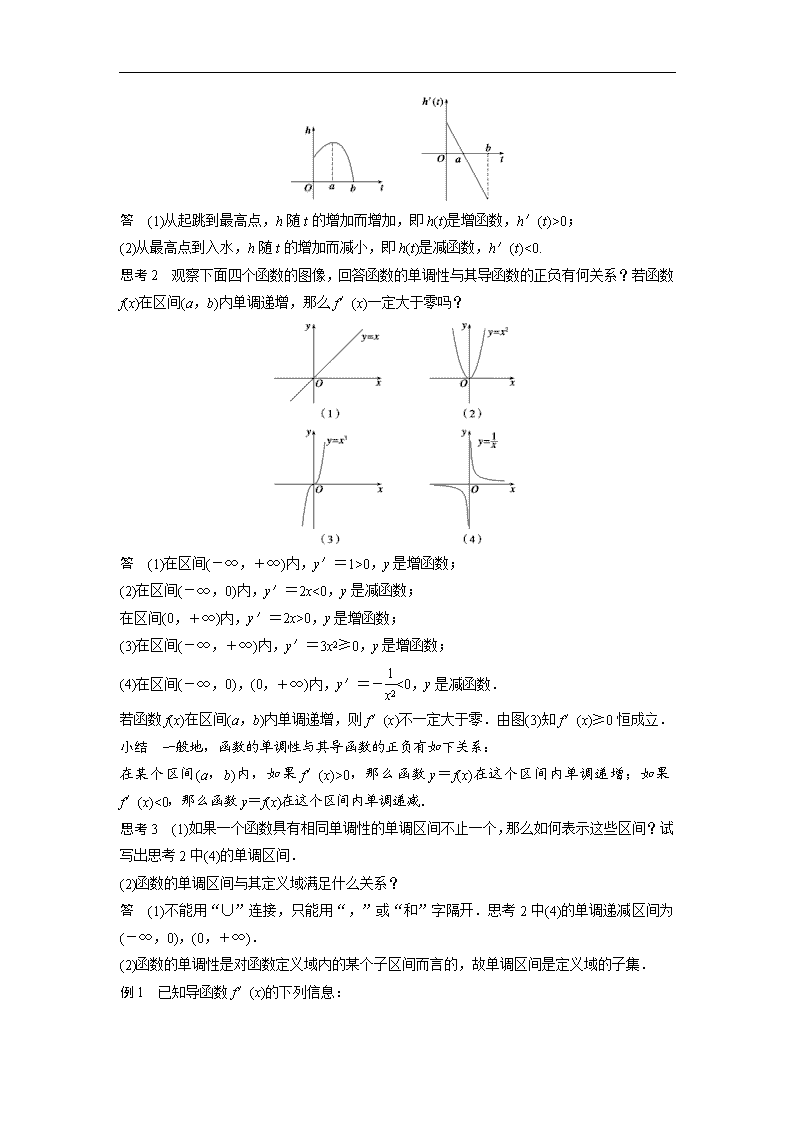
思考1 观察高台跳水运动员的高度h随时间t变化的函数h(t)=-4.9t2+6.5t+10的图像,及运动员的速度v随时间t变化的函数v(t)=h′(t)=-9.8t+6.5的图像,思考运动员从起跳到最高点,从最高点到入水的运动状态有什么区别.
答 (1)从起跳到最高点,h随t的增加而增加,即h(t)是增函数,h′(t)>0;
(2)从最高点到入水,h随t的增加而减小,即h(t)是减函数,h′(t)<0.
思考2 观察下面四个函数的图像,回答函数的单调性与其导函数的正负有何关系?若函数f(x)在区间(a,b)内单调递增,那么f′(x)一定大于零吗?
答 (1)在区间(-∞,+∞)内,y′=1>0,y是增函数;
(2)在区间(-∞,0)内,y′=2x<0,y是减函数;
在区间(0,+∞)内,y′=2x>0,y是增函数;
(3)在区间(-∞,+∞)内,y′=3x2≥0,y是增函数;
(4)在区间(-∞,0),(0,+∞)内,y′=-<0,y是减函数.
若函数f(x)在区间(a,b)内单调递增,则f′(x)不一定大于零.由图(3)知f′(x)≥0恒成立.
小结 一般地,函数的单调性与其导函数的正负有如下关系:
在某个区间(a,b)内,如果f′(x)>0,那么函数y=f(x)在这个区间内单调递增;如果f′(x)<0,那么函数y=f(x)在这个区间内单调递减.
思考3 (1)如果一个函数具有相同单调性的单调区间不止一个,那么如何表示这些区间?试写出思考2中(4)的单调区间.
(2)函数的单调区间与其定义域满足什么关系?
答 (1)不能用“∪”连接,只能用“,”或“和”字隔开.思考2中(4)的单调递减区间为(-∞,0),(0,+∞).
(2)函数的单调性是对函数定义域内的某个子区间而言的,故单调区间是定义域的子集.
例1 已知导函数f′(x)的下列信息:
当1
0;
当x>4,或x<1时,f′(x)<0;
当x=4,或x=1时,f′(x)=0.
试画出函数f(x)图像的大致形状.
解 当10,可知f(x)在此区间内单调递增;
当x>4,或x<1时,f′(x)<0,可知f(x)在这两个区间内单调递减;
当x=4,或x=1时,f′(x)=0,这两点比较特殊,我们称它们为“临界点”.
综上,函数f(x)图像的大致形状如图所示.
反思与感悟 本题具有一定的开放性,图像不唯一,只要能抓住问题的本质,即在相应区间上的单调性符合题意就可以了.
跟踪训练1 函数y=f(x)的图像如图所示,试画出导函数f′(x)图像的大致形状.
解 f′(x)图像的大致形状如图:
注:图像形状不唯一.
探究点二 求函数的单调区间
例2 求下列函数的单调区间:
(1)f(x)=2x3+3x2-36x+1;
(2)f(x)=sin x-x(00得x<-3,或x>2,
由f′(x)<0解得-30,即2·>0,
解得-.
又∵x>0,∴x>.
令f′(x)<0,即2·<0,
解得x<-或00,∴00时,函数的单调递增区间是[-,].
令f′(x)≤0时,得3t-3x2≤0,即t≤x2,
当t≤0时,f′(x)≤0恒成立,
函数的单调递减区间是(-∞,+∞);
当t>0时,函数的单调递减区间是(-∞,-],[,+∞).
综上所述,当t≤0时,函数的单调减区间是(-∞,+∞),无单调增区间;
当t>0时,函数的单调增区间是[-,],单调减区间是(-∞,-],[,+∞).
反思与感悟 求函数的单调区间的具体步骤
(1)先确定f(x)的定义域;(2)再求导数f′(x);(3)后解定义域内满足f′(x)>0的区间为增区间,定义域内满足f′(x)<0的区间为减区间.
跟踪训练2 求下列函数的单调区间:
(1)f(x)=x2-ln x;(2)f(x)=x3-x2-x.
解 (1)函数f(x)的定义域为(0,+∞).
f′(x)=2x-=.
由f′(x)>0得-,
又∵x>0,∴x>,
∴函数f(x)的单调递增区间为;
由f′(x)<0得x<-或00,∴00得x<-或x>1;
由f′(x)<0得-0,∴函数在(0,6)上单调递增.
2.f′(x)是函数y=f(x)的导函数,若y=f′(x)的图像如图所示,则函数y=f(x)的图像可能是( )
答案 D
解析 由导函数的图像可知,当x<0时,f′(x)>0,即函数f(x)为增函数;当02时,f′(x)>0,即函数f(x)为增函数.观察选项易知D正确.
3.函数f(x)=ln(x2-x-2)的单调递减区间为________.
答案 (-∞,-1)
解析 f′(x)=,令f′(x)<0得x<-1或0,得x>2;
令y′<0,得x<2,
所以y=x2-4x+a的单调递增区间为(2,+∞),
单调递减区间为(-∞,2).
(2)y′=3x2-1,令y′>0,得x>或x<-;
令y′<0,得-0和f′(x)<0;
(4)根据(3)的结果确定函数f(x)的单调区间.
一、基础过关
1.命题甲:对任意x∈(a,b),有f′(x)>0;命题乙:f(x)在(a,b)内是单调递增的.则甲是乙的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
答案 A
解析 f(x)=x3在(-1,1)内是单调递增的,但f′(x)=3x2≥0(-10,∴00).
故函数在(1,+∞)上为单调减函数,
在(0,1)上为单调增函数.故选B.
5.函数y=f(x)在其定义域内可导,其图像如图所示,记y=f(x)的导函数为y=f′(x),则不等式f′(x)≤0的解集为__________________.
答案 ∪[2,3)
6.若三次函数f(x)=ax3+x在区间(-∞,+∞)内是增函数,则a的取值范围是________.
答案 (0,+∞)
解析 f′(x)=3ax2+1,∵f(x)在R上为增函数,
∴3ax2+1≥0在R上恒成立.又a≠0,∴a>0.
7.已知函数y=f(x)的导函数f′(x)的图像如图所示,试画出函数y=f(x)的大致图像.
解 由y=f′(x)的图像可以得到以下信息:x<-2或x>2时,
f′(x)<0,-20,f′(-2)=0,f′(2)=0.
故原函数y=f(x)的图像大致如图:
二、能力提升
8.已知函数y=xf′(x)的图像如图所示(其中f′(x)是函数f(x)的导函数),下面四个图像中y=f(x)的图像大致是( )
答案 C
解析 当x<-1时,xf′(x)<0,∴f′(x)>0,
∴当x<-1时,函数y=f(x)单调递增;
当-10,∴f′(x)<0,
∴当-11时,xf′(x)>0,∴f′(x)>0,
∴当x>1时,函数y=f(x)单调递增.
9.设f(x),g(x)在[a,b]上可导,且f′(x)>g′(x),则当ag(x)
B.f(x)g(x)+f(a)
D.f(x)+g(b)>g(x)+f(b)
答案 C
解析 ∵f′(x)-g′(x)>0,∴(f(x)-g(x))′>0,
∴f(x)-g(x)在[a,b]上是单调增函数,
∴当af(a)-g(a),
∴f(x)+g(a)>g(x)+f(a).
10.若函数f(x)=x2+ax+在(,+∞)是增函数,则a的取值范围是 ( )
A.[-1,0] B.[-1,+∞)
C.[0,3] D.[3,+∞)
答案 D
解析 由题意知f′(x)≥0对任意的x∈恒成立,
又f′(x)=2x+a-,
所以2x+a-≥0对任意的x∈恒成立,
分离参数得a≥-2x,
若满足题意,需a≥max.
令h(x)=-2x,x∈.
因为h′(x)=--2,
所以当x∈时,h′(x)<0,
即h(x)在上单调递减,
所以h(x)<h=3,故a≥3.
11.求下列函数的单调区间:
(1)y=x-ln x; (2)y=ln(2x+3)+x2.
解 (1)函数的定义域为(0,+∞),y′=1-,
由y′>0,得x>1;由y′<0,得00,即--时,
函数y=ln(2x+3)+x2单调递增;
当y′<0,即-10,得x<1-或x>1+;
令f′(x)<0,得1-0时,ln(x+1)>x-x2.
证明 设f(x)=ln(x+1)-(x-x2)=ln(x+1)-x+x2,函数的定义域是(-1,+∞).
则f′(x)=-1+x=.
当x∈(-1,+∞)时,f′(x)>0,
∴f(x)在(-1,+∞)上是增函数.
∴当x>0时,f(x)>f(0)=0,
即当x>0时,ln(x+1)>x-x2.