- 2021-06-16 发布 |
- 37.5 KB |
- 18页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
陕西省安康中学2020届高三下学期仿真模拟数学(文)试题 Word版含解析
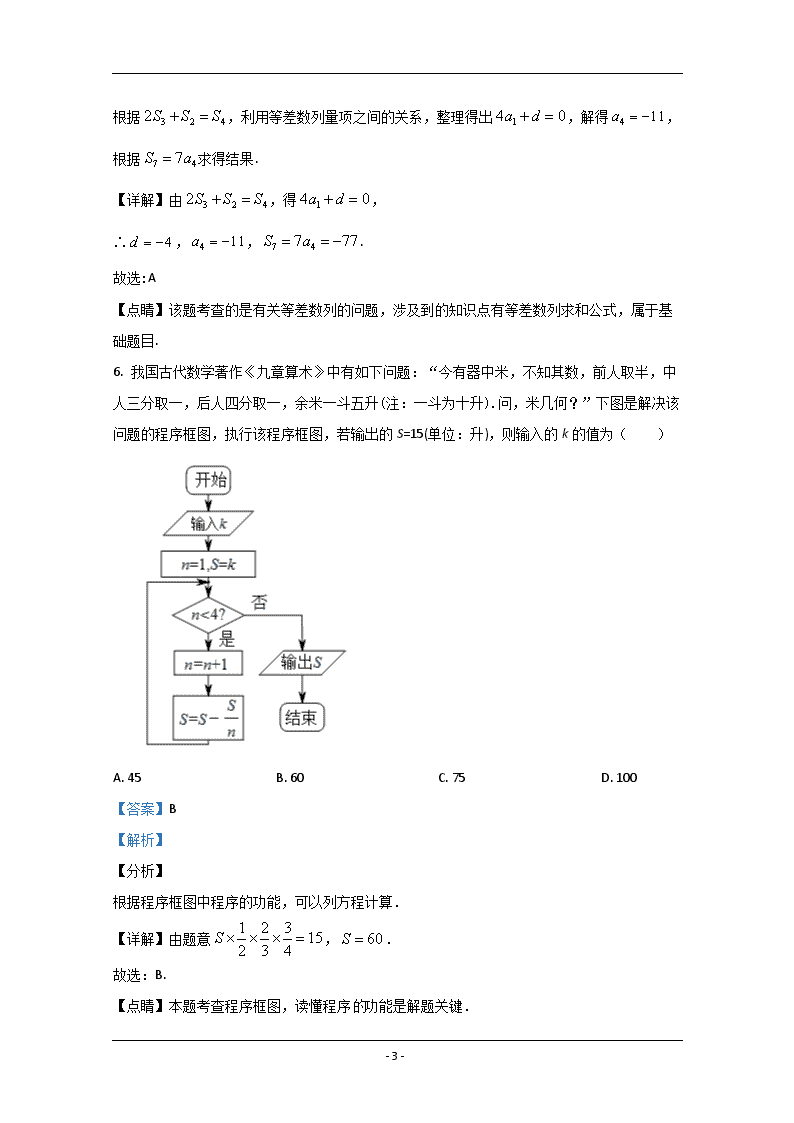
2020年高三仿真模拟考试 一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1. 已知全集,集合,( ) A. B. C. D. 【答案】A 【解析】 【分析】 解一元二次不等式求得全集,由此求得. 【详解】由,解得,所以,所以. 故选:A 【点睛】本小题主要考查一元二次不等式的解法,考查集合补集的概念和运算,属于基础题. 2. 已知复数,则在复平面内对应的点位于( ) A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限 【答案】B 【解析】 【分析】 利用复数除法运算化简,由此求得,进而求得对应点所在象限. 【详解】依题意,所以,对应点为,在第二象限. 故选:B 【点睛】本小题主要考查复数除法运算,考查共轭复数,考查复数对应点所在象限,属于基础题. 3. 已知向量,,,则( ). A. B. 2 C. D. 1 - 18 - 【答案】D 【解析】 分析】 直接利用向量的坐标运算以及向量的数量积求解即可. 【详解】,. 故选:D. 【点睛】本题考查向量的数量积的应用,向量的坐标运算,是基本知识的考查,属于基础题. 4. 造纸术、印刷术、指南针、火药被称为中国古代四大发明,此说法最早由英国汉学家艾约瑟提出并为后来许多中国的历史学家所继承,普遍认为这四种发明对中国古代的政治、经济、文化的发展产生了巨大的推动作用.某小学三年级共有学生400名,随机抽查100名学生并提问中国古代四大发明,能说出两种及其以上发明的有73人,据此估计该校三年级的400名学生中,对四大发明只能说出一种或一种也说不出的有( ). A. 69人 B. 84人 C. 108人 D. 115人 【答案】C 【解析】 【分析】 先求得名学生中,只能说出一种或一种也说不出的人数,由此列出比例式,可求得名学生中,对四大发明只能说出一种或一种也说不出的人数. 【详解】在这100名学生中,只能说出一种或一种也说不出的有人, 设该校三年级的400名学生中,对四大发明只能说出一种或一种也说不出的有人, 则,解得人. 故选:C. 【点睛】本小题主要考查利用样本估计总体,属于基础题. 5. 记为等差数列的前项和,,,则( ) A. -77 B. -70 C. -49 D. -42 【答案】A 【解析】 【分析】 - 18 - 根据,利用等差数列量项之间的关系,整理得出,解得,根据求得结果. 【详解】由,得, ∴,,. 故选:A 【点睛】该题考查的是有关等差数列的问题,涉及到的知识点有等差数列求和公式,属于基础题目. 6. 我国古代数学著作《九章算术》中有如下问题:“今有器中米,不知其数,前人取半,中人三分取一,后人四分取一,余米一斗五升(注:一斗为十升).问,米几何?”下图是解决该问题的程序框图,执行该程序框图,若输出的S=15(单位:升),则输入的k的值为( ) A. 45 B. 60 C. 75 D. 100 【答案】B 【解析】 【分析】 根据程序框图中程序的功能,可以列方程计算. 【详解】由题意,. 故选:B. 【点睛】本题考查程序框图,读懂程序功能是解题关键. - 18 - 7. 已知双曲线的焦距是虚轴长的2倍,则双曲线的渐近线方程为( ) A. B. C. D. 【答案】A 【解析】 【分析】 根据双曲线的焦距是虚轴长的2倍,可得出,结合,得出,即可求出双曲线的渐近线方程. 【详解】解:由双曲线可知,焦点在轴上, 则双曲线的渐近线方程为:, 由于焦距是虚轴长的2倍,可得:, ∴, 即:,, 所以双曲线的渐近线方程为:. 故选:A. 【点睛】本题考查双曲线的简单几何性质,以及双曲线的渐近线方程. 8. 已知直线是曲线的切线,则( ) A. 或1 B. 或2 C. 或 D. 或1 【答案】D 【解析】 【分析】 求得直线的斜率,利用曲线 - 18 - 的导数,求得切点坐标,代入直线方程,求得的值. 【详解】直线斜率为, 对于,令,解得,故切点为,代入直线方程得,解得或1. 故选:D 【点睛】本小题主要考查根据切线方程求参数,属于基础题. 9. 正三棱柱中,,是的中点,则异面直线与所成的角为( ) A. B. C. D. 【答案】C 【解析】 【分析】 取中点,连接,,根据正棱柱的结构性质,得出//,则即为异面直线与所成角,求出,即可得出结果. 【详解】解:如图,取中点,连接,, 由于正三棱柱,则底面, 而底面,所以, 由正三棱柱的性质可知,为等边三角形, 所以,且, - 18 - 所以平面, 而平面,则, 则//,, ∴即为异面直线与所成角, 设,则,,, 则, ∴. 故选:C. 【点睛】本题考查通过几何法求异面直线的夹角,考查计算能力. 10. 地铁某换乘站设有编号为,,,,五个安全出口.若同时开放其中的两个安全出口,疏散1000名乘客所需的时间如下: 安全出口编号 , , , , , 疏散乘客时间() 120 220 160 140 200 则疏散乘客最快的—个安全出口的编号是( ) A. B. C. D. 【答案】C 【解析】 【分析】 比较开放、和开放、两个安全出口,得出疏散乘客比快;同理可得出疏散乘客最快的一个安全出口的编号是. 【详解】同时开放、两个安全出口,疏散1000名乘客所需的时间为,同时开放、两个安全出口,疏散1000名乘客所需的时间为,所以疏散乘客比快;同理可得 - 18 - 疏散乘客比快,疏散乘客比快,疏散乘客比快,疏散乘客比快,所以疏散乘客最快的一个安全出口的编号是. 故选:C 【点睛】本题主要考查了推理与证明的知识,属于基础题. 11. 已知是定义在上的偶函数,且在单调递增,设,,,则( ). A. B. C. D. 【答案】B 【解析】 【分析】 根据函数的单调性以及奇偶性求解即可. 【详解】∵是偶函数且在上单调递增 ∴ ∵,∴ 故选:B 【点睛】本题主要考查了根据函数的单调性以及奇偶性比较大小,属于中档题. 12. 过抛物线:的焦点的直线交于,两点,设,在轴上的投影分别为,,若,则直线的斜率为( ) A. B. C. D. 【答案】C 【解析】 【分析】 由抛物线定义知,结合题设可得,可设直线:,根据它与抛物线的交点,,联立方程并利用根与系数关系有,而,即可求直线的斜率 - 18 - 【详解】由已知及抛物线的定义,可得 ∴.设直线:,若, 则,有 由,得 故选:C 【点睛】本题考查求过抛物线焦点的直线斜率,由抛物线的定义、结合题设条件求得焦点弦的长度,联立直线与抛物线方程,利用根与系数关系、焦点弦长的坐标表示即可求直线斜率 二、填空题:本题共4小题,每小题5分,共20分. 13. 已知圆柱的两个底面的圆周在同一个球的球面上,圆柱的高和球半径均为2,则该圆柱的体积为______. 【答案】 【解析】 【分析】 建立勾股定理即可计算出圆柱底面半径,即可求得体积. 【详解】设圆柱底面半径为,由已知有,∴, 体积. 故答案为:. 【点睛】本题考查由圆柱的外接球的性质求圆柱底面半径,属于基础题. 14. 若,满足约束条件,则的最大值为______. 【答案】3 【解析】 【分析】 如图,先画出约束条件所表示的可行域,由目标函数得,作直线向下平移过点A时,取最大值,将点A的坐标代入即可得答案. - 18 - 【详解】解:,满足约束条件所表示的可行域如图所示, 由目标函数,得,要取得最大值,只要直线的截距最小即可,所以将直线向下平移过点A时,取最大值, 由,得,即点A的坐标为, 所以的最大值为 故答案为:3 【点睛】此题考查简单的线性规划的应用,属于基础题. 15. 已知等比数列的各项均为正数,,,则数列的前10项的和为______. 【答案】 【解析】 【分析】 由题设知等比数列的公比,即可得其通项公式,由数列知,利用裂项求和的方法即可求前10项的和 【详解】令等比数列的公比为,则,且各项均为正数 - 18 - ∴, ∴ ∴前10项的和为 故答案为: 【点睛】本题考查利用裂项法求前n项和,根据等比数列的已知项求通项公式,进而求新数列的通项公式,再应用裂项法求前n项和 16. 已知函数,若方程的解为,则______. 【答案】 【解析】 【分析】 由已知求出的范围,根据方程的解的对称性可得答案. 【详解】∵,∴, ∵方程的解为,∴, 解得. 故答案为:. 【点睛】本题考查了三角函数的对称性,整体带入比较方便. 三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答. (一)必考题:共60分. 17. 已知,,分别为内角,,的对边,,. - 18 - (1)求; (2)若,的面积为,求,的值. 【答案】(1);(2). 【解析】 【分析】 (1)利用辅助角公式可得,从而得到的关系,结合可得,从而可求得的值. (2)利用余弦定理和面积公式可得,从而可求的值. 【详解】(1)因为, 故即, 所以或,. 因为,,故或, 因为,所以,故不成立, 所以即. (2)因为,由余弦定理可得, 整理得到. 因为的面积为,所以即. 由可得. 【点睛】 - 18 - 本题考查辅助角公式以及正弦定理、余弦定理在解三角形中的应用,一般地,三角形中共有七个几何量(三边三角以及外接圆的半径),我们可利用已知条件构建所求未知量的方程组,本题属于中档题. 18. 如图,直三棱柱中,是的中点,是的中点. (1)证明:平面; (2)若,,求四棱锥的体积. 【答案】(1)证明见解析;(2). 【解析】 【分析】 (1)取的中点,连接,,根据四边形为平行四边形,可得,根据直线与平面平行的判定定理可证平面; (2)现根据长度可得底面时等腰直角三角形,其斜边上的高为四棱锥的高,再根据棱锥的体积公式可得结果. 【详解】(1)取中点,连接,,如图: 则,,∴, ∴四边形为平行四边形,∴, - 18 - ∵平面,平面,∴平面. (2)因为,,所以,所以, 所以斜边上的高为,即四棱锥的高为, ∴. 【点睛】本题考查了直线与平面平行的判定定理,考查了棱锥的体积公式,属于基础题. 19. 科技改变生活,方便生活.共享单车的使用就是云服务的一种实践,它是指人民政府合作,为居民出行提供单车共享服务,它符合低碳出生理念,为解决城市出行的“最后一公里”提供了有力支撑,是共享经济的一种新形态.某校学生社团为研究当地使用共享单车人群的年龄状况,随机抽取了当地100名使用共享单车的群众作出调查,所得频率分布直方图如图所示. (1)估计当地共享单车使用者年龄的中位数; (2)若按照分层抽样从年龄在,的人群中抽取5人,再从这5人中随机抽取2人调查单车使用体验情况,求抽取的2人中年龄都在的概率. 【答案】(1)中位数为41;(2). 【解析】 【分析】 (1)由频率和为1可构造方程求得a;根据频率分布直方图估计中位数的方法可计算求得中位数; (2)根据分层抽样方法的规矩,求得年龄在,内的人数,应用列举法得出其对应的基本事件,找出满足条件的基本事件数,应用古典概型概率公式求得结果. - 18 - 【详解】(1)由,解得, 该共享单车使用者年龄的中位数为, 则,解得, ∴估计使用者年龄的中位数为41. (2)抽取的5人中有人年龄在内,设为,, 3人年龄在内,设为,,. 5人中随机抽取2人有,,,,,,,,,, 共10种情况,其中2人年龄都在的有3种情况, 故概率. 【点睛】该题考查的是有关概率与统计的问题,涉及到的知识有利用频率分布直方图求中位数,分层抽样,古典概型,属于简单题目. 20. 已知椭圆:过点,且离心率为. (1)求椭圆的方程; (2)过椭圆的上顶点作两条互相垂直的直线分别交于,两点,若的平分线方程为,求直线与的斜率之和. 【答案】(1);(2). 【解析】 【分析】 (1)根据椭圆:过点,且离心率为,由求解. - 18 - (2)易得,直线过定点,,再根据且直线是角平分线,得到到,的距离为,然后设:,利用点到直线的距离,由求解. 【详解】(1)因为椭圆:过点,且离心率为, 所以, 解得,, 所以椭圆的方程为. (2),在直线上取点,则,到,的距离为, 设:,则,或, ∴直线与的斜率之和为. 【点睛】本题主要考查椭圆方程的求法以及角平分线和点到直线距离的应用,还考查了转化求解问题的能力,属于中档题. 21. 已知函数. (1)若,求的最小值﹔ (2)若有且仅有一个零点,求的取值范围. 【答案】(1);(2)或. - 18 - 【解析】 【分析】 (1)求出函数的单调性,即得在处取得最小值; (2)当时,仅有一个零点,满足题意;当时,令得,由零点存在定理知存在唯一的,使得成立,即, 得到在处取得最小值,即得,综合即得解. 【详解】(1)当时,, 当时,,单调递减,当时,,单调递增, ∴在处取得最小值. (2), ∵,∴1是的一个零点, 当时,为上的增函数,∴仅有一个零点,满足题意, 当时,令得, ∵在上是增函数,,, 由零点存在定理知存在唯一的,使得成立,即, 当时,,为减函数,当时,,为增函数, ∴在处取得最小值, ∵只有一个零点,∴, 又,∴,∴, 综上可得或. 【点睛】本题主要考查利用导数研究函数的最值,考查利用导数研究函数的零点问题,意在考查学生对这些知识的理解掌握水平. - 18 - (二)选考题:共10分.请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题计分. 22. 在直角坐标系中,曲线的参数方程为(为参数),以为极点,轴正半轴为极轴,建立极坐标系,曲线的极坐标方程为. (1)写出的普通方程与的直角坐标方程﹔ (2)设点在上,、分别是与、轴的交点,求面积的最小值. 【答案】(1)的普通方程为,的直角坐标方程为;(2). 【解析】 【分析】 (1)利用消去参数,求得的普通方程,结合两角差的余弦公式化简,求得的直角坐标方程. (2)根据、分别是与、轴的交点,得到、的坐标以及,根据点到直线距离公式,结合辅助角公式以及三角形的面积公式,求得面积的最小值. 【详解】(1)由,求得的普通方程为, 由化简得,所以的直角坐标方程为; (2)由(1)知,,∴, 设点,则点到的距离 - 18 - ∴. 【点睛】本小题主要考查参数方程化为普通方程,考查极坐标方程化为直角坐标方程,考查利用参数方程求椭圆上的点到直线的距离的最小值以及三角形面积的最值,属于中档题. 23. 已知函数. (1)当时,求的解集; (2)当时,,求的取值范围. 【答案】(1);(2). 【解析】 【分析】 (1)根据绝对值不等式的解法求解即可. (2)将问题转化为当时,恒成立,再求在上的最值即可. 【详解】(1)当时,可化为, 即,, ∴或,解得或, ∴的解集为. (2)可化为,即. ∵在上的最大值为3,最小值为0, ∴,解得. 故的取值范围为:. 【点睛】本题考查绝对值不等式的解法,不等式恒成立问题,是中档题. - 18 -查看更多