- 2021-06-16 发布 |
- 37.5 KB |
- 10页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
【数学】安徽省合肥市2020届高三第三次教学质量检测(文)
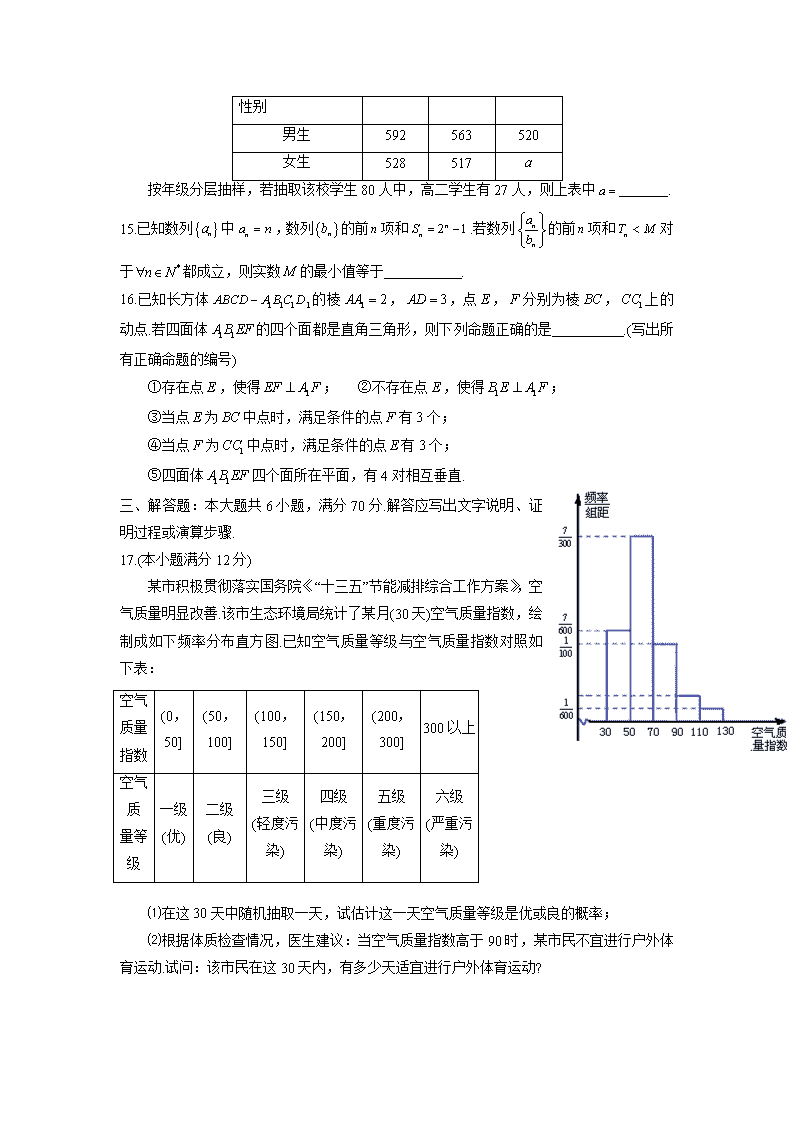
安徽省合肥市2020届高三第三次教学质量检测(文) (考试时间:120分钟 满分:150分) 第Ⅰ卷 (60分) 一、选择题:本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.若集合,集合,则 A. B. C. D. 2.已知是虚数单位,则复数在复平面上所对应的点位于 A.第一象限 B.第二象限 C.第三象限 D.第四象限 3.在新冠肺炎疫情联防联控期间,某居委会从辖区内A,B,C三个小区志愿者中各选取1人,随机安排到这三个小区,协助小区保安做好封闭管理和防控宣传工作.若每个小区安排1人,则每位志愿者不安排在自己居住小区的概率为 A. B. C. D. 4.若,则是成立的 A.充分不必要条件 B.必要不充分条件 C.充分必要条件 D.既不充分也不必要条件 5.已知函数(),则不等式的解集是 A. B. C. D. 6.已知向量,满足,其中是单位向量,则在方向上的投影是 A.1 B. C. D. 7.公元前1650年的埃及莱因德纸草书上载有如下问题:“十人分十斗玉米,从第二人开始,各人所得依次比前人少八分之一,问每人各得玉米多少斗?”在上述问题中,第一人分得玉米 A.斗 B.斗 C.斗 D.斗 8.在中,若,则 A.的最大值为 B.的最大值为 C.的最小值为 D.的最小值为 9.某校高一年级研究性学习小组利用激光多普勒测速仪实地测量复兴号高铁在某时刻的速度,其工作原理是:激光器发出的光平均分成两束射出,在被测物体表面汇聚,探测器接收反射光.当被测物体横向速度为零时,反射光与探测光频率相同.当横向速度不为零时,反射光相对探测光会发生频移,其中为测速仪测得被测物体的横向速度,为激光波长,为两束探测光线夹角的一半,如图.若激光测速仪安装在距离高铁1处,发出的激光波长为1550(),测得某时刻频移为(1/h),则该时刻高铁的速度约等于 A.320km/h B.330km/h C.340km/h D.350km/h 10.经过抛物线的焦点的直线交抛物线于,两点,则的最小值为 A. B.5 C.9 D.10 11.点是正方体的侧面内的一个动点,若与的面积之比等于2,则点的轨迹是 A.圆的一部分 B.椭圆的一部分 C.双曲线的一部分 D.抛物线的一部分 12.若关于的不等式在区间(为自然对数的底数)上有实数解,则实数的最大值是 A. B. C. D. 第II卷 (90分) 本卷包括必考题和选考题两部分.第13题—第21题为必考题,每个试题考生都必须作答.第22题、第23题为选考题,考生根据要求作答. 二、填空题:本大题共4小题,每小题5分,满分20分.把答案填在答题卡上的相应位置. 13.设函数(其中为自然对数的底数),则的值等于 . 14.某高中各年级男、女生人数如下表: 人数 年级 高一 高二 高三 性别 男生 592 563 520 女生 528 517 按年级分层抽样,若抽取该校学生80人中,高二学生有27人,则上表中 . 15.已知数列中,数列的前项和.若数列的前项和对于都成立,则实数的最小值等于 . 16.已知长方体的棱,,点,分别为棱,上的动点.若四面体的四个面都是直角三角形,则下列命题正确的是 .(写出所有正确命题的编号) ①存在点,使得; ②不存在点,使得; ③当点为中点时,满足条件的点有3个; ④当点为中点时,满足条件的点有3个; ⑤四面体四个面所在平面,有4对相互垂直. 三、解答题:本大题共6小题,满分70分.解答应写出文字说明、证明过程或演算步骤. 17.(本小题满分12分) 某市积极贯彻落实国务院《“十三五”节能减排综合工作方案》,空气质量明显改善.该市生态环境局统计了某月(30天)空气质量指数,绘制成如下频率分布直方图.已知空气质量等级与空气质量指数对照如下表: 空气质量指数 (0,50] (50,100] (100,150] (150,200] (200,300] 300以上 空气质 量等级 一级 (优) 二级 (良) 三级 (轻度污染) 四级 (中度污染) 五级 (重度污染) 六级 (严重污染) ⑴在这30天中随机抽取一天,试估计这一天空气质量等级是优或良的概率; ⑵根据体质检查情况,医生建议:当空气质量指数高于90时,某市民不宜进行户外体育运动.试问:该市民在这30天内,有多少天适宜进行户外体育运动? 18.(本小题满分12分) 如图,边长为2的等边所在平面与菱形所在平面互相垂直,且,,. ⑴求证:∥平面; ⑵求多面体的体积. 19.(本小题满分12分) 已知函数()的部分图象如图所示. ⑴求函数的解析式; ⑵将函数的图象向左平移个单位,再将图象上各点的横坐标伸长到原来的2倍(纵坐标不变)得到函数的图象,求函数在区间上的值域. 20.(本小题满分12分) 在平面直角坐标系中,已知点是椭圆:上的动点,不经过点的直线交椭圆于,两点. ⑴若直线经过坐标原点,证明:直线与直线的斜率之积为定值; ⑵若,证明:三边的中点在同一个椭圆上,并求出这个椭圆的方程. 21.(本小题满分12分) 已知函数(为自然对数的底数),其中. ⑴试讨论函数的单调性; ⑵当时,记函数,的图象分别为曲线,.在上取点()作轴的垂线交于,再过点作轴的垂线交于()(),且. ①用表示; ②设数列和的前项和分别为,求证: 请考生在第(22)、(23)题中任选一题作答.注意:只能做所选定的题目,如果多做,则按所做的第一个题目计分,作答时,请用2B铅笔在答题卡上,将所选题号对应的方框涂黑. 22.(本小题满分10分)选修4-4:坐标系与参数方程 在平面直角坐标系中,直线的参数方程为(为参数,).以坐标原点为极点,以轴的非负半轴为极轴建立极坐标系.曲线的极坐标方程为,直线与曲线交于,两点. ⑴求曲线的直角坐标方程和直线的极坐标方程; ⑵过原点且与直线垂直的直线,交曲线于,两点,求四边形面积的最大值. 23.(本小题满分10分)选修4-5:不等式选讲 已知函数的最小值为. ⑴求的值; ⑵若,证明:. 参考答案 一、选择题:本大题共12小题,每小题5分,共60分. 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 B C B B D C B A D C A D 二、填空题:本大题共4小题,每小题5分,共20分. 13. 14.480 15.4 16.①②④ 三、 解答题:本大题共6小题,满分70分. 17.(本小题满分12分) 解:(1)由题中图表可知,在这30天中,空气质量指数在区间内的天数为 天, 空气质量等级为优或良,即空气质量指数不超过100, ∴在这30天中随机抽取一天,其空气质量等级是优或良的概率为. ………………………6分 (2)由题中图表可知,在这30天中,空气质量指数不高于90有 (天), ∴某市民在这个月内,有27天适宜进行户外体育运动. ………………………12分 18.(本小题满分12分) 解:(1)∵四边形是菱形,∴∥. 又∵平面,平面,∴∥平面. 同理得,∥平面. ∵,平面,且, ∴平面∥平面. 又∵平面, ∴∥平面. …………5分 (2)∵∥,∥,∴. ∵,, ∴. 在菱形中,∵, ∴,. ∵平面⊥平面,取的中点为,连接, ∴⊥平面,⊥平面. 由(1)知,平面∥平面, ∴点到平面的距离为. 又∵点到平面的距离为,连接, 则. ………………………………12分 19.(本小题满分12分) 解:(1)由已知得(),解得, ∴. ……………………………6分 (2)由题意得,. ∵,∴, ∴, ∴的值域为. ……………………………12分 20.(本小题满分12分) 解:设点,,. (1)∵直线经过坐标原点,∴. ∵,∴. 同理得,. ∴, ∴直线与直线的斜率之积为定值. ……………………………6分 (2)设线段的中点为,则 ∵,∴,则. 将代入得,, ∴线段的中点的轨迹方程为. 同理,线段和线段中点的轨迹方程也为. ∴三边的中点在同一个椭圆上. ……………………………12分 21.(本小题满分12分) 解:(1). 当时,恒成立,在上单调递增. 当时,由得,,∴. ∴在和上单调递增, 在上单调递减. …………………………………5分 (2)①由(1)知,当时,,即当时,曲线恒在上方. 按题意有,,即,∴. ②由①知. 注意到, ∴, ∴, 两边同取自然对数得,, 即. …………………………………………12分 22.(本小题满分10分) (1)曲线的直角坐标方程为, 直线的极坐标方程为(). ………………………………5分 (2)设点,的极坐标分别为,. 由得,, ∴,, ∴. 同理得,. ∵, 当且仅当,即时,等号成立, ∴四边形面积的最大值为7. ………………………………10分 23.(本小题满分10分) (1), 根据函数图象得,的最小值为-2, ∴. ………………………………5分 (2)由(1)知,, ∴, ∴, 当且仅当,,即,,时等号成立, ∴. ………………………………10分查看更多