- 2021-06-16 发布 |
- 37.5 KB |
- 25页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2019届二轮复习不等式选讲学案(全国通用)(理)
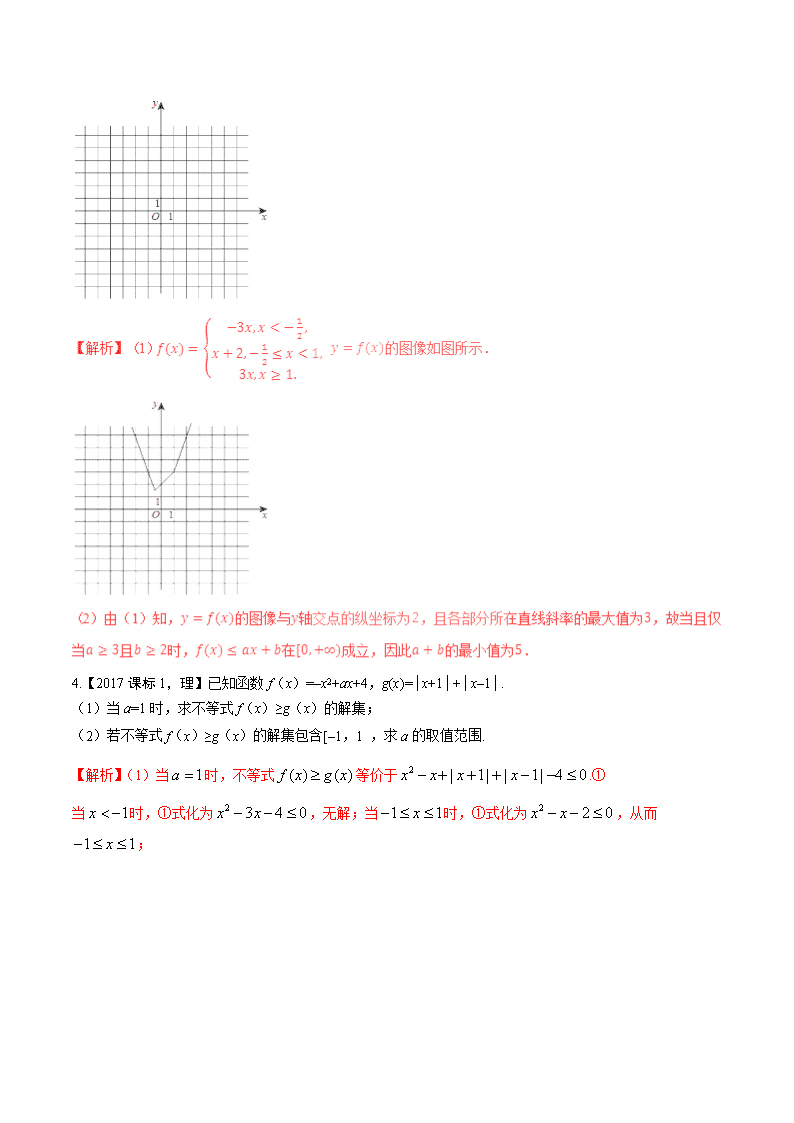
【三年高考精选】 1. 【2018 年理新课标 I 卷】已知 . (Ⅰ)当 时,求不等式 的解集; (Ⅱ)若 时不等式 成立,求 的取值范围. 2. 【2018 年理数全国卷 II】设函数 . (1)当 时,求不等式 的解集; (2)若 ,求 的取值范围. 【解析】(1)当 时, 可得 的解集为 . (2) 等价于 .而 ,且当 时等号成立.故 等 价于 .由 可得 或 ,所以 的取值范围是 . 3. 【2018 年全国卷Ⅲ理】设函数 . (1)画出 的图像; (2)当 , ,求 的最小值. 4.【2017 课标 1,理】已知函数 f(x)=–x2+ax+4,g(x)=│x+1│+│x–1│. (1)当 a=1 时,求不等式 f(x)≥g(x)的解集; (2)若不等式 f(x)≥g(x)的解集包含[–1,1 ,求 a 的取值范围. 【解析】(1)当 1a 时,不等式 ( ) ( )f x g x 等价于 2 | 1| | 1| 4 0x x x x .① 当 1x 时,①式化为 2 3 4 0x x ,无解;当 1 1x 时,①式化为 2 2 0x x ,从而 1 1x ; 5.【2017 课标 II,理】已知 3 30, 0, 2a b a b 。证明: (1) 5 5( )( ) 4a b a b ;(2) 2a b 。 【解析】 (1) 2 25 5 6 5 5 6 3 3 3 3 4 4 2 22 4 4a b a b a ab a b b a b a b ab a b ab a b (2)因为 2 3 3 3 2 2 3 3 33 3 2 3 2 2 ,4 4 a b a ba b a a b ab b ab a b a b 所以 3 8a b ,因此 2a b 。 6.【2017 课标 3,理】已知函数 f(x)=│x+1│–│x–2│. (1)求不等式 f(x)≥1 的解集; (2)若不等式 2f x x x m 的解集非空,求 m 的取值范围. 【解析】(1) 3 < 1 2 1 1 2 3 >2 , x f x x , x , x ,当 < 1x 时, 1f x 无解;当 1 2x 时,由 1f x 得, 2 1 1x ,解得1 2x ,当 >2x 时,由 1f x 解得 >2x .所以 1f x 的解集为 1x x . (2)由 2f x x x m 得 21 2m x x x x ,而 x x x x x x x x x 2 2 2 3 5 51 2 +1+ 2 =- - +2 4 4 ,且当 3 2x 时, 2 51 2 = 4x x x x .故 m 的取值范围为 5- ,4 . 7.【2016 高考新课标 1 理数】已知函数 1 2 3f x x x . (I)在答题卡第(24)题图中画出 y f x 的图像; (II)求不等式 1f x 的解集. 8.【2016 高考新课标 2 理数】已知函数 1 1( ) | | | |2 2f x x x , M 为不等式 ( ) 2f x 的解集. (Ⅰ)求 M ; (Ⅱ)证明:当 ,a b M 时,| | |1 |a b ab . 【解析】(I) 12 , ,2 1 1( ) 1, ,2 2 12 , .2 x x f x x x x 当 1 2x 时,由 ( ) 2f x 得 2 2,x 解得 1x ;当 1 1 2 2x 时, ( ) 2f x ;当 1 2x 时,由 ( ) 2f x 得 2 2,x 解得 1x .所以 ( ) 2f x 的解集 { | 1 1}M x x . (II)由(I)知,当 ,a b M 时, 1 1, 1 1a b ,从而 2 2 2 2 2 2 2 2( ) (1 ) 1 ( 1)(1 ) 0a b ab a b a b a b ,因此| | |1 |.a b ab 9.【2016 高考新课标 3 理数】已知函数 ( ) | 2 |f x x a a . (I)当 2a 时,求不等式 ( ) 6f x 的解集; (II)设函数 ( ) | 2 1|g x x .当 xR 时, ( ) ( ) 3f x g x ,求 a 的取值范围. 【三年高考刨析】 试题 考查考点 数素养 解题关键 2018 全国理 1 解绝对值不等式 数运算 数抽象 准确掌握解绝对值不等式的解题方法,并能灵 活应用 2018 全国理 2 解绝对值不等式 数运算 数抽象 准确掌握解绝对值不等式的解题方法,并能灵 活应用 2018 全国理 3 解绝对值不等式 数运算 数抽象 准确掌握解绝对值不等式的解题方法,并能灵 活应用 2017 全国理 1 解绝对值不等式 数运算 数抽象 准确掌握解绝对值不等式的解题方法,并能灵 活应用 2017 全国理 2 不等式证明 数运算 数抽象 准确掌握不等式证明的解题方法,并能灵活应 用 2017 全国理 3 解绝对值不等式 数运算 数抽象 准确掌握解绝对值不等式的解题方法,并能灵 活应用 2016 全国理 1 解绝对值不等式 数运算 数抽象 准确掌握解绝对值不等式的解题方法,并能灵 活应用 2016 全国理 2 解绝对值不等式,不等 式证明 数运算 数抽象 准确掌握解绝对值不等式与不等式证明的解 题方法,并能灵活应用 2016 全国理 3 解绝对值不等式 数运算 数抽象 准确掌握解绝对值不等式的解题方法,并能灵 活应用 命题 规律 总结 对不等式选讲的考查,主要考查绝对值不等式,柯西不等式,基本不等式等知识,主要 考查绝对值不等式的解法,绝对值不等式的最值,绝对值不等式的恒成立问题,利用柯 西不等式,基本不等式求最值,题目难度一般为中、低档,着重考查利用数形结合的能 力以及化归与转化思想. 【2019 年高考命题预测】 预测 2019 高考,绝对值不等式仍是考试的重点,也有可能出一个利用柯西不等式求最值.考查绝对值不等 式的基础知识,基本技能,基本方法,还考查了分析问题、解决问题的能力.预计绝对值不等式的性质,绝 对值不等式的解法及重要不等知识,解绝对值不等与利用柯西不等式证不等式.如果是解绝对值不等式含参 数的绝对值不等式可能性比较大,如果是证明题将是利用柯西不等式. …… 【2019 年一轮复习指引】 由前三年的高考命题形式可以看出,高考对这部分要求不是太高,会解绝对值不等式,会利用柯西不等式 求最值,而解绝对值不等式是高考的热点,备考中应严格控制训练题的难度.高考对这部分要求不是太高, 高考中有选择题和填空的形式,新课标等以选做题的形式考查.高考复习建议:在复习解绝对值不等式过程 中,注意培养、强化与提高等价转化、分类讨论、数形结合的数思想和方法,逐步提升数素养,提高分析 解决综合问题的能力. 能根椐各类不等式的特点,变形的特殊性,归纳出各类绝对值不等式的解法和思路以 及具体解法.利用函数知识解应用题是高考重点,应引起重视. . 【2019 年高考考点定位】 高考对不等式选讲的考查有含绝对值不等式的解法,有关不等式的证明,利用不等式的性质求最值. 考点一、绝对值不等式 典例 1【江西省 2018 届六校联考】设函数 (1)当 时,解不等式 ; (2)求证: . 【备考知识梳理】 1.绝对值三角不等式 (1)定理 1:如果 ,a b 是实数,则 a b a b a b ,对于 a b a b ,当且仅当 0ab 时,等号 成立. (2)定理 2:如果 , ,a b c 是实数,则 a c a b b c ,当且仅当 0a b b c 时,等号成立. 2.绝对值不等式的解法 (1)含绝对值的不等式 x a 与 x a 的解集: 不等式 0a 0a 0a x a ,a a x a , ,a a ,0 0, R (2) ax b c ( 0c )和 ax b c ( 0c )型不等式的解法: ① ax b c c ax b c ; ② ax b c ax b c 或 ax b c ; (3) x a x b c ( 0c )和 x a x b c ( 0c )型不等式的解法: ①利用绝对值不等式的几何意义求解,体现了数形结合的思想; ②利用“零点分段法”求解,体现了分类讨论的思想; ③通过构造函数,利用函数的图象求解,体现了函数与方程的思想. 3.易错点形如 x a x b c 的不等式解法在讨论时应注意分类讨论点处的处理及 c 的符号判断,若 0c 则不等式解集为 R . 【规律方法技巧】 1.解含有绝对值不等式时,去掉绝对值符号的方法主要有:公式法、分段讨论法、平方法、几何法等.这几 种方法应用时各有利弊,在解只含有一个绝对值的不等式时,用公式法较为简便;但是若不等式含有多个 绝对值时,则应采用分段讨论法;应用平方法时,要注意只有在不等式两边均为正的情况下才能运用.因 此,在去绝对值符号时,用何种方法需视具体情况而定. 2. 含绝对值不等式的常用解法 (1)基本性质法:对 0a , x a a x a , x a x a 或 x a . (2)平方法:两边平方去掉绝对值符号.这适应于两边都是正数的绝对值不等式. (3)零点分区间法(或叫定义法):含有两个或两个以上绝对值符号的不等式,可用零点分区间法脱去绝对值符 号,将其转化为与之等价的不含绝对值符号的不等式(组)求解. . 用零点分段法解绝对值不等式的步骤:①求零点; ②划区间,去掉绝对值符号; ③分别解去掉绝对值的不等式; ④取每个结果的并集,注意在分段时不要遗漏区间的端点值. (4)几何法:利用绝对值的几何意义,画出数轴,将绝对值转化为数轴上两点的距离求解. (5)数形结合法:在直角坐标系中作出不等式两边所对应的两个函数的图象,利用函数图象求解. 3.证明绝对值不等式主要有三种方法 (1)利用绝对值的定义去掉绝对值符号,转化为普通不等式再证明; (2)利用三角不等式 a b a b a b 进行证明; (3)转化为函数问题,数形结合进行证明. 4 对于求 y x a x b 或 y x a x b 型的最值问题利用绝对值三角不等式更方便.形如 y x a x b 的函数只有最小值,形如 y x a x b 的函数既有最大值又有最小值. 【考点针对训练】 1. 【内蒙古包头市 2018 届一模】已知函数 , . (1)当 时,求不等式 的解集; (2)若不等式 的解集包含 ,求 的取值范围. 2. 【湖北省 2018 届重点高中联考】已知函数 1f x x x a . (1)若 2a ,解关于 x 的不等式 0f x x ; (2)若 x R ,使 4f x ,求 a 的取值范围. 【解析】(1)当 2a 时,① 2, 1 2 0 3 2x f x x x x x x ② ③ 1, 1 2 0x f x x x x x x ,综上可知:当 2a 时,原不等式的解集为 3 1x x (2) 1 +f x x x a 表示 x 到 1 a 和 的距离之和, min 1f x a , 1 4, 3 5a a 【考点 2】不等式的证明 典例 2【安徽省芜湖市 2018 届一模】已知函数 . (1)解不等式 ; (2)已知 ,若 恒成立,求实数 的取值范围. 【解析】(1)不等式 可化为: ① 当 时,①式为 ,解得 ;当 时,①式为 ,解 得 ;当 时,①式为 ,无解.综上所述,不等式 的解集为 . 【备考知识梳理】 1.不等式证明的方法 (1)比较法:①求差比较法: 知道 0a b a b , 0a b a b ,因此要证明 a b 只要证明 0a b 即可,这种方法称为求 差比较法. ②求商比较法:由 0 1aa b b 且 0, 0a b ,因此当 0, 0a b 时,要证明 a b ,只要证明 1a b 即可,这种方法称为求商比较法. (2)综合法: 利用某些已经证明过的不等式和不等式的性质,推导出所要证明的不等式,这种方法叫综合法.即“由因导 果”的方法. (3)分析法: 证明不等式时,有时可以从求证的不等式出发,分析使这个不等式成立的充分条件,把证明不等式转化为 判定这些充分条件是否具备的问题,如果能够肯定这些充分条件都已经具备,那么就可以判定原不等式成 立,这种方法叫作分析法.即“执果索因”的方法. (4)反证法和放缩法: ①先假设要证的命题不成立,以此为出发点,结合已知条件,应用公理、定义、定理、性质等,进行正确 的推理,得到和命题的条件(或已证明的定理、性质、明显成立的事实等)矛盾的结论,以说明假设不正确, 从而证明原命题成立,这种方法叫作反证法. ②证明不等式时,通过把不等式中的某些部分的值放大或缩小,简化不等式,从而达到证明的目的,这种 方法叫作放缩法. 2.几个常用基本不等式 (1)柯西不等式: ①柯西不等式的代数形式:设 1 2 1 2, , ,a a b b 均为实数,则 22 2 2 2 1 2 1 2 1 1 2 2a a b b a b a b (当且仅当 1 2 1 2 a a b b 时,等号成立). ②柯西不等式的向量形式:设 , 为平面上的两个向量,则 . ③二维形式的三角不等式:设 1 2 1 2, , ,x x y y R ,那么 2 22 2 2 2 1 1 2 2 1 2 1 2x y x y x x y y . ④柯西不等式的一般形式:设 1 2 1 2, , , , , , ,n na a a b b b 为实数,则 22 2 2 2 2 2 1 2 1 2 1 1 2 2n n n na a a b b b a b a b a b ,当且仅当 1 2 1 2 n n aa a b b b 时,等 号成立. (2)平均值不等式: 定理:如果 , ,a b c 为正数,则 3 3 a b c abc ,当且仅当 a b c 时,等号成立. 我们称 3 a b c 为正数 , ,a b c 的算术平均值,3 abc 为正数 , ,a b c 的几何平均值,定理中的不等式为三个正 数的算术—几何平均值不等式,简称为平均值不等式. 一般形式的算术—几何平均值不等式:如果 1 2, , , na a a 为 n 个正数,则 1 2 1 2 n n n a a a a a an , 当且仅当 1 2 na a a 时,等号成立. 3.易错点:使用柯西不等式或平均值不等式时易忽视等号成立的条件. 易混淆分析法与综合法,分析法是执果索因,综合法是由因导果. 【规律方法技巧】 1. 绝对值不等式的证明:含绝对值不等式的证明题主要分两类:一类是比较简单的不等式,往往可通过公 式法、平方法、换元法等去掉绝对值转化为常见的不等式证明题,或利用绝对值三角不等式性质定理: a b a b a b ,通过适当的添、拆项证明;另一类是综合性较强的函数型含绝对值的不等式, 往往可考虑利用一般情况成立则特殊情况也成立的思想,或利用一元二次方程的根的分布等方法来证明. 2. 利用柯西不等式证明不等式:使用柯西不等式证明的关键是恰当变形,化为符合它的结构形式,当一个 式子与柯西不等式的左边或右边具有一致形式时,就可使用柯西不等式对这个式子进行缩小或放大,从而 证得问题.利用柯西不等式求最值的一般结构为: 22 2 2 2 1 2 2 2 2 1 2 1 1 1 1 1 1n n a a a na a a ,在使用柯西不等式时,要注意右边为常 数且应注意等号成立的条件. 3.放缩法证明不等式的技巧 (1)放缩法原理简单,但放缩技巧性强,而且应用广泛,常用的放缩法有增项、减项,利用分式的性质、函 数的性质、不等式的性质等.其理论依据是不等式的传递性,使用此方法时要注意把握放大或缩小的度, 既不能放的过小,也不能放过了头.常见的放缩依据和技巧是不等式的传递性.缩小分母、扩大分子,分 式值增大;缩小分子、扩大分母,分式值减小;每一次缩小其和变小,但需大于所求;每一次扩大其和变 大,但需小于所求,即不能放缩不够或放缩过头. (2)常见的放缩技巧有: ① 2 1 1 1 1 1k k k k k ( 2,k k N ); ② 2 2 2 1 2 1k k k k k 2 k-1+ k > 2 2 k > 2 k+ k+1 ( ≥2,且 ∈N ). 4.对于多项式的大小比较问题通常可以用比较法,而比较法中最常用的是作差法和作商法.作差法中作差后 的关键是对差的符号进行判断,通常运用配方、因式分解等方法,作商法要注意两式的符号. 用作商法证明不等式应注意: 1 0 A A BB B . 1 0 A A BB B .因此,用作商法必须先判定符号. 5.应用不等时注意以下几点: (1)使用均值不等式求最值时,必须满足“一正、二定、三相等”的条件,且注意变形配凑技巧. (2)基本不等式及其变式中的条件要准确把握.如 2 2 2a b ab ( ,a b R ), 2a b ab ( ,a b R )等. (3)含绝对值三角不等式: a b a b a b a b 中等号成立的条件应注意 a b a b 中 0ab ,而 a b a b 中 0ab 等. (4)分析法证明不等式的每一步都是寻求不等式成立的充分条件. (5)换元法证明不等式时要注意换元后新元的取值范围忽视它会导致错误结论或无法进行下去. (6)用数归纳法证明不等式时,关键是配凑合适的项便于应用归纳假设. (7)应用柯西不等式关键是分析、观察所给式子的特点,从中找出柯西不等式的必备形式特点及等号成立 的条件. (8)柯西不等式及排序不等式中 ,i ia b (i=1,2,…,n)均为实数,而平均值不等式中 ia 为正数. 【考点针对训练】 1. 【云南省昆明市 2018 届适应性检测】已知 , , , , ,a b c m n p 都是实数,且 2 2 2 2 2 21, 1a b c m n p . (Ⅰ)证明 1am bn cp ; (Ⅱ)若 0abc ,证明 4 4 4 2 2 2 1m n p a b c . 【解析】(Ⅰ)因为 am bn cp am bn cp , 2 2 2 2 2 21, 1a b c m n p 所以 2 2 2 2 2 2 2 2 2 2 2 2 12 2 2 2 a m b n c p a b c m n pam bn cp . 即 1am bn cp . (Ⅱ)因为 2 2 2 2 2 21, 1a b c m n p ,所以 4 4 4 4 4 4 2 2 2 2 2 2 2 2 2 m n p m n p a b ca b c a b c 22 2 2 22 2 2 1m n pa b c m n pa b c . 所以 4 4 4 2 2 2 1m n p a b c . 2. 【2018 届第三次全国大联考】已知函数 . (1)若 ,求满足条件的实数 的值所组成的集合 ; (2)若 ,求证: . 【应试技巧点拨】 1.绝对值三角不等式定理的应用 对于绝对值三角不等式定理: a - b ≤ a±b ≤ a + b ,要从以下两个方面深刻理解: (1)两端的等号成立的条件在解题时经常用到,特别是用此定理求函数的最大(小)值时. (2)该定理可以推广为 a+b+c≤ a + b + c ,也可强化为 a - b ≤ a±b ≤ a + b ,它们经常用于含绝 对值的不等式的推证. 例 1 f(x)= 3-x + x-2 的最小值为________. 解析:∵ 3-x + x-2 ≥ 3-x+(x-2) =1, ∴f(x)min=1. 2.绝对值不等式的解法 (1)形如 x+a ± x-b ≥c 不等式的解法常用零点分段讨论法,其步骤为: ①求零点;②划分区间、去绝对值号;③分别解去掉绝对值的不等式;④取每个结果的并集,特别注意在 分段时不要漏掉区间的端点值. (2)上述不等式也可用 x-a1 ± x-a2 的几何意义去求解集. 3.绝对值不等式的证明 含绝对值不等式的证明题主要分两类:一类是比较简单的不等式,往往可通过公式法、平方法、换元法等 去掉绝对值转化为常见的不等式证明题,或利用绝对值三角不等式性质定理: a - b ≤ a±b ≤ a + b , 通过适当的添、拆项证明;另一类是综合性较强的函数型含绝对值的不等式,往往可考虑利用一般情况成 立则特殊情况也成立的思想,或利用一元二次方程的根的分布等方法来证明. 4.利用柯西不等式证明不等式 使用柯西不等式证明的关键是恰当变形,化为符合它的结构形式,当一个式子与柯西不等式的左边或右边 具有一致形式时,就可使用柯西不等式对这个式子进行缩小或放大,从而证得问题. 1.【广东省珠海市 2018 届质量检测】已知函数 . (1)解不等式 ; (2)已知 ,若不等式 恒成立,求实数 的取值范围. 2. 【山东省菏泽市 2018 届一模拟】已知函数 . (1)求不等式 的解集; (2)设 ,若对任意 不等式 成立,求实数 m 的取值范围. 【 解 析 】( 1 ) 因 为 , 所 以 即 为 , 整 理 得 .讨论:①当 时, ,即 ,解得 . 又 ,所以 .②当 时, ,即 ,解得 . 又 ,所以 .综上,所求不等式的解集为 . (2)据题意,得 对任意 恒成立,所以 恒成立.又 因为 ,所以 .所以 ,解得 .所以所 求实数 m 的取值范围是 . 3. 【四川省成都市 2018 届二诊模拟】已知函数 . (1)解不等式 (2)若 且 恒成立,求实数 的取值范围. 4. 【广东省江门市 2018 届 3 月模拟】已知函数 , . (Ⅰ)解不等式 ; , , (Ⅱ)若对 ,都存在 ,使得 ,求实数 的取值范围. 【解析】(Ⅰ)依题意, , , (Ⅱ)函数 的值域为 ,设函数 的值域为 ,依题意, , 时, , 此时 ,不合题意 时, ,此时 ,解 得 , 时, ,此时 ,解 得 ,综上所述, 实数 的取值范围为 5.【安徽省江南十校 2018 届 3 月联考】已知函数 , . (1)当 ,解不等式 ; (2)求证: . 6.【江西省南昌市 2018 届一模】已知 . (1)当 时,求不等式 的解集; (2)对于任意实数 ,不等式 成立,求实数 的取值范围. 【解析】(1)当 时, , 得 ; 得 ; 得 ,所以 的解集为 . (2)对于任意实数 ,不等式 成立,即 恒成立,又因为 ,要使原不等式恒成立,则只需 , 当 时,无解;当 时, ,解得 ;当 时, ,解得 . 所以实数 的取值范围是 . 7.【福建省莆田市 2018 届质量检测(3 月)】已知函数 . (1)当 时,求不等式 的解集; (2)若 ,求 的取值范围. 【解析】(1)当 时,不等式 ,即 .可得 ,或 , 或 .解得 .所以不等式的解集为 . (2)因为 .当且仅当 时, 取得最小值 . 又因为对任意的 恒成立,所以 ,即 ,故 , 解得 .所以 的取值范围为 . 8.【贵州省黔东南州 2018 届第一次模拟】设 . (Ⅰ)求不等式 的解集; (Ⅱ) , ,求实数 的取值范围. 9.【重庆市 2018 届适应性模拟】设 2 - 1f x x a x . (1)当 a=2 时,求不等式 1f x 的解集; (2)若 a>0,b>0,c>0 且 ab+bc+ac=1,求证:当 xR 时,f(x) 2 2 2b 2c a 【解析】(1)解:当 2a 时, 5 { 2 3 5 f x x , , , 1 1 4 4 x x x , , , ①当 1x 时, 5 1f x ,不等式 无 解;②当 1 4x 时,可得 2 3 1f x x ,解得 1x ,∴1 4x ;③当 4x 时, 5 1f x 恒成立,∴ 4x .综上得 1x .∴不等式 1f x 的解集为 1, . (2)证明:当 x R 时, 2 21 1f x x a x x a x 2 21 1a a ,而 2 2 2 2 2 2 2+ 2 1 1b c a a b c a 2 2 2 2 2 21= + + + 12 a b b c c a 1 2 2 2 1 1 02 ab bc ac ab bc ac ,当且仅当 3 3a b c 时等号成立,∴ 2 2 2 22 +1b c a a ,∴当 x R 时, 2 2 2 21 2f x a b c a . 10.【广东省深圳市 2018 届第一次调研】已知 0a , 0b ,且 2 2 2a b . (1)若 2 2 1 4 2 1 1x xa b 恒成立,求 x 的取值范围; (2)证明: 5 51 1 4a ba b . 另解:由柯西不等式,可得 2 22 2 5 5 25 5 2 22 21 1 1 1 4a b a b a ba b a b . 11.【湖北武汉市 2017 届高三第三次模拟】已知函数 2 1 3 2f x x x ,且不等式 5f x 的解集 为 4 3{ | }5 5 a bx x , a , Rb . (1)求 a , b 的值; (2)对任意实数 x ,都有 2 3 5x a x b m m 成立,求实数 m 的最大值. 【解析】(1)若 1 2x ,原不等式可化为 2 1 3 2 5x x ,解得 4 5x ,即 4 1 5 2x ; 12.【2017 届福建省泉州市高三 3 月质量检测】已知函数 1 2 4f x x x . (1)解关于 x 的不等式 9f x ; (2)若直线 y m 与曲线 y f x 围成一个三角形,求实数 m 的取值范围,并求所围成的三角形面积的 最大值. 【解析】(1) 3 3, 1 1 2 4 { 5, 1 2 3 3, 2 x x f x x x x x x x . ①当 1x 时,由不等式 3 3 9x ,解得 2x .此时原不等式的解集是: { | 2 1x x . ②当 1 2x 时,由不等式 5 9x ,解得 4x .此时原不等式的解集是: { | 1 2}x x . ③当 2x 时,由不等式3 3 9x ,解得 4x ,此时原不等式的解集是: { | 2 4}x x . 综上可得原不等式的解集为 2,4 . (2)由(1)可得,函数 f x 的图像是如下图所示的折线图.因为 min1 6, 2 3f f x f , 故当 3 6m 时,直线 y m 与曲线 y f x 围成一个三角形,即 m 的范围是 3,6 . 且当 6m 时, max 1 3 1 6 3 62S . 13. 【2017 届安徽省宣城市高三第二次调研】已知 1f x ax ,若实数 0a ,不等式 3f x 的 解集是{ | 1 2}x x . (1)求 a 的值; …… (2)若 3 f x f x k 存在实数解,求实数 k 的取值范围. 14.【河南省新乡市 2017 届高三第三次模拟】已知不等式 x m x 的解集为 1, . (1)求实数 m 的值; (2)若不等式 5 1 21 1a m a x x x x 对 0,x 恒成立,求实数 a 的取值范围. 【解析】(1)由 x m x 得 2 2x m x ,即 22mx m ,而不等式 x m x 的解集为 1, , 则1是方程 22mx m 的解,解得 2( 0m m 舍去). (2) 2,m 不等式 5 1 21 1a m a x x x x 对 0,x 恒成立等价于,不等式 5 1 2 2a x x a 对 0,x 恒成立,设 2 1,0 21 2 { 3, 2 x xf x x x x , 则 1,3 . 2 3, 5 1, 1 4f x a a a . 15.【2017 届陕西省咸阳市高三二模】已知函数 4 ( 0)f x m x m ,且 2 0f x 的解集为 3, 1 . (1)求 m 的值; (2)若 , ,a b c 都是正实数,且 1 1 1 2 3 ma b c ,求证: 2 3 9a b c . 【一年原创真预测】 1. 设函数 ( ) 2 1 ,f x x x R . (1)解不等式 ( ) 5 ( 1)f x f x ; (2)已知不等式 ( ) ( 1) | |f x f x x a 的解集为 M ,若 1( ,1)2 M ,求实数 a 的取值范围. 【入选理由】本题主要考查绝对值不等式的解法、三角不等式的应用等基础知识,意在考查等价转化的能 力、逻辑思维能力、运算求解能力,以及分类讨论的思想与转化思想.本题突出考查了绝对值不等式的解 法,三角不等式的灵活应用,主要考查的是对基本知识的理解与运用,基础性强,难度不大,故选此题. 2. 已知函数 ( ) | 1|f x x . (1)若 0x R ,使不等式 ( 2) ( 3)f x f x t 成立,求满足条件的实数t 的取值集合T ; (2)若二次函数 2 2 3y x x 与函数 2 ( ) ( 2)y m f x f x 的图象恒有公共点,求实数 m 的取值范围. 【解析】(1) 由已知得 1, 1 ( 2) ( 3) 1 2 2 3,1 2 1, 2 x f x f x x x x x x ,则 1 1f x , 由于 0x R ,使不等式 1 2x x t 成立,所以 1t ,即 | 1t T t t . (2)易知二次函数 22 2 3 1 2y x x x 在 1x 处取得最小值,为 2 .因为 3 1 , 1 2 ( ) ( 2) 3 , 1 1 3 1, 1 x m x y m f x f x x m x x m x 在 1x 处取得最大值 2m ,所以要使二次函数 2 2 3y x x 与函数 2 ( ) ( 2)y m f x f x 的图象恒有公共点,只需 2 2m ,即 4m . 【入选理由】本题主要考查绝对值不等式的解法,存在性问题等基础知识,意在考查生综合分析问题、解 决问题的能力以及运算求解能力、逻辑思维能力,考查化归与转化的数思想.本题突出考查了绝对值不等 式的解法,主要考查的是对基本知识的理解与运用,基础性强,难度不大,故选此题. 3. 已知函数 2 1f x x x . (1)解不等式 0f x x ; (2)若关于 x 的不等式 2 2f x a a 在 R 上的解集为 R ,求实数 a 的取值范围. 【入选理由】本题主要考查绝对值不等式的解法,恒成立问题等基础知识,意在考查生综合分析问题、解 决问题的能力以及运算求解能力、逻辑思维能力,考查化归与转化的数思想.本题主要考查的是对基本知 识的理解与运用,基础性强,难度不大,故选此题. 4. 已知不等式 2 2 2 2x x 的解集为 M . (Ⅰ)求集合 M ; (Ⅱ)已知t 为集合 M 中的最小正整数,若 1, 1, 1a b c ,且 1 1 1a b c t ,求证: 8abc . 【解析】(Ⅰ)设 2 2 2f x x x ,则 4, 1 3 , 1 2 4, 2 x x f x x x x x ,当 1x 时,由 4 2x ,得 6x , 6x ∴ ;当 1 2x 时,由3 2x ,得 2 3x , 2 23 x ∴ ;当 2x 时,由 4 2x ,得 2x , 2x ∴ .综上所述,集合 M 为 2| 63x x x 或 . (Ⅱ)由(Ⅰ)知 1t ,则 1 1 1 1a b c t . 因为 1, 1, 1a b c ,所以 1 0, 1 0, 1 0a b c ,则 1 1 2 1 0a a a ,(当且仅当 2a 时等号成立), 1 1 2 1 0b b b ,(当且仅当 2b 时等号成立), 1 1 2 1 0c c c ,(当且仅当 2c 时等号成立),则 8 1 1 1 8abc a b c (当且仅当 2a b c 时等号成立),即 8abc . 【入选理由】本题主要考查绝对值不等式的解法、不等式的证明,意在考查运算求解能力、逻辑推理能力、 分类讨论与等价转化的思想.本题主要考查的是对基本知识的理解与运用,基础性强,难度不大,故选此 题. 5. 设函数 ( ) | 2 | | 3|f x x x . (1)求不等式 ( ) 3f x 的解集; (2)若不等式 ( ) 3f x a 对任意 xR 恒成立,求实数 a 的取值范围. 【入选理由】本小题主要考查绝对值不等式的解法,恒成立问题等基础知识,意在考查生综合分析问题、 解决问题的能力以及运算求解能力.本题突出考查了绝对值不等式的解法,主要考查的是对基本知识的理 解与运用,基础性强,难度不大,故选此题.查看更多