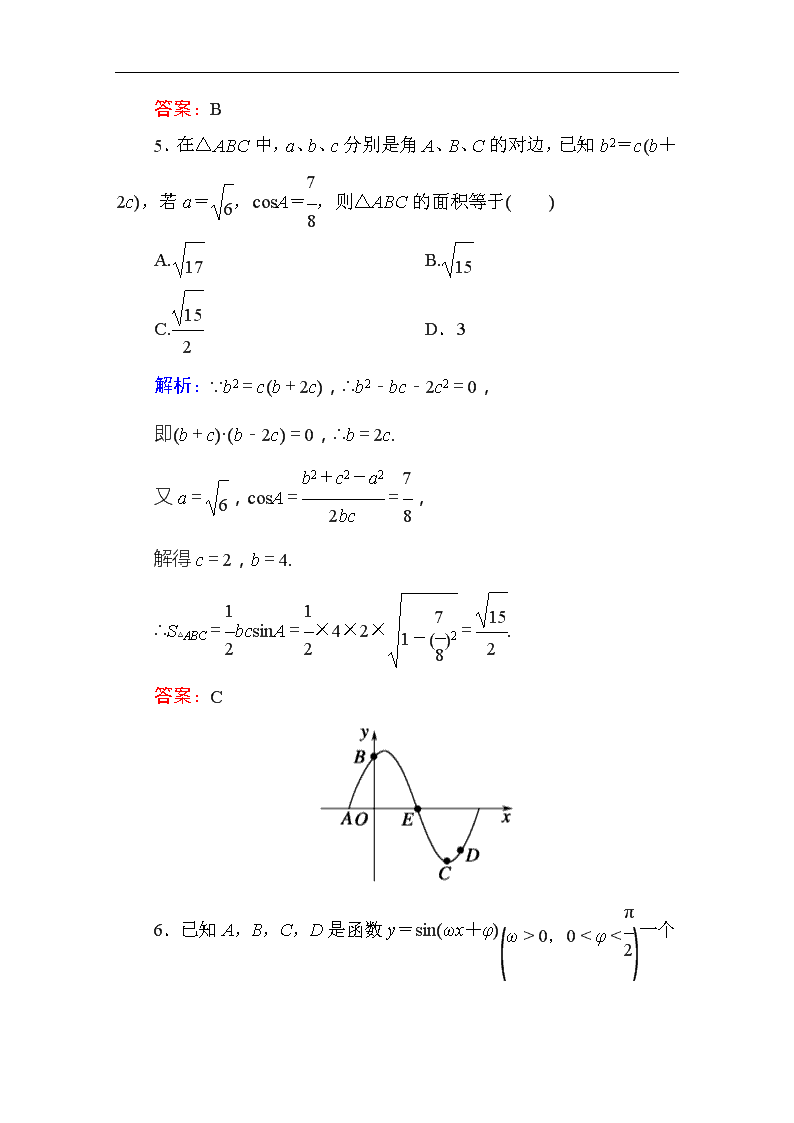人教版高三数学总复习课时作业26
课时作业26 三角函数高考热点追踪
一、选择题
1.“φ=π”是“曲线y=sin(2x+φ)过坐标原点”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
解析:当φ=π时,y=sin(2x+φ)=-sin2x过原点.当曲线过原点时,φ=kπ,k∈Z,不一定有φ=π.∴“φ=π”是“曲线y=sin(2x+φ)过原点”的充分不必要条件.
答案:A
2.已知向量a=(2,sinx),b=(cos2x,2cosx),则函数f(x)=a·b的最小正周期是( )
A. B.π
C.2π D.4π
解析:f(x)=2cos2x+2sinxcosx=1+cos2x+sin2x
=1+sin,T==π.
答案:B
3.若tanα+=,α∈(,),则sin(2α+)的值为( )
A.- B.
C. D.
解析:由tanα+=得+=
∴=,∴sin2α=.
∵α∈(,),∴2α∈(,π),∴cos2α=-.
∴sin(2α+)=sin2αcos+cos2αsin
=×(-)=-.
答案:A
4.若函数f(x)=(1+tanx)cosx,0≤x<,则f(x)的最大值为( )
A.1 B.2
C.+1 D.+2
解析:依题意,得f(x)=cosx+sinx=2sin(x+),
当0≤x<时,≤x+<,
f(x)的最大值是2.
答案:B
5.在△ABC中,a、b、c分别是角A、B、C的对边,已知b2=c(b+2c),若a=,cosA=,则△ABC的面积等于( )
A. B.
C. D.3
解析:∵b2=c(b+2c),∴b2-bc-2c2=0,
即(b+c)·(b-2c)=0,∴b=2c.
又a=,cosA==,
解得c=2,b=4.
∴S△ABC=bcsinA=×4×2×=.
答案:C
6.已知A,B,C,D是函数y=sin(ωx+φ)一个周期内的图象上的四个点,如图所示,A,B为y轴上的点,C为图象上的最低点,E为该函数图象的一个对称中心,B与D关于点E对称,在x轴上的投影为,则ω,φ的值为( )
A.2, B.,
C.2, D.,
解析:
由在x轴上的投影为,知OF=,
又A,所以AF===,所以ω=2.同时函数图象可以看成是由y=sin2x的图象向左平移而来,故可知==,故φ=.
答案:A
二、填空题
7.(2014·山东卷)函数y=sin2x+cos2x的最小正周期为______.
解析:原式=sin2x+=sin+.
∴周期T==π.
答案:π
8.设△ABC的内角A,B,C所对边的长分别为a,b,c.若b+c=2a,3sinA=5sinB,则角C=________.
解析:由已知条件和正弦定理得:3a=5b,且b+c=2a,
则a=,c=2a-b=
cosC==-,又0
0时,cos=,y取得最大值为a+3,
∴a+3=4,∴a=2.
当a<0时,cos=-1,y取得最大值为-a+3,
∴-a+3=4,∴a=-1.
综上可知,实数a的值为2或-1.
答案:2或-1
三、解答题
10.(2014·北京卷)如右图,在△ABC中,∠B=,AB=8,点D在BC边上,且CD=2,cos∠ADC=.
(1)求sin∠BAD;
(2)求BD,AC的长.
解:(1)在△ADC中,因为cos∠ADC=,所以sin∠ADC=.
所以sin∠BAD=sin(∠ADC-∠B)
=sin∠ADCcosB-cos∠ADCsinB
=×-×=.
(2)在△ABD中,由正弦定理得
BD===3.
在△ABC中,由余弦定理得
AC2=AB2+BC2-2AB·BC·cosB
=82+52-2×8×5×=49.
所以AC=7.
11.已知△ABC中,角A,B,C的对边分别为a,b,c,tanA·tanB-(tanA+tanB)=,且c=.
(1)求角C的大小;
(2)求△ABC周长的取值范围.
解:(1)由tanA·tanB-(tanA+tanB)=,
得tanA·tanB-=tanA+tanB,
所以tan(A+B)==-.
在△ABC中,A+B=,所以C=.
(2)由c=及正弦定理,得===2,可得a=2sinA,b=2sinB,
所以a+b+c=2(sinA+sinB)+=2[sinA+sin(-A)]+=cosA+3sinA+=2sin(A+)+.
因为00)的一段图象如图所示,△ABC的顶点A与坐标原点O重合,B是f(x)的图象上一个最低点,C在x轴上,若内角A,B,C所对边长分别为a,b,c,且△ABC的面积S满足12S=b2+c2-a2,将f(x)的图象向左平移一个单位得到g(x)的图象,则g(x)的表达式为( )
A.g(x)=cosx B.g(x)=-cosx
C.g(x)=sin D.g(x)=sin
解析:
自点B向x轴作垂线,D为垂足.
由已知,12S=b2+c2-a2,
即12×bcsin∠BAC=b2+c2-a2,
∴3sin∠BAC==cos∠BAC,
∴tan∠BAC=.
∴AD=3,即T=3,T=4,=4,ω=,
f(x)=sinx.
将f(x)的图象向左平移一个单位得到g(x)=sin(x+1)的图象,即g(x)=cosx,故选A.
答案:A
3.如图所示,某电力公司为保护一墙角处的电塔,计划利用墙OA,OB,再修建一长度为AB的围栏,围栏的造价与AB的长度成正比.现已知墙角AOB的度数为120°,当△AOB的面积为时,就可起到保护作用.则当围栏的造价最低时, ∠ABO=( )
A.30° B.45°
C.60° D.90°
解析:只要AB的长度最小,围栏的造价就最低.设OA=a,OB=b,则由余弦定理得AB2=a2+b2-2abcos120°=a2+b2+ab≥2ab+ab=3ab(当且仅当a=b时取等号),又S△AOB=absin120°=,所以ab=4.故AB2≥12,即AB的最小值为2.由a=b及3ab=12,得a=b
=2.由正弦定理得sin∠ABO==×=.故∠ABO=30°,故选A.
答案:A
4.将函数f(x)=2sin(ωx+φ)(ω>0,0<φ<π)的图象向右平移个单位长度后得到g(x)的图象,已知g(x)的部分图象如图所示,该图象与y轴相交于点F(0,1),与x轴相交于点P,Q,点M为最高点,且△MPQ的面积为.
(1)求函数g(x)的解析式;
(2)在△ABC中,a,b,c分别是角A,B,C的对边,g(A)=1,且b=,求△ABC面积的最大值.
解:(1)由题意可知g(x)=2sin.
由于S△MPQ=·2·|PQ|=,
则|PQ|==,∴T=π,即ω=2.
又由于g(0)=2sin=1,
且-<φ-<,则φ-=,∴φ=.
即g(x)=2sin=2sin.
(2)g(A)=2sin=1,2A+∈,则2A+=,∴A=.
由余弦定理得b2+c2-2bccosA=a2=5,
∴5=b2+c2-bc≥bc.
∴S△ABC=bcsinA≤,当且仅当b=c=时,等号成立,故S△ABC的最大值为.