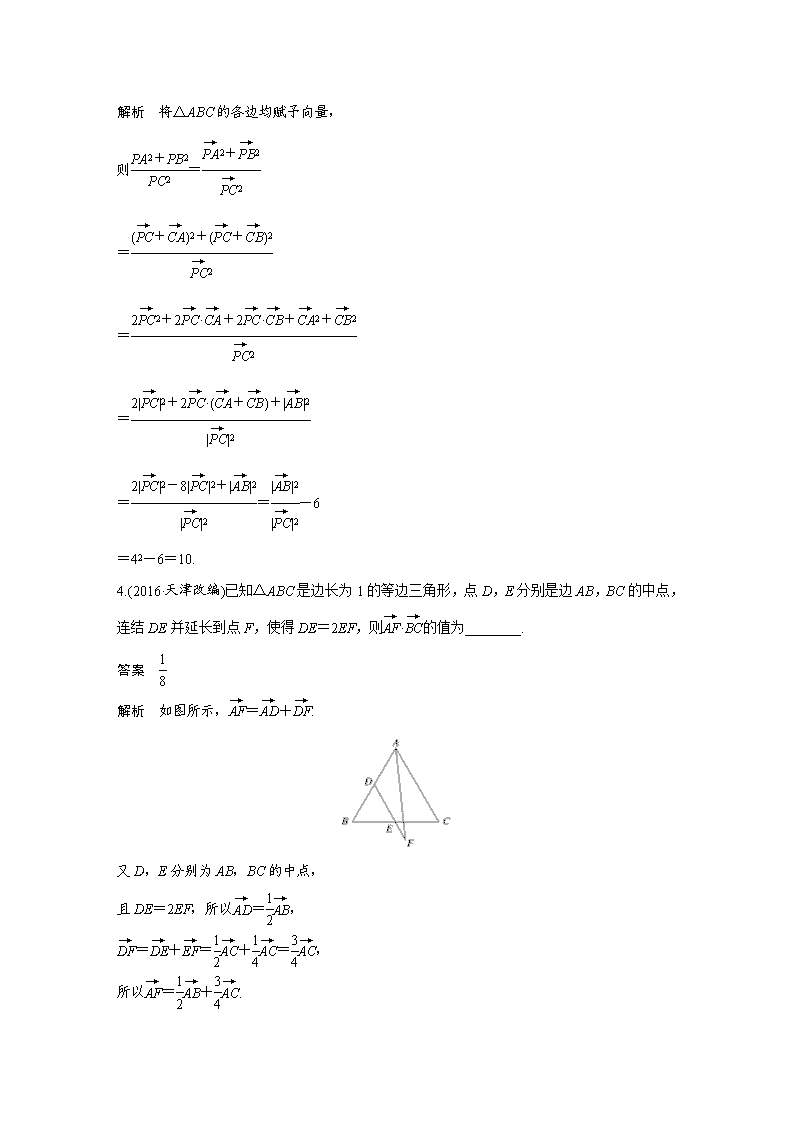【数学】2018届一轮复习人教A版高考专题突破二高考中的三角函数与平面向量问题学案
1.(2016·江苏镇江中学质检)已知函数y=2sin ωx(ω>0)在上的最大值为,则ω的值是________.
答案 1
解析 由题意得>,即T>π,从而>π,
即0<ω<2,故函数在x=时取得最大值,
即2sin(ω)=,也即sin(ω)=,
又ω∈(0,),故ω=,
解得ω=1.
2.在△ABC中,AC·cos A=3BC·cos B,且cos C=,则A=________.
答案 45°
解析 由题意及正弦定理得sin Bcos A=3sin Acos B,
∴tan B=3tan A,∴0°<A<90°,0°
0)在区间(-1,0)上有且仅有一条平行于y轴的对称轴,则ω的最大值是________.
答案
解析 令ωπx-=kπ+,则得x=(k∈Z),
∴当k=-1时,得y轴左侧第1条对称轴为-;当k=-2时,得y轴左侧第2条对称轴为-,因此-1<-<0且-1≥-,解得<ω≤,故ωmax=.
题型一 三角函数的图象和性质
例1 已知函数f(x)=sin(ωx+)+sin(ωx-)-2cos2,x∈R(其中ω>0).
(1)求函数f(x)的值域;
(2)若函数y=f(x)的图象与直线y=-1的两个相邻交点间的距离均为,求函数y=f(x)的单调增区间.
解 (1)f(x)=sin ωx+cos ωx+sin ωx-cos ωx-(cos ωx+1)
=2(sin ωx-cos ωx)-1=2sin(ωx-)-1.
由-1≤sin(ωx-)≤1,
得-3≤2sin(ωx-)-1≤1,
所以函数f(x)的值域为[-3,1].
(2)由题设条件及三角函数图象和性质可知,y=f(x)的周期为π,所以=π,即ω=2.
所以f(x)=2sin(2x-)-1,
再由2kπ-≤2x-≤2kπ+(k∈Z),
解得kπ-≤x≤kπ+(k∈Z).
所以函数y=f(x)的单调增区间为
[kπ-,kπ+](k∈Z).
思维升华 三角函数的图象与性质是高考考查的重点,通常先将三角函数化为y=Asin(ωx+φ)+k的形式,然后将t=ωx+φ视为一个整体,结合y=sin t的图象求解.
已知函数f(x)=5sin xcos x-5cos2x+(其中x∈R),求:
(1)函数f(x)的最小正周期;
(2)函数f(x)的单调区间;
(3)函数f(x)图象的对称轴和对称中心.
解 (1)因为f(x)=sin 2x-(1+cos 2x)+
=5(sin 2x-cos 2x)=5sin(2x-),
所以函数的周期T==π.
(2)由2kπ-≤2x-≤2kπ+(k∈Z),
得kπ-≤x≤kπ+ (k∈Z),
所以函数f(x)的单调增区间为
[kπ-,kπ+](k∈Z).
由2kπ+≤2x-≤2kπ+(k∈Z),
得kπ+≤x≤kπ+(k∈Z),
所以函数f(x)的单调减区间为
[kπ+,kπ+](k∈Z).
(3)由2x-=kπ+(k∈Z),得x=+(k∈Z),
所以函数f(x)的对称轴方程为x=+(k∈Z).
由2x-=kπ(k∈Z),得x=+(k∈Z),
所以函数f(x)的对称中心为(+,0)(k∈Z).
题型二 解三角形
例2 (2016·苏北四市期中)在△ABC中,已知角A,B,C所对的边分别为a,b,c,且tan B=2,tan C=3.
(1)求角A的大小;
(2)若c=3,求b的长.
解 (1)因为tan B=2,tan C=3,A+B+C=π,
所以tan A=tan[π-(B+C)]=-tan(B+C)
=-=-=1,
又A∈(0,π),所以A=.
(2)因为tan B==2,且sin2B+cos2B=1,
又B∈(0,π),所以sin B=,
同理可得,sin C=.
由正弦定理得b===2.
思维升华 根据三角形中的已知条件,选择正弦定理或余弦定理求解;在做有关角的范围问题时,要注意挖掘题目中隐含的条件,正确对结果进行取舍.
(2016·无锡期中)在△ABC中,角A,B,C所对的边分别为a,b,c,已知bsin A=acos B.
(1)求角B的值;
(2)若cos Asin C=,求角A的值.
解 (1)因为=,所以bsin A=asin B,
又bsin A=acos B,
所以acos B=asin B,
即tan B=,所以角B=.
(2)因为cos Asin C=,
所以cos Asin(-A)=,
cos A(cos A+sin A)=cos2A+sin A·cos A
=·+sin 2A=,
所以sin(2A+)=-,
因为0c.已知·=2,cos B=,b=3,求:
(1)a和c的值;
(2)cos(B-C)的值.
解 (1)由·=2,得c·acos B=2.
又cos B=,所以ac=6.
由余弦定理,得a2+c2=b2+2accos B.
又b=3,所以a2+c2=9+2×2=13.
解得a=2,c=3或a=3,c=2.
因为a>c,所以a=3,c=2.
(2)在△ABC中,sin B== =,
由正弦定理,得sin C=sin B=×=.
因为a=b>c,所以C为锐角,
因此cos C== =.
于是cos(B-C)=cos Bcos C+sin Bsin C
=×+×=.
1.已知函数f(x)=Asin(x+),x∈R,且f()=.
(1)求A的值;
(2)若f(θ)+f(-θ)=,θ∈(0,),求f(-θ).
解 (1)∵f()=Asin(+)=Asin =A=,
∴A=.
(2)由(1)知f(x)=sin(x+),
故f(θ)+f(-θ)=sin(θ+)+sin(-θ+)=,
∴[(sin θ+cos θ)+(cos θ-sin θ)]=,
∴cos θ=,∴cos θ=.
又θ∈(0,),∴sin θ==,
∴f(-θ)=sin(π-θ)=sin θ=.
2.(2016·山东)设f(x)=2sin(π-x)sin x-(sin x-cos x)2.
(1)求f(x)的单调递增区间;
(2)把y=f(x)的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图象向左平移个单位,得到函数y=g(x)的图象,求g的值.
解 (1)f(x)=2sin(π-x)sin x-(sin x-cos x)2
=2sin2x-(1-2sin xcos x)=(1-cos 2x)+sin 2x-1
=sin 2x-cos 2x+-1
=2sin+-1.
由2kπ-≤2x-≤2kπ+(k∈Z),
得kπ-≤x≤kπ+(k∈Z).
所以f(x)的单调递增区间是(k∈Z).
(2)由(1)知f(x)=2sin+-1,
把y=f(x)的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变).得到y=2sin+-1的图象.
再把得到的图象向左平移个单位,
得到y=2sin x+-1的图象,即g(x)=2sin x+-1.
所以g=2sin +-1=.
3.(2016·江苏南京学情调研)如图,在平面直角坐标系xOy中,以x轴正半轴为始边的锐角α和钝角β的终边分别与单位圆交于点A,B.若点A的横坐标是,点B的纵坐标是.
(1)求cos(α-β)的值;
(2)求α+β的值.
解 (1)因为锐角α的终边与单位圆交于点A,且点A的横坐标是,所以,由任意角的三角函数的定义可知,cos α=,从而sin α==.因为钝角β的终边与单位圆交于点B,且点B的纵坐标是,
所以sin β=,从而cos β=-=-.
cos(α-β)=cos αcos β+sin αsin β
=×(-)+×=-.
(2)sin(α+β)=sin αcos β+cos αsin β
=×(-)+×=.
因为α为锐角,β为钝角,故α+β∈(,),
所以α+β=.
4.(2016·江苏仪征中学期初测试)设函数f(x)=Asin(ωx+φ) (A>0,ω>0,-<φ<,x∈R)的部分图象如图所示.
(1)求函数y=f(x)的解析式;
(2)当x∈[-,]时,求f(x)的取值范围.
解 (1)由图象知,A=2,又=-=,ω>0,
所以T=2π=,得ω=1.所以f(x)=2sin(x+φ),将点(,2)代入,得+φ=+2kπ(k∈Z),
即φ=+2kπ(k∈Z),又-<φ<,所以φ=.
所以f(x)=2sin(x+).
(2)当x∈[-,]时,x+∈[-,],
所以sin(x+)∈[-,1],即f(x)∈[-,2].
5.已知向量a=(ksin ,cos2),b=(cos ,-k),实数k为大于零的常数,函数f(x)=a·b,x∈R,且函数f(x)的最大值为.
(1)求k的值;
(2)在△ABC中,a,b,c分别为内角A,B,C所对的边,若
查看更多