- 2021-06-16 发布 |
- 37.5 KB |
- 12页
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2019届二轮复习小题专练 空间几何体的视图、表面积与体积作业(全国通用)
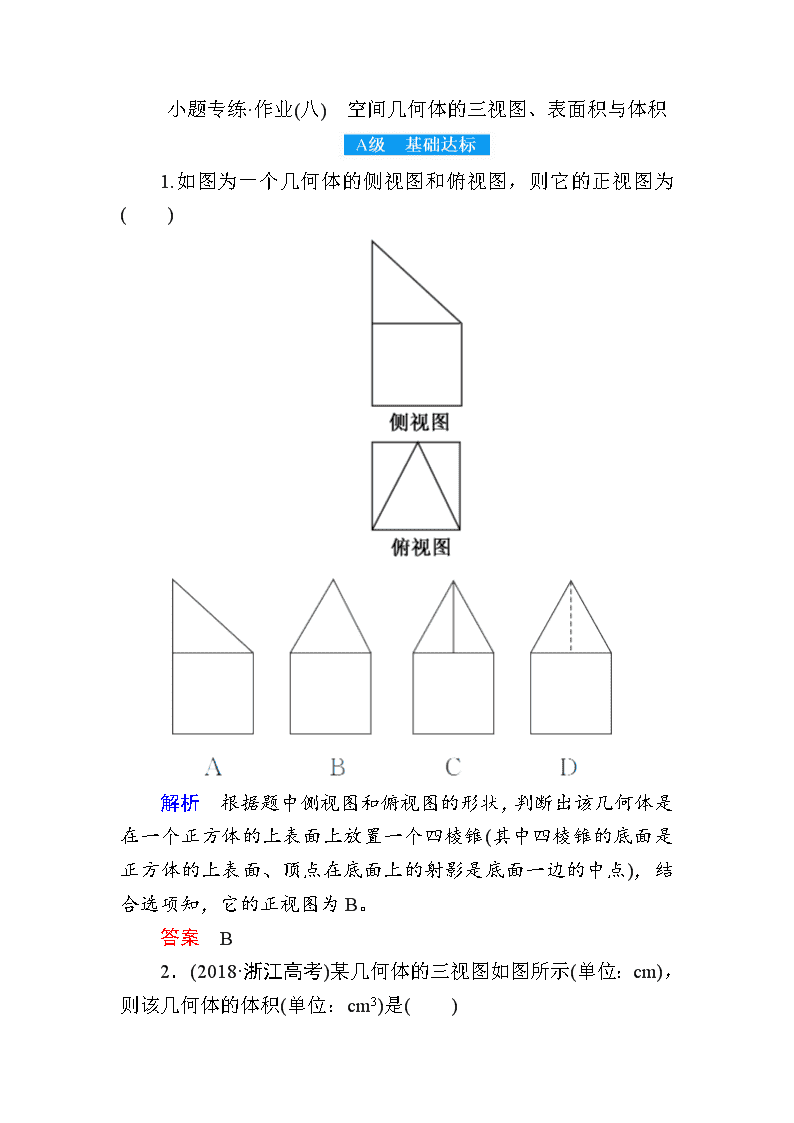
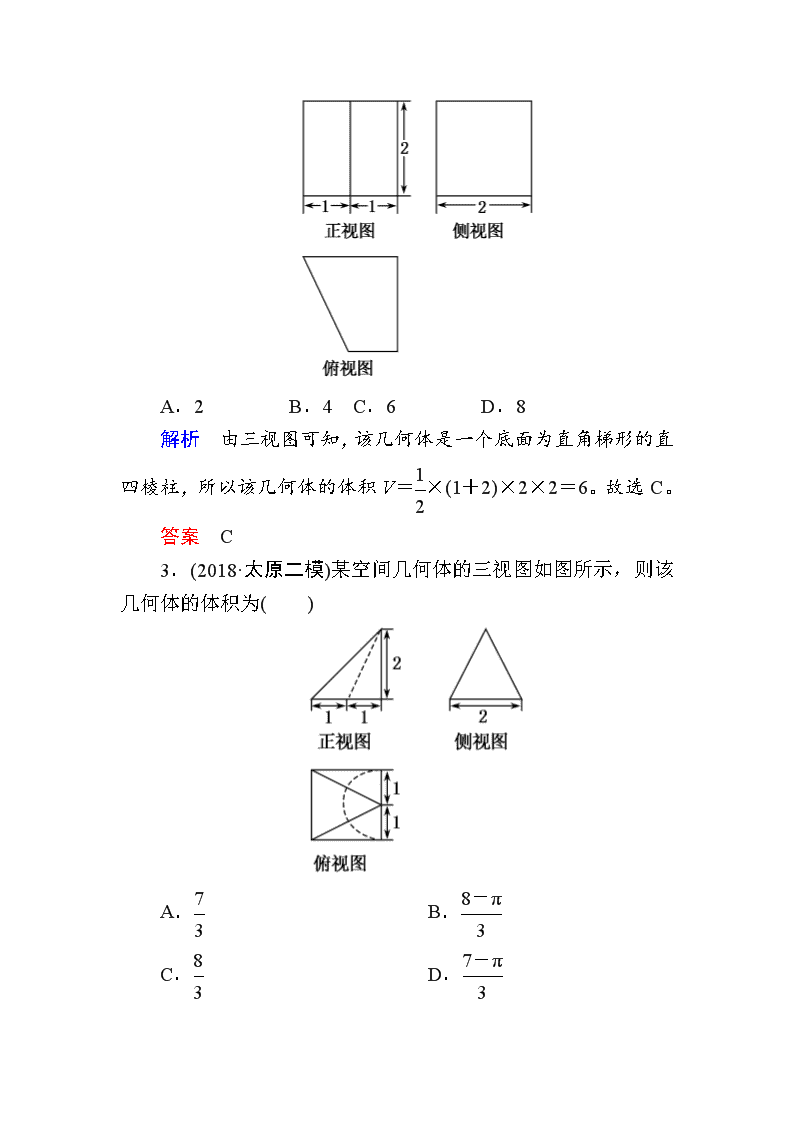
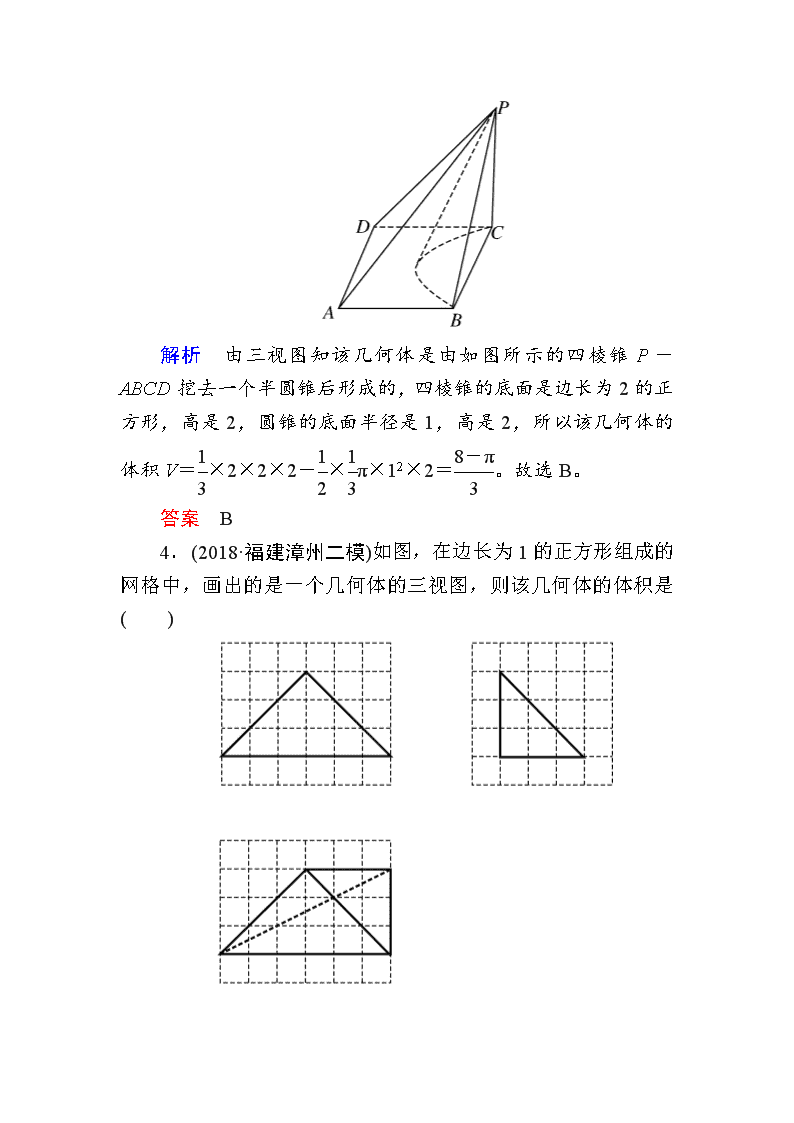
小题专练·作业(八) 空间几何体的三视图、表面积与体积 1.如图为一个几何体的侧视图和俯视图,则它的正视图为( ) 解析 根据题中侧视图和俯视图的形状,判断出该几何体是在一个正方体的上表面上放置一个四棱锥(其中四棱锥的底面是正方体的上表面、顶点在底面上的射影是底面一边的中点),结合选项知,它的正视图为B。 答案 B 2.(2018·浙江高考)某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm3)是( ) A.2 B.4 C.6 D.8 解析 由三视图可知,该几何体是一个底面为直角梯形的直四棱柱,所以该几何体的体积V=×(1+2)×2×2=6。故选C。 答案 C 3.(2018·太原二模)某空间几何体的三视图如图所示,则该几何体的体积为( ) A. B. C. D. 解析 由三视图知该几何体是由如图所示的四棱锥P-ABCD挖去一个半圆锥后形成的,四棱锥的底面是边长为2的正方形,高是2,圆锥的底面半径是1,高是2,所以该几何体的体积V=×2×2×2-×π×12×2=。故选B。 答案 B 4.(2018·福建漳州二模)如图,在边长为1的正方形组成的网格中,画出的是一个几何体的三视图,则该几何体的体积是( ) A.9 B. C.18 D.27 解析 根据三视图可知该几何体是一个三棱锥,将三棱锥A-BCD还原到长方体中,长方体的长、宽、高分别为6、3、3,所以该几何体的体积V=××6×3×3=9。故选A。 答案 A 5.(2018·全国卷Ⅰ)已知圆柱的上、下底面的中心分别为O1,O2,过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为( ) A.12π B.12π C.8π D.10π 解析 根据题意,可得截面是边长为2的正方形,所以圆柱的高为2,底面圆的半径为,所以其表面积为S=2π()2+2π×2=12π。故选B。 答案 B 6.(2018·成都诊断)在三棱锥P-ABC中,已知PA⊥底面ABC,∠BAC=60°,PA=2,AB=AC=,若该三棱锥的顶点都在同一个球面上,则该球的表面积为( ) A. B. C.8π D.12π 解析 易知△ABC是等边三角形。如图,作OM⊥平面ABC,其中M为△ABC的中心,且点O满足OM=PA=1,则点O为三棱锥P-ABC外接球的球心。于是,该外接球的半径R=OA===。故该球的表面积S=4πR2=8π。故选C。 答案 C 7.一个正方体被一个平面截去一部分后,剩余部分的三视图如图,则截去部分体积与剩余部分体积的比值为________。 解析 由已知三视图知该几何体是由一个正方体截去了一个“大角”后剩余的部分,如图所示,截去部分是一个三棱锥。设正方体的棱长为1,则三棱锥的体积为V1=××1×1×1=,剩余部分的体积V2=13-=。所以==。 答案 8.(2018·江苏高考)如图所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为________。 解析 正方体的棱长为2,以其所有面的中心为顶点的多面体是正八面体,其中正八面体的所有棱长都是,则该正八面体的体积为×()2×1×2=。 答案 9.如图,在正三棱柱ABC-A1B1C1中,D为棱AA1的中点。若AA1=4,AB=2,则四棱锥B-ACC1D的体积为________。 解析 取AC的中点O,连接BO,则BO⊥AC,所以BO⊥平面ACC1D,因为AB=2,所以BO=,因为D为棱AA1的中点,AA1=4,所以S梯形ACC1D=(2+4)×2=6,所以四棱锥B-ACC1D的体积为2。 答案 2 10.设A,B,C,D是同一个半径为4的球的球面上四点,△ABC为等边三角形且其面积为9,则三棱锥D-ABC体积的最大值为________。 解析 设等边三角形ABC的边长为x,则x2sin60°=9,得x=6。设△ABC的外接圆半径为r,则2r=,解得r=2,所以球心到△ABC所在平面的距离d==2,则点D到平面ABC的最大距离d1=d+4=6,所以三棱锥D-ABC体积的最大值Vmax=S△ABC×6=×9×6=18。 答案 18 11.(2018·河南新乡一模)如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,其中俯视图中的两段圆弧均为半圆,该几何体的体积为( ) A.8-π B.8-π C.8-2π D.8+2π 解析 由三视图可知该几何体是由正方体挖去两个半圆柱后形成的,如图。该几何体的体积为2×2×2-2××π×12×2=8-2π。故选C。 答案 C 12.(2018·全国卷Ⅰ) 已知正方体的棱长为1,每条棱所在直线与平面α所成的角都相等,则α截此正方体所得截面面积的最大值为( ) A. B. C. D. 解析 记该正方体为ABCD-A′B′C′D′,正方体的每条棱所在直线与平面α所成的角都相等,即共点的三条棱A′A,A′B′,A′D′与平面α所成的角都相等。如图,连接AB′,AD′,B′D′,因为三棱锥A′-AB′D′是正三棱锥,所以A′A,A′B′,A′D′与平面AB′D′所成的角都相等。分别取C′D′,B′C′,BB′,AB,AD,DD′的中点E,F,G,H,I,J,连接EF,FG,GH,HI,IJ,JE,易得E,F,G,H,I,J六点共面,平面EFGHIJ与平面AB′D′平行,且截正方体所得截面的面积最大。又EF=FG=GH=HI=IJ=JE=,所以该正六边形的面积为6××2=,所以α截此正方体所得截面面积的最大值为,故选A。 答案 A 13.(2018·东北三校二模)已知某几何体的三视图如图所示,过该几何体最短两条棱的中点作平面α,使得α平分该几何体的体积,则可以作此种平面α( ) A.恰好1个 B.恰好2个 C.至多3个 D.至少4个 解析 几何体的直观图如图所示。该几何体最短两条棱为PA和BC,设PA和BC的中点分别为E,F,则过E,F且平分几何体体积的平面α,可能为:①平面PAF;②平面BCE;③ 平面EGFH(其中G,H为AC和PB的中点);④平面EMFN(其中M,N为PC和AB的中点),所以此种平面至少4个。故选D。 答案 D 14.(2018·江西九江二模)如图,在直三棱柱ABC-A1B1C1中,底面ABC是等腰直角三角形,AB=BC=1。点D为侧棱BB1上的动点。若△ADC1周长的最小值为+,则三棱锥C1-ABC外接球的表面积为________。 解析 将侧面展开如图,易知当D为侧棱BB1的中点时,△ADC1周长最小,此时设BD=x,则2+=+,可得x=,所以CC1=1,又易知三棱锥C1-ABC外接球的球心为AC1的中点,所以半径R=,则三棱锥C1-ABC外接球的表面积为S=4πR2=3π。 答案 3π 15.(2018·长春质量监测)已知圆锥的侧面展开图是半径为3的扇形,则该圆锥体积的最大值为________。 解析 由题意得圆锥的母线长为3,设圆锥的底面半径为r,高为h,则h=,所以圆锥的体积V=πr2h=πr2=π。设f(r)=9r4-r6(r>0),则f′(r)=36r3-6r5,令f′(r)=36r3-6r5=6r3(6-r2)=0,得r=,所以当0查看更多