【数学】2019届一轮复习全国通用版第63讲算法与程序框图学案

【数学】2019届一轮复习全国通用版第63讲算法与程序框图学案

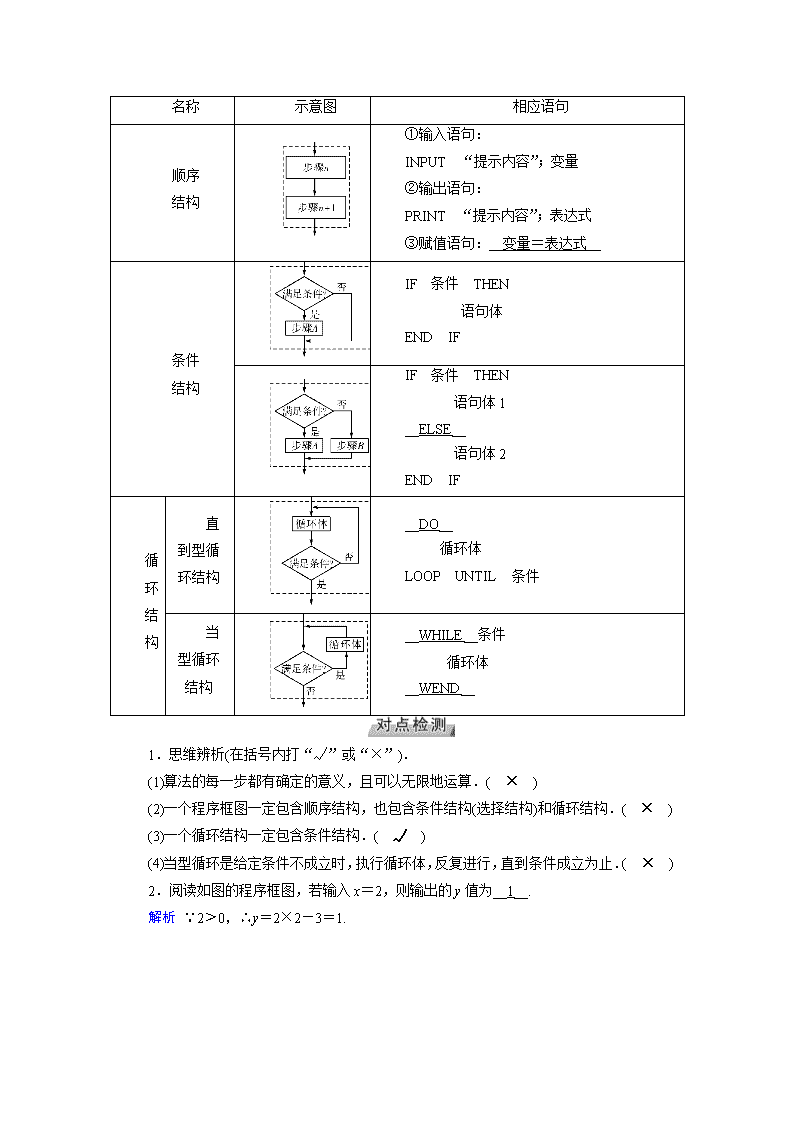
第十章　算法初步、统计、统计案例 第63讲　算法与程序框图 考纲要求 考情分析 命题趋势 ‎1.了解算法的含义，了解算法的思想．‎ ‎2．理解程序框图的三种基本逻辑结构：顺序结构、条件结构、循环结构．‎ ‎3．理解几种基本算法语句——输入语句、输出语句、赋值语句、条件语句、循环语句的含义.‎ ‎2017·全国卷Ⅰ，8‎ ‎2017·全国卷Ⅱ，8‎ ‎2017·山东卷，6‎ ‎2016·全国卷Ⅰ，9‎ ‎2016·全国卷Ⅱ，8‎ 程序框图中的条件分支结构及循环结构是高考对算法考查的主要内容，常与函数求值、方程求解、不等式求解、数列求和、统计量计算等问题交汇命题；给出程序框图的全部或部分，读出其功能，执行该程序框图并求输出结果及补齐框图是高考热点.‎ 分值：5分 ‎1．算法的含义与程序框图 ‎(1)算法：算法是指按照一定规则解决__某一类__问题的明确和__有限的__步骤．‎ ‎(2)程序框图：程序框图又称流程图，是一种用__程序框__、__流程线__及__文字说明__来表示算法的图形．‎ ‎(3)程序框图中图形符号的含义 图形符号 名称 功能 ‎__终端框(起止框)__‎ 表示一个算法的__起始__和__结束__‎ ‎__输入、输出框__‎ 表示一个算法__输入__和__输出__的信息 ‎__处理框(执行框)__‎ 赋值、计算 ‎__判断框__‎ 判断某一条件是否成立，成立时在出口处标明“是”或“Y”；不成立时标明“否”或“N”‎ 流程线 连接程序框 ‎○‎ 连接点 连接程序框图的两部分 ‎2．三种基本逻辑结构及相应语句 名称 示意图 相应语句 顺序 结构 ‎①输入语句：‎ INPUT　“提示内容”；变量 ‎②输出语句：‎ PRINT　“提示内容”；表达式 ‎③赋值语句：__变量＝表达式__‎ 条件 结构 IF　条件　THEN ‎ 语句体 END　IF IF　条件　THEN ‎ 语句体1‎ ‎__ELSE__‎ ‎ 语句体2‎ END　IF 循 环 结 构 直到型循环结构 ‎__DO__‎ ‎ 循环体 LOOP　UNTIL　条件 当型循环结构 ‎__WHILE__条件 ‎ 循环体 ‎__WEND__‎ ‎1．思维辨析(在括号内打“√”或“×”)．‎ ‎(1)算法的每一步都有确定的意义，且可以无限地运算．(　×　)‎ ‎(2)一个程序框图一定包含顺序结构，也包含条件结构(选择结构)和循环结构．(　×　)‎ ‎(3)一个循环结构一定包含条件结构．(　√　)‎ ‎(4)当型循环是给定条件不成立时，执行循环体，反复进行，直到条件成立为止．(　×　)‎ ‎2．阅读如图的程序框图，若输入x＝2，则输出的y值为__1__.‎ 解析 ∵2＞0，∴y＝2×2－3＝1.‎ 第2题图　　　　　　　　　　　第3题图 ‎3．如图所示，程序框图(算法流程图)的输出结果为____.‎ 解析 第一次循环后：s＝0＋，n＝4；第二次循环后：s＝0＋＋，n＝6；第三次循环后：s＝0＋＋＋，n＝8，跳出循环，输出s＝0＋＋＋＝.‎ ‎4．已知函数y＝如图是给定x的值，求其对应的函数值y的程序框图，①处应填写__x<2？__；②处应填写__y＝log2x__.‎ ‎　　 第4题图　　　　　　　　　第5题图 解析 由框图可知只要满足①中的条件则对应的函数解析式为y＝2－x，故此处应填写“x＜2？”，则②处应填写y＝log2x.‎ ‎5．阅读程序：‎ 若x＝－4，输出结果为__负数__，‎ 若x＝9，输出结果为__3__.‎ 解析 该算法程序中使用的是条件语句，根据其特征可得出结果．‎ 一　顺序结构与条件结构 ‎(1)顺序结构：顺序结构是最简单的算法结构，语句与语句之间、框与框之间是按从上到下的顺序进行的．‎ ‎(2)条件结构：利用条件结构解决算法问题时，重点是判断框，判断框内的条件不同，对应的下一图框中的内容和操作要相应地进行变化，故要重点分析判断框内的条件是否满足．　‎ ‎【例1】 (1)根据图(1)的框图，对大于2的整数n，输出的数列的通项公式是(　C　)‎ A．an＝2n　　 B．an＝2(n－1)‎ C．an＝2n　　 D．an＝2n－1‎ ‎(2)运行如图(2)所示的程序框图，输出A，B，C的一组数据为，－1,2，则在两个判断框内的横线上分别应填(　A　)‎ A．垂直、相切　　　　 B．平行、相交 C．垂直、相离　　　　 D．平行、相切 解析 (1)由程序框图可知：a1＝2×1＝2，a2＝2×2＝22，a3＝2×4＝23，a4＝2×8＝24，…归纳可得an＝2n，故选C．‎ ‎(2)顺序执行程序，由输出结果可知，直线Ax＋By＋C＝0应为x－y＋2＝0.根据斜率之间的关系可判断与直线x＋y－1＝0垂直，又点(0,0)到直线x－y＋2＝0的距离d＝＝1＝r.所以直线x－y＋2＝0与圆x2＋y2＝1相切，所以第一个判断框中应是垂直，第二个判断框中应是相切．‎ 二　循环结构 循环结构的常考类型及解题思路 ‎(1)确定循环次数：分析进入或退出循环体的条件，确定循环次数．‎ ‎(2)‎ 完善程序框图：结合初始条件和输出结果，分析控制循环的变量应满足的条件或累加、累乘的变量的表达式．‎ ‎(3)辨析循环功能：执行程序若干次，即可判断．‎ ‎【例2】 (1)(2017·全国卷Ⅱ)执行图(3)的程序框图，如果输入的a＝－1，则输出的S＝(　B　)‎ A．2　　 B．3　　　　‎ C．4　　 D．5‎ ‎ ‎ ‎　　图(3) 图(4)‎ ‎(2)(2017·全国卷Ⅰ)图(4)的程序框图是为了求出满足3n－2n>1 000的最小偶数n，那么在和两个空白框中，可以分别填入(　D　)‎ A．A>1 000和n＝n＋1　　　　‎ B．A>1 000和n＝n＋2‎ C．A≤1 000和n＝n＋1　　　　‎ D．A≤1 000和n＝n＋2‎ 解析 (1)运行程序框图，a＝－1，S＝0，K＝1，K≤6成立；‎ S＝0＋(－1)×1＝－1，a＝1，K＝2，K≤6成立；‎ S＝－1＋1×2＝1，a＝－1，K＝3，K≤6成立；‎ S＝1＋(－1)×3＝－2，a＝1，K＝4，K≤6成立；‎ S＝－2＋1×4＝2，a＝－1，K＝5，K≤6成立；‎ S＝2＋(－1)×5＝－3，a＝1，K＝6，K≤6成立；‎ S＝－3＋1×6＝3，a＝－1，K＝7，K≤6不成立，输出S＝3.‎ ‎(2)程序框图中A＝3n－2n，故判断框中应填入A≤1 000，由于初始值n＝0，要求满足A＝3n－2n>1 000的最小偶数，故执行框中应填入n＝n＋2，故选D．‎ 三　基本算法语句 基本算法语句的两点要求 ‎(1)输入语句的要求 ‎①输入语句要求输入的值是具体的常量；‎ ‎②提示内容提示用户输入的是什么信息，必须加双引号，提示内容“原原本本”地在计算机屏幕上显示，提示内容与变量之间要用分号隔开．‎ ‎(2)输出语句的要求 ‎①表达式是算法和程序要求输出的信息；‎ ‎②提示内容提示用户要输出的是什么信息，必须加双引号，提示内容和表达式要用分号分开．‎ ‎(3)输出语句可以一次完成输出多个表达式的功能，不同的表达式之间可用“，”分隔；输出语句还可以是“提示内容‎1”‎；表达式1，“提示内容‎2”‎；表达式2，“提示内容‎3”‎；表达式3，……的形式，例如，PRINT“a，b，c”；a，b，c和PRINT“a”；a，“b”；b，“c”；c.‎ ‎【例3】 (1)执行图(5)的算法语句，当输入x为60时，输出y的值为(　C　)‎ A．25　　 B．30　　　　‎ C．31　　 D．61‎ ‎(2)设计一个计算1×3×5×7×9×11×13的算法，如图(6)给出了程序的一部分，则在①处不能填入的数是(　A　)‎ A．13　　 B．13.5‎ C．14　　 D．14.5‎ 解析 (1)该语句表示分段函数y＝ ‎ 当x＝60时，y＝25＋0.6×(60－50)＝31.‎ ‎∴输出y的值为31.‎ ‎(2)若填13，当i＝11＋2＝13时，不满足条件，终止循环，因此得到的是1×3×5×7×9×11的计算结果，故不能填13，但填的数字只要超过13且不超过15均可保证终止循环时，得到的是1×3×5×7×9×11×13的计算结果．‎ 四　算法案例 ‎(1)‎ 更相减损术和辗转相除法能求出两个正数的最大公约数，但后者比前者简单，了解这两种方法，能对中国古代数学与世界数学的发展进行比较．‎ ‎(2)秦九韶算法是中国古代在计算多项式值方面的优秀方法，在应用时要注意以下几点：‎ ‎①正确改写多项式(降幂排列)；②计算应由内向外依次计算；③当多项式函数中间出现空项式，要以系数为零的齐次项补充．‎ ‎(3)数的进制转换是算法案例之一，是计算机语言的基础．‎ ‎【例4】 (1)3743(8)＝__2_019__(十进制数)＝__11111100011__(二进制数)．‎ ‎(2)用辗转相除法求得378和90的最大公约数为__18__；用更相减损术求得80和36的最大公约数为__4__.‎ ‎(3)用秦九韶算法求多项式f(x)＝3x6＋12x5＋8x4－3.5x3＋7.2x2＋5x－13，则f(6)＝__243_168.2__.‎ 解析 (1)3743(8)＝3×83＋7×82＋4×8＋3＝2 019，‎ ‎2 019＝210＋29＋28＋27＋26＋25＋2＋1＝11111100011(2)．‎ ‎(2)∵378＝90×4＋18,90＝18×5＋0，‎ ‎∴378与90的最大公约数是18.‎ ‎∵80－36＝44,44－36＝8,36－8＝28,28－8＝20,20－8＝12,12－8＝4,8－4＝4,4－4＝0，‎ ‎∴80和36的最大公约数是4.‎ ‎(3)f(x)＝(((((3x＋12)x＋8)x－3.5)x＋7.2)x＋5)x－13，‎ v0＝3，v1＝3×6＋12＝30，‎ v2＝v1x＋8＝30×6＋8＝188，‎ v3＝v2x－3.5＝188×6－3.5＝1 124.5，‎ v4＝v3x＋7.2＝1 124.5×6＋7.2＝6 754.2，‎ v5＝v4x＋5＝6 754.2×6＋5＝40 530.2，‎ v6＝v5x－13＝40 530.2×6－13＝243 168.2，‎ ‎∴f(6)＝243 168.2.‎ ‎1．(2017·山东卷)执行两次下图所示的程序框图，若第一次输入的x的值为7，第二次输入的x的值为9，则第一次、第二次输出的a的值分别为(　D　)‎ A．0,0　　 B．1,1　　　　‎ C．0,1　　 D．1,0‎ 解析 当输入x＝7时，b＝2，因为b2>x不成立，且x不能被b整除，故b＝3，这时b2>x成立，故a＝1，输出a的值为1.当输入x＝9时，b＝2，因为b2>x不成立，且x不能被b整除，故b＝3，这时b2>x不成立且x能被b整除，故a＝0，输出a的值为0.‎ ‎2．(2016·全国卷Ⅰ)执行下面的程序框图，如果输入的x＝0，y＝1，n＝1，则输出x，y的值满足(　C　)‎ A．y＝2x　　 B．y＝3x　　‎ C．y＝4x　　 D．y＝5x 解析 x＝0，y＝1，n＝1；x＝0，y＝1，n＝2；x＝，y＝2，n＝3；x＝，y＝6，此时x2＋y2＞36，输出x＝，y＝6，满足y＝4x，故选C．‎ ‎3．如图，程序执行后输出的结果是__990__.‎ 解析 程序反映出的算法过程为 i＝11⇒S＝11×1，i＝10；‎ i＝10⇒S＝11×10，i＝9；‎ i＝9⇒S＝11×10×9，i＝8；‎ i＝8<9退出循环，执行“PRINT　S”．‎ 故S＝990.‎ ‎4．用秦九韶算法求多项式f(x)＝8x7＋5x6＋3x4＋2x＋1，则f(2)＝__1_397__.‎ 解析 根据秦九韶算法，把多项式改写成如下形式：‎ f(x)＝8x7＋5x6＋0·x5＋3·x4＋0·x3＋0·x2＋2x＋1‎ ‎＝((((((8x＋5)x＋0)x＋3)x＋0)x＋0)x＋2)x＋1.‎ 而x＝2，所以有v0＝8，‎ v1＝8×2＋5＝21，‎ v2＝21×2＋0＝42，‎ v3＝42×2＋3＝87，‎ v4＝87×2＋0＝174，‎ v5＝174×2＋0＝348，‎ v6＝348×2＋2＝698，‎ v7＝698×2＋1＝1 397.‎ 所以当x＝2时，f(2)＝1 397.‎ 易错点　对循环结构认识不清晰 错因分析：执行循环结构时，当判断框中的条件满足时执行循环．当判断框中的条件不满足时结束循环，并判断输出结果是否正确．‎ ‎【例1】 如下图所示是一算法的程序框图，若此程序运行结果为S＝720，则在判断框中应填入关于k的判断条件是(　　)‎ A．k≥6？　　 B．k≥7？　　　　‎ C．k≥8？　　 D．k≥9?‎ 解析 第一次运行结果为S＝10，k＝9；第二次运行结果为S＝10×9＝90，k＝8；第三次运行结果为S＝720，k＝7.这个程序满足判断框的条件时执行循环，故判断框中填“k≥8？”．‎ 答案 C ‎【跟踪训练1】 执行如下图所示程序框图，若输出的S值为－52，则条件框内应填写(　B　)‎ A．i<4？　　 B．i<6?‎ C．i<5？　　 D．i>5?‎ 解析 第一次循环：S＝10－2＝8，i＝2；‎ 第二次循环：S＝4，i＝3；第三次循环：S＝－4，i＝4；‎ 第四次循环：S＝－20，i＝5；第五次循环：S＝－52，i＝6；‎ 结束循环，∴应填写i<6？.‎ 课时达标　第63讲 ‎[解密考纲]算法与程序框图在高考中常以选择题、填空题的形式出现．‎ 一、选择题 ‎1．(2017·天津卷)阅读如图所示的程序框图，运行相应的程序，若输入N的值为24，则输出N的值为(　C　)‎ A．0　　 B．‎1　‎　‎ C．2　　 D．3‎ 解析 第一次循环，24能被3整除，N＝＝8>3；第二次循环，8不能被3整除，N＝8－1＝7>3；第三次循环，7不能被3整除，N＝7－1＝6>3；第四次循环，6能被3整除，N＝＝2<3，结束循环，故输出N的值为2，故选C． ‎ ‎2．执行如图所示的框图，若输入的N是6，则输出的p的值是(　B　)‎ A．120　　 B．720　　　　‎ C．1 440　　 D．5 040‎ 解析 第一次循环：p＝1，k＝2；第二次循环：p＝2，k＝3；第三次循环：p＝6，k＝4；第四次循环：p＝24，k＝5；第五次循环：p＝120，k＝6；第六次循环：p＝720.此时条件不成立，输出720，故选B．‎ ‎3．执行如图所示的程序框图，则输出的结果是(　C　)‎ A．14　　 B．15　　　　‎ C．16　　 D．17‎ 解析 由程序框图可知，从n＝1到n＝13，S＝0＋log2＋log2＋…＋log2＝log2>－3；当n＝14时，执行循环，得S＝－3，n＝14＋1＝15，继续进行循环，得S＝－3＋log2，n＝15＋1＝16，满足条件，结束循环，输出16，故选C．‎ ‎4．给出一个程序框图如图，则输出x的值是(　C　)‎ A．39　　 B．41　　　　‎ C．43　　 D．45‎ 解析 由程序框图可知，S＝5＋7＋9＋…＋2n＋3，只要S<480，就再一次进入循环体循环，直到首次出现S≥480，才跳出循环体，输出x，程序运行结束．由S＝5＋7＋9＋…＋2n＋3＝n2＋4n≥480，得n≥20，所以x＝2×20＋3＝43.‎ ‎5．(2017·全国卷Ⅲ)执行图的程序框图，为使输出S的值小于91，则输入的正整数N的最小值为(　D　)‎ A．5　　 B．4　　　　‎ C．3　　 D．2‎ 解析 S＝0＋100＝100，M＝－10，t＝2,100>91；S＝100－10＝90，M＝1，t＝3,90<91，输出S，此时，t＝3不满足t≤N，所以输入正整数N的最小值为2，故选D．‎ ‎6．(2016·全国卷Ⅱ)中国古代有计算多项式值的秦九韶算法，如图是实现该算法的程序框图．执行该程序框图，若输入的x＝2，n＝2，依次输入的a为2,2,5，则输出的s＝(　C　)‎ A．7　　 B．12　　　　‎ C．17　　 D．34‎ 解析 由程序框图知，第一次循环：x＝2，n＝2，a＝2，s＝0×2＋2＝2，k＝1；第二次循环：a＝2，s＝2×2＋2＝6，k＝2；第三次循环：a＝5，s＝6×2＋5＝17，k＝3.结束循环，输出s的值为17，故选C．‎ ‎7．如图所示，程序框图(算法流程图)的输出结果是(　D　)‎ A．　　 B．　　　　‎ C．　　 D． 解析 2<8，s＝0＋＝，n＝2＋2＝4；4<8，s＝＋＝，‎ n＝4＋2＝6；6<8，s＝＋＝，n＝6＋2＝8.由8<8 不成立，可知输出.‎ ‎8．某程序框图如图所示，若该程序运行后输出的值是，则(　A　)‎ A．a＝4　　 B．a＝5‎ C．a＝6　　 D．a＝7‎ 解析 该程序框图的功能为计算1＋＋＋…＋＝2－的值，由已知输出的值为，可得2－＝，解得a＝4.　‎ 二、填空题 ‎9．如图(1)是某县参加2017年高考的学生身高条形统计图，从左到右的各条形表示的学生人数依次记为A1，A2，…，A10(如A2表示身高(单位：cm)在[150,155)内的学生人数)．图(2)是统计图(1)中身高在一定范围内学生人数的一个程序框图．现要统计身高在160～‎180 cm(含‎160 cm，不含‎180 cm)的学生人数，则在流程图中的判断框内应填写__i<8？(或i≤7？)__．　‎ ‎　‎ 图(1)　　　　　　　　　　　　图(2)‎ 解析 统计身高在160～180 cm的学生人数，即求A4＋A5＋A6＋A7的值．当4≤i≤7时，符合要求．‎ ‎10．执行如图所示的程序框图，输出的S的值为__4__.‎ 解析 i＝1，S＝＝－1；i＝2，S＝＝；‎ i＝3，S＝＝；i＝4，S＝＝4；‎ i＝5，S＝＝ －1.‎ 所以S的取值具有周期性，周期为4.由i＋1≥2 017，得i≥2 016.所以当i＝2 016时，输出S，此时i＝2 016＝504 ×4，所以输出S的值和i＝4时S的值相同，所以输出的S的值为4.‎ ‎11．已知数列{an}中，a1＝1，an＋1＝an＋n，利用如图所示的程序框图输出该数列的第10项，则判断框中应填的语句是n<__10__(填一个整数值)．‎ 解析 循环开始前：n＝1，m＝1；循环1次：m＝2，n＝2；循环2次：m＝4，n＝3，…；循环9次：n＝10，循环结束，输出结果，故n<10.‎ ‎12．(2017·江苏卷)如图是一个算法流程图，若输入x的值为，则输出y的值是__－2__.‎ 解析 由流程图可得y＝所以当输入的x的值为时，y＝2＋log2＝2－4＝－2.‎